2.5.2 利用函数的图象解一元二次方程课件
文档属性
| 名称 | 2.5.2 利用函数的图象解一元二次方程课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:08:51 | ||
图片预览






文档简介
课件26张PPT。第二章 二次函数第5节 二次函数与一元二次方程第2课时 利用函数的图象解
一元二次方程1课堂讲解利用函数的图象解一元二次方程
利用二次函数的图象解一元一次不等式2课时流程逐点
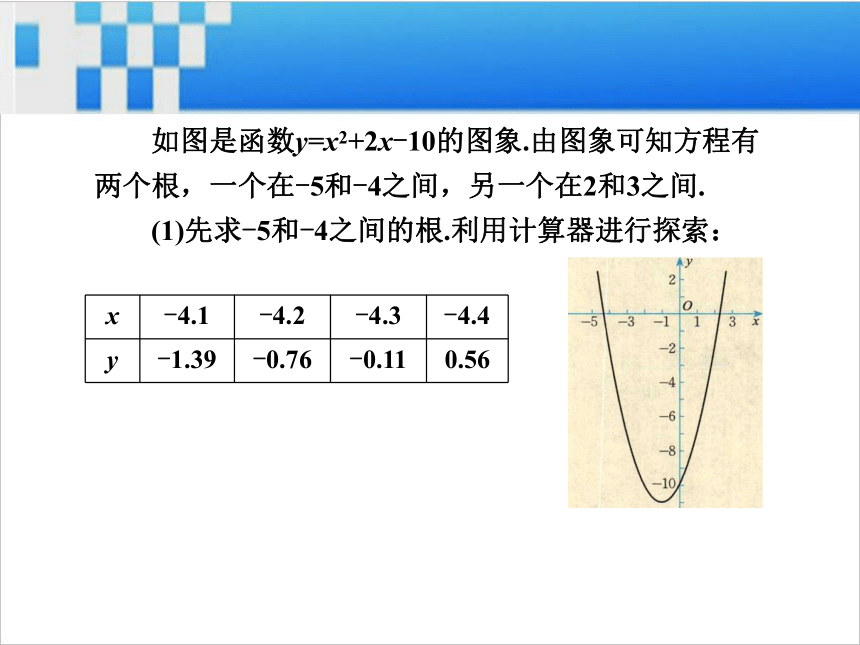
导讲练课堂小结作业提升 你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗? 如图是函数y=x2+2x-10的图象.由图象可知方程有
两个根,一个在-5和-4之间,另一个在2和3之间.
(1)先求-5和-4之间的根.利用计算器进行探索:
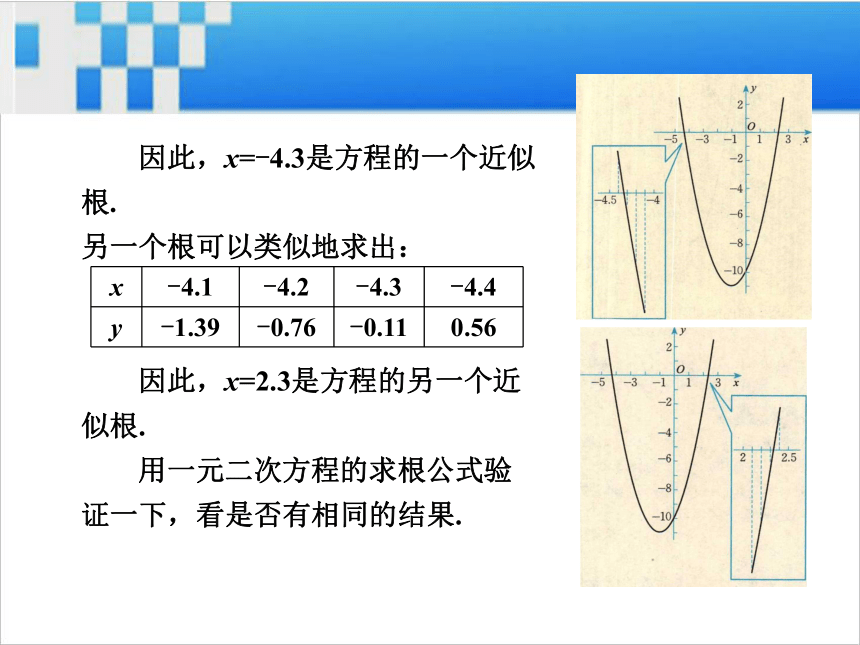
因此,x=-4.3是方程的一个近似
根.
另一个根可以类似地求出:
因此,x=2.3是方程的另一个近
似根.
用一元二次方程的求根公式验
证一下,看是否有相同的结果.1知识点利用二次函数的图象解一元二次方程1.利用二次函数的图象求一元二次方程的近似根的一般步骤:
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在
哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,
当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>
0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较
|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,
则x2是方程的近似根.知1-讲2.利用图象交点法求一元二次方程ax2+bx+c=0的根的步骤:
(1)将方程化为ax2=-bx-c(或x2= )的形式.
(2)在同一平面直角坐标系中画出抛物线y=ax2与直线y=-bx
-c.
(3)观察图象,①若抛物线与直线无公共点,则一元二次方程
ax2+bx+c=0无实根;②若抛物线与直线只有一个公共点,
则一元二次方程ax2+bx+c=0有两个相等的实数根,公共
点的横坐标即为方程的实数根;若抛物线与直线有两个公
共点,则一元二次方程ax2+bx+c=0有两个不相等的实数
根,公共点的横坐标即为方程的实数根.知1-讲导引:当 y=-x2+2x-3的函数值为-8时,对应点的横
坐标即为一元二次方程-x2+2x-3=-8的根,如
图所示.例1 利用二次函数的图象求一元二次方程-x2+2x-
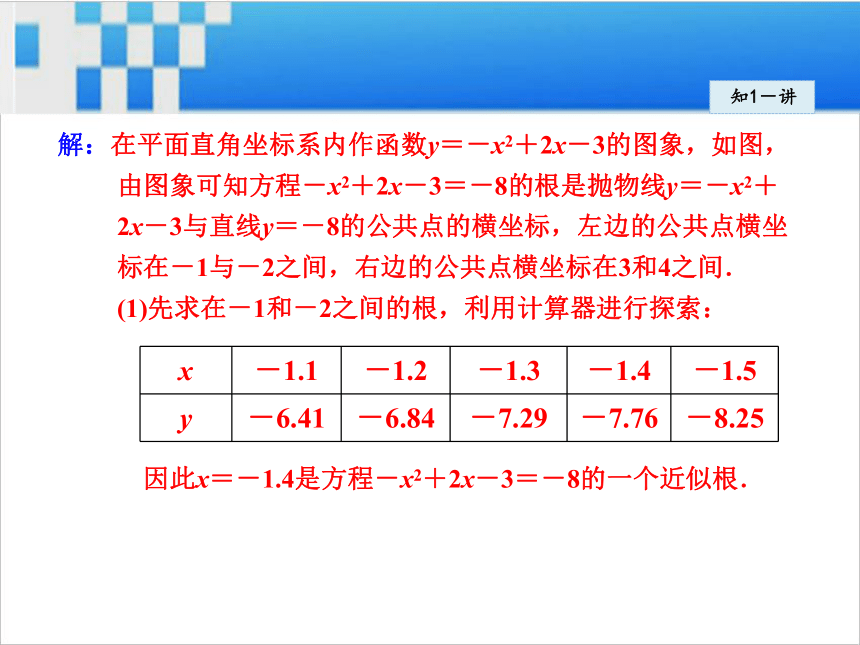
3=-8的近似根.知1-讲解:在平面直角坐标系内作函数y=-x2+2x-3的图象,如图,
由图象可知方程-x2+2x-3=-8的根是抛物线y=-x2+
2x-3与直线y=-8的公共点的横坐标,左边的公共点横坐
标在-1与-2之间,右边的公共点横坐标在3和4之间.
(1)先求在-1和-2之间的根,利用计算器进行探索:
因此x=-1.4是方程-x2+2x-3=-8的一个近似根.
知1-讲(2)另一根可以类似地求出:
因此x=3.4是方程-x2+2x-3=-8的另一个近似根.知1-讲解:先把方程化成x2=-2x+3.
如图,在同一直角坐标系中
分别画出函数y=x2和
y=-2x+3的图象,得到它
们的交点为(-3,9)和(1,1),
则方程x2+2x-3=0的解为x=-3或x=1.例2 利用函数的图象,求方程x2+2x-3=0的根.知1-讲知1-讲 利用图象交点法求一元二次方程的根的步骤:
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情
况,如有公共点,则公共点的横坐标即为ax2+bx+
c=0的根.?1 二次函数y=ax2+bx+c的图象如图所示,则一元二
次方程ax2+bx+c=0的两根为( )
A.x1=1,x2=-3
B.x1=x2=-1
C.x1=x2=3
D.x1=-1,x2=3知1-练2 如图是二次函数y=ax2+bx+c的图象,图象上有两点
分别为A(2.18,-0.61),B(2.68,0.44),则方程ax2+
bx+c=0的一个解只可能是( )
A.2.18
B.2.68
C.-0.51
D.2.55知1-练3 根据下面表格的对应值,判断方程ax2+bx+c=0
(a≠0,a,b,c为常数)一个解x的范围是( )
A. 3<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26知1-练2知识点利用二次函数的图象解一元二次不等式知2-讲 根据图象可直观地回答使得y的值大于、等于或小
于零时x的取值(范围),具体如下表所述:知2-讲例3 画出抛物线y=-x2+4x+5,观察抛物线,回答下
列问题:
(1)x为何值时,函数值y>0?
(2)x为何值时,函数值y=0?
(3)x为何值时,函数值y<0?导引:根据抛物线的简易画法,先确定顶点以及抛物线与x
轴和y轴的交点,当函数值y>0时,对应图象上的点
在x轴上方;当函数值y=0时,对应图象上的点位于
x轴上;当函数值y<0时,对应图象上的点在x轴的
下方.知2-讲解:∵y=-x2+4x+5=-(x2-4x)+5=-(x2-4x+4)+9=
-(x-2)2+9.∴抛物线的顶点坐标
为(2,9),对称轴为直线x=2.
令-x2+4x+5=0,即x2-4x-5=
0,∴x1=5,x2=-1.∴抛物线与x
轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y轴的
交点为(0,5).由抛物线的对称性知抛物线上的另一点为
(4,5).在坐标系中描出各点,并连线得到如图所示的图
象.观察图象会发现:(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值y=0;
(3)当x<-1或x>5时,函数值y<0知2-讲(1)作抛物线y=ax2+bx+c(b2-4ac>0)一般采用“五点法”,
而这“五点”一般为抛物线顶点,与x轴的两交点,与y
轴的交点及它关于对称轴的对称点.
(2)根据二次函数值的取值范围确定自变量的取值范围,
一般要画出二次函数的图象,观察图象解答,抛物线
在x轴上方的部分,对应的函数值大于0;抛物线在x
轴下方的部分,对应的函数值小于0;抛物线与x轴的
公共点,对应的函数值等于0.知2-讲例4 〈齐齐哈尔〉抛物线y=ax2+bx+c(a≠0)的对称轴
为直线x=-1,与x轴的一个交点A在(-3,0)和
(-2,0)之间,其部分图象如图所示,则下列结
论:①4ac-b2<0;②2a-b=0;③a+b+c<0;
④点M(x1,y1),N(x2,y2)在抛物线上,若x1<x2,
则y1<y2.正确结论
的个数是( )
A.1 B.2
C.3 D.4C知2-讲导引:观察图象可知二次函数对应的一元二次方程有两个
不相等的实数解,所以Δ=b2-4ac>0,即4ac-b2<
0,故①正确;因为抛物线的对称轴为直线x=-1,
所以- =-1,即b=2a,2a-b=0,故②正确;
由二次函数图象的对称性可知抛物线与x轴的另一
个交点位于(0,0)和(1,0)之间,所以当x=1时,y
<0,即a+b+c<0,故③正确;由于二次函数在对
称轴两侧的增减性不一样,当x1 当-1y2;当x1<-1<x2且-1-x1=
x2-(-1)时,y1=y2,所以④错误.所以此题正
确的结论有3个.故选C.知2-讲 对于抛物线y=ax2+bx+c(bc≠0),a决定抛物线的开口
方向,当a>0时抛物线开口向上,当a<0时抛物线开口向下;
a,b共同决定对称轴位置,当a,b同号时,对称轴在y轴左
侧;当a,b异号时,对称轴在y轴右侧;c为抛物线与y轴交
点的纵坐标,当c>0时,抛物线与y轴交于正半轴(x轴上方),
当c<0时,抛物线与y轴交于负半轴(x轴下方).b2-4ac的符
号决定抛物线与x轴交点的个数,当b2-4ac>0时,抛物线
与x轴有两个交点;当b2-4ac=0时,抛物线与x轴有唯一
一个交点;当b2-4ac<0时,抛物线与x轴没有交点.1 (中考·牡丹江)抛物线y=ax2+bx+c(a<0)如图,则
关于x的不等式ax2+bx+c>0的解集是( )
A.x<2
B.x>-3
C.-3 D.x<-3或x>1知2-练2 (2015·咸宁)如图是二次函数y=ax2+bx+c的图象.
下列结论:①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;③一元二次方程ax2+bx+c=1
的两根之和为-1;④使y≤3成立的x的取值范围是
x≥0.其中正确的有( )
A.1个
B.2个
C.3个
D.4个知2-练 利用图象求一元二次方程的根的方法:直接画出二
次函数y=ax2+bx+c的图象,则图象与x轴交点的横坐
标就是一元二次方程ax2+bx+c=0的根.其步骤一般为
(1)作出二次函数y=ax2+bx+c的图象;
(2)观察图象与x轴交点的个数;
(3)若图象与x轴有交点,估计出图象与x轴交点的横坐标
即可得到一元二次方程的近似根.
一元二次方程1课堂讲解利用函数的图象解一元二次方程
利用二次函数的图象解一元一次不等式2课时流程逐点
导讲练课堂小结作业提升 你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗? 如图是函数y=x2+2x-10的图象.由图象可知方程有
两个根,一个在-5和-4之间,另一个在2和3之间.
(1)先求-5和-4之间的根.利用计算器进行探索:
因此,x=-4.3是方程的一个近似
根.
另一个根可以类似地求出:
因此,x=2.3是方程的另一个近
似根.
用一元二次方程的求根公式验
证一下,看是否有相同的结果.1知识点利用二次函数的图象解一元二次方程1.利用二次函数的图象求一元二次方程的近似根的一般步骤:
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在
哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,
当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>
0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较
|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,
则x2是方程的近似根.知1-讲2.利用图象交点法求一元二次方程ax2+bx+c=0的根的步骤:
(1)将方程化为ax2=-bx-c(或x2= )的形式.
(2)在同一平面直角坐标系中画出抛物线y=ax2与直线y=-bx
-c.
(3)观察图象,①若抛物线与直线无公共点,则一元二次方程
ax2+bx+c=0无实根;②若抛物线与直线只有一个公共点,
则一元二次方程ax2+bx+c=0有两个相等的实数根,公共
点的横坐标即为方程的实数根;若抛物线与直线有两个公
共点,则一元二次方程ax2+bx+c=0有两个不相等的实数
根,公共点的横坐标即为方程的实数根.知1-讲导引:当 y=-x2+2x-3的函数值为-8时,对应点的横
坐标即为一元二次方程-x2+2x-3=-8的根,如
图所示.例1 利用二次函数的图象求一元二次方程-x2+2x-
3=-8的近似根.知1-讲解:在平面直角坐标系内作函数y=-x2+2x-3的图象,如图,
由图象可知方程-x2+2x-3=-8的根是抛物线y=-x2+
2x-3与直线y=-8的公共点的横坐标,左边的公共点横坐
标在-1与-2之间,右边的公共点横坐标在3和4之间.
(1)先求在-1和-2之间的根,利用计算器进行探索:
因此x=-1.4是方程-x2+2x-3=-8的一个近似根.
知1-讲(2)另一根可以类似地求出:
因此x=3.4是方程-x2+2x-3=-8的另一个近似根.知1-讲解:先把方程化成x2=-2x+3.
如图,在同一直角坐标系中
分别画出函数y=x2和
y=-2x+3的图象,得到它
们的交点为(-3,9)和(1,1),
则方程x2+2x-3=0的解为x=-3或x=1.例2 利用函数的图象,求方程x2+2x-3=0的根.知1-讲知1-讲 利用图象交点法求一元二次方程的根的步骤:
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情
况,如有公共点,则公共点的横坐标即为ax2+bx+
c=0的根.?1 二次函数y=ax2+bx+c的图象如图所示,则一元二
次方程ax2+bx+c=0的两根为( )
A.x1=1,x2=-3
B.x1=x2=-1
C.x1=x2=3
D.x1=-1,x2=3知1-练2 如图是二次函数y=ax2+bx+c的图象,图象上有两点
分别为A(2.18,-0.61),B(2.68,0.44),则方程ax2+
bx+c=0的一个解只可能是( )
A.2.18
B.2.68
C.-0.51
D.2.55知1-练3 根据下面表格的对应值,判断方程ax2+bx+c=0
(a≠0,a,b,c为常数)一个解x的范围是( )
A. 3<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26知1-练2知识点利用二次函数的图象解一元二次不等式知2-讲 根据图象可直观地回答使得y的值大于、等于或小
于零时x的取值(范围),具体如下表所述:知2-讲例3 画出抛物线y=-x2+4x+5,观察抛物线,回答下
列问题:
(1)x为何值时,函数值y>0?
(2)x为何值时,函数值y=0?
(3)x为何值时,函数值y<0?导引:根据抛物线的简易画法,先确定顶点以及抛物线与x
轴和y轴的交点,当函数值y>0时,对应图象上的点
在x轴上方;当函数值y=0时,对应图象上的点位于
x轴上;当函数值y<0时,对应图象上的点在x轴的
下方.知2-讲解:∵y=-x2+4x+5=-(x2-4x)+5=-(x2-4x+4)+9=
-(x-2)2+9.∴抛物线的顶点坐标
为(2,9),对称轴为直线x=2.
令-x2+4x+5=0,即x2-4x-5=
0,∴x1=5,x2=-1.∴抛物线与x
轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y轴的
交点为(0,5).由抛物线的对称性知抛物线上的另一点为
(4,5).在坐标系中描出各点,并连线得到如图所示的图
象.观察图象会发现:(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值y=0;
(3)当x<-1或x>5时,函数值y<0知2-讲(1)作抛物线y=ax2+bx+c(b2-4ac>0)一般采用“五点法”,
而这“五点”一般为抛物线顶点,与x轴的两交点,与y
轴的交点及它关于对称轴的对称点.
(2)根据二次函数值的取值范围确定自变量的取值范围,
一般要画出二次函数的图象,观察图象解答,抛物线
在x轴上方的部分,对应的函数值大于0;抛物线在x
轴下方的部分,对应的函数值小于0;抛物线与x轴的
公共点,对应的函数值等于0.知2-讲例4 〈齐齐哈尔〉抛物线y=ax2+bx+c(a≠0)的对称轴
为直线x=-1,与x轴的一个交点A在(-3,0)和
(-2,0)之间,其部分图象如图所示,则下列结
论:①4ac-b2<0;②2a-b=0;③a+b+c<0;
④点M(x1,y1),N(x2,y2)在抛物线上,若x1<x2,
则y1<y2.正确结论
的个数是( )
A.1 B.2
C.3 D.4C知2-讲导引:观察图象可知二次函数对应的一元二次方程有两个
不相等的实数解,所以Δ=b2-4ac>0,即4ac-b2<
0,故①正确;因为抛物线的对称轴为直线x=-1,
所以- =-1,即b=2a,2a-b=0,故②正确;
由二次函数图象的对称性可知抛物线与x轴的另一
个交点位于(0,0)和(1,0)之间,所以当x=1时,y
<0,即a+b+c<0,故③正确;由于二次函数在对
称轴两侧的增减性不一样,当x1
x2-(-1)时,y1=y2,所以④错误.所以此题正
确的结论有3个.故选C.知2-讲 对于抛物线y=ax2+bx+c(bc≠0),a决定抛物线的开口
方向,当a>0时抛物线开口向上,当a<0时抛物线开口向下;
a,b共同决定对称轴位置,当a,b同号时,对称轴在y轴左
侧;当a,b异号时,对称轴在y轴右侧;c为抛物线与y轴交
点的纵坐标,当c>0时,抛物线与y轴交于正半轴(x轴上方),
当c<0时,抛物线与y轴交于负半轴(x轴下方).b2-4ac的符
号决定抛物线与x轴交点的个数,当b2-4ac>0时,抛物线
与x轴有两个交点;当b2-4ac=0时,抛物线与x轴有唯一
一个交点;当b2-4ac<0时,抛物线与x轴没有交点.1 (中考·牡丹江)抛物线y=ax2+bx+c(a<0)如图,则
关于x的不等式ax2+bx+c>0的解集是( )
A.x<2
B.x>-3
C.-3
下列结论:①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;③一元二次方程ax2+bx+c=1
的两根之和为-1;④使y≤3成立的x的取值范围是
x≥0.其中正确的有( )
A.1个
B.2个
C.3个
D.4个知2-练 利用图象求一元二次方程的根的方法:直接画出二
次函数y=ax2+bx+c的图象,则图象与x轴交点的横坐
标就是一元二次方程ax2+bx+c=0的根.其步骤一般为
(1)作出二次函数y=ax2+bx+c的图象;
(2)观察图象与x轴交点的个数;
(3)若图象与x轴有交点,估计出图象与x轴交点的横坐标
即可得到一元二次方程的近似根.
