3.1.2 圆的半径的应用课件
图片预览








文档简介
课件21张PPT。第三章 圆3.1 圆第2课时 圆的半径的应用1课堂讲解同圆的半径相等
点与圆的位置关系
利用圆的半径解决实际问题2课时流程逐点
导讲练课堂小结作业提升1.什么是圆?
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等,到圆心的距离等于半径
的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它
的另一个端点的运动轨迹就是一个圆.
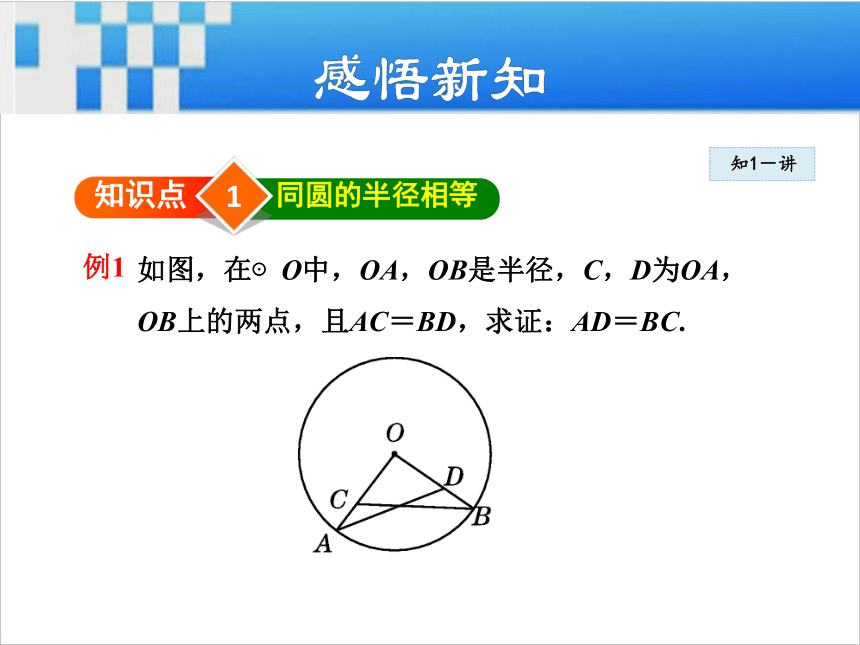
2.点与圆的位置关系有哪些?如何判断?1知识点同圆的半径相等知1-讲如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两点,且AC=BD,求证:AD=BC. 例1知1-讲要证AD=BC,需证其所在的三角形全等,即需证
△ADO≌△BCO.导引:∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OC=OD.
在△ADO和△BCO中,
∴△ADO≌△BCO.
∴AD=BC.证明:知1-讲(1)本例中的OA=OB,即“圆的半径相等”,在以后的
证明中,可直接应用.
(2)“同圆的半径相等”在证明圆中线段相等时有着广泛
应用,应熟练掌握. ,知1-讲如图, AB为⊙O的直径, 点C, D在⊙O上, 已知∠BOC
=70°,AD∥OC,则∠AOD=________. 例2∵AD∥OC,
∴∠DAO=∠BOC=70°.
又∵OA=OD,
∴∠ADO=∠DAO=70°.
∴∠AOD=180°-∠ADO-∠DAO=40°.导引:40°知1-讲本题利用同圆中的半径相等求相关角的度数.如图,AB是⊙O的弦,半径OC,OD分别交AB于点
E,F,且AE=BF,请你判断线段OE与OF的数量
关系,并说明理由.知1-练如图,CD是⊙O的直径,点A在DC的延长线上,∠A
=20°,AE交⊙O于点B,且AB=OC.求:
(1)∠AOB的度数;
(2)∠EOD的度数.知1-练2知识点点与圆的位置关系知2-讲平面上有⊙O及一点P,点P到⊙O上一点的距离最大
为6 cm,最小为2 cm,则⊙O的半径为____________. 例3解答此题应进行分类讨论,点P可能位于圆的内部,
也可能位于圆的外部.当点P在圆内时,直径=6+2
=8(cm),因而半径是4 cm;当点P在圆外时,直径
=6-2=4(cm),因而半径是2 cm.所以⊙O的半径为
4 cm或2 cm.导引:4 cm或2 cm知2-讲 涉及点与圆的位置关系的最值问题,关键是要
运用分类讨论思想,其次是理解最大距离和最小距
离的意义.知2-讲如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.
(1)以点C为圆心,6为半径作圆,
试判断点A,D,B与 圆C的位置关系;
(2)当圆C的半径为多少时,点O在圆C上?
(3)若以点C为圆心作圆,使A,O,B三点至少有一点在圆内,至少有一点在圆外,则圆C的半径r的取值范围是什么?(直接写出答案) 例4知2-讲将点到圆心的距离d与半径r进行比较,当d<r时,点在圆内;
当d=r时,点在圆上;当d>r时,点在圆外.导引:(1)在Rt△ABC中,∠ACB=90°,AB=10,BC=8,
由勾股定理得AC=6=r,所以点A在圆C上.
由S△ACB= CD·AB= AC·BC,
得CD=4.8<6=r,所以点D在圆C内.
又因为BC=8>6=r,所以点B在圆C外.
(2)如图,连接CO,在Rt△ABC中,O为斜边AB的中点,所以
CO= AB= ×10=5,所以当圆C的半径为5时,点O
在圆C上.
(3)半径r的取值范围是5<r<8.解:知2-讲 判断点与圆的位置关系的实质就是将圆心和此点
连线的长度与半径进行比较,点与圆的位置关系的数
量特征是我们判断点与圆的位置关系的重要依据.如图,在△ABC中,∠ACB=90°,AB=10,BC
=8,CD⊥AB于D,O为AB的中点.
(1)以C为圆心,6为半径作圆,
试判断点A,D,B与⊙C的位置关系;
(2)当⊙C的半径为多少时,点O在⊙C上?
(3)若以点C为圆心作圆,使A,O,B三点至少有一点在圆内,至少有一点在圆外,则⊙C的半径r的取值范围是什么?知2-练知3-讲3知识点利用圆的半径解决实际问题 如图,有两条公路OM,ON相交成30°
角,沿公路OM方向离两条公路的交叉
处O点80 m的A处有一所学校,当拖拉
机沿ON方向行驶时,距拖拉机50 m范围内会受到噪音影响,已知有两台相距30 m的拖拉机正沿ON方向行驶,它们的速度均为5 m/s,则这两台拖拉机沿ON方向行驶时给学校带来噪音影响的时间是多少? 例5知3-讲如图,过点A作AC⊥ON,垂足为C.
∵∠MON=30°,OA=80 m,∴AC=40 m.
设第一台拖拉机到B点时开始对学校产生噪音影响,连接
AB,此时AB=50 m,由勾股定理得BC=30 m,
设第一台拖拉机到D点时噪音消失,连接AD,此时AD=50 m,
∴CD=30 m.解:知3-讲由于两台拖拉机相距30 m,
∴第一台到D点时第二台在C点,还需前行30 m后才对学校没
有噪音影响,
∴影响时间应是90÷5=18(s).
答:这两台拖拉机沿ON方向行驶时给学校带来噪音影响的时
间是18 s.知3-练如图,海军某部队在灯塔A周围进行爆破作业,灯塔A的周围3 km的水域为危险水域,有一渔船误入离灯塔A 2 km远的B处,为了尽快驶离危险区域,该船应按哪条射线方向航行?并说明理由.本节课学到了什么?与同伴交流.
点与圆的位置关系
利用圆的半径解决实际问题2课时流程逐点
导讲练课堂小结作业提升1.什么是圆?
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等,到圆心的距离等于半径
的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它
的另一个端点的运动轨迹就是一个圆.
2.点与圆的位置关系有哪些?如何判断?1知识点同圆的半径相等知1-讲如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两点,且AC=BD,求证:AD=BC. 例1知1-讲要证AD=BC,需证其所在的三角形全等,即需证
△ADO≌△BCO.导引:∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OC=OD.
在△ADO和△BCO中,
∴△ADO≌△BCO.
∴AD=BC.证明:知1-讲(1)本例中的OA=OB,即“圆的半径相等”,在以后的
证明中,可直接应用.
(2)“同圆的半径相等”在证明圆中线段相等时有着广泛
应用,应熟练掌握. ,知1-讲如图, AB为⊙O的直径, 点C, D在⊙O上, 已知∠BOC
=70°,AD∥OC,则∠AOD=________. 例2∵AD∥OC,
∴∠DAO=∠BOC=70°.
又∵OA=OD,
∴∠ADO=∠DAO=70°.
∴∠AOD=180°-∠ADO-∠DAO=40°.导引:40°知1-讲本题利用同圆中的半径相等求相关角的度数.如图,AB是⊙O的弦,半径OC,OD分别交AB于点
E,F,且AE=BF,请你判断线段OE与OF的数量
关系,并说明理由.知1-练如图,CD是⊙O的直径,点A在DC的延长线上,∠A
=20°,AE交⊙O于点B,且AB=OC.求:
(1)∠AOB的度数;
(2)∠EOD的度数.知1-练2知识点点与圆的位置关系知2-讲平面上有⊙O及一点P,点P到⊙O上一点的距离最大
为6 cm,最小为2 cm,则⊙O的半径为____________. 例3解答此题应进行分类讨论,点P可能位于圆的内部,
也可能位于圆的外部.当点P在圆内时,直径=6+2
=8(cm),因而半径是4 cm;当点P在圆外时,直径
=6-2=4(cm),因而半径是2 cm.所以⊙O的半径为
4 cm或2 cm.导引:4 cm或2 cm知2-讲 涉及点与圆的位置关系的最值问题,关键是要
运用分类讨论思想,其次是理解最大距离和最小距
离的意义.知2-讲如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.
(1)以点C为圆心,6为半径作圆,
试判断点A,D,B与 圆C的位置关系;
(2)当圆C的半径为多少时,点O在圆C上?
(3)若以点C为圆心作圆,使A,O,B三点至少有一点在圆内,至少有一点在圆外,则圆C的半径r的取值范围是什么?(直接写出答案) 例4知2-讲将点到圆心的距离d与半径r进行比较,当d<r时,点在圆内;
当d=r时,点在圆上;当d>r时,点在圆外.导引:(1)在Rt△ABC中,∠ACB=90°,AB=10,BC=8,
由勾股定理得AC=6=r,所以点A在圆C上.
由S△ACB= CD·AB= AC·BC,
得CD=4.8<6=r,所以点D在圆C内.
又因为BC=8>6=r,所以点B在圆C外.
(2)如图,连接CO,在Rt△ABC中,O为斜边AB的中点,所以
CO= AB= ×10=5,所以当圆C的半径为5时,点O
在圆C上.
(3)半径r的取值范围是5<r<8.解:知2-讲 判断点与圆的位置关系的实质就是将圆心和此点
连线的长度与半径进行比较,点与圆的位置关系的数
量特征是我们判断点与圆的位置关系的重要依据.如图,在△ABC中,∠ACB=90°,AB=10,BC
=8,CD⊥AB于D,O为AB的中点.
(1)以C为圆心,6为半径作圆,
试判断点A,D,B与⊙C的位置关系;
(2)当⊙C的半径为多少时,点O在⊙C上?
(3)若以点C为圆心作圆,使A,O,B三点至少有一点在圆内,至少有一点在圆外,则⊙C的半径r的取值范围是什么?知2-练知3-讲3知识点利用圆的半径解决实际问题 如图,有两条公路OM,ON相交成30°
角,沿公路OM方向离两条公路的交叉
处O点80 m的A处有一所学校,当拖拉
机沿ON方向行驶时,距拖拉机50 m范围内会受到噪音影响,已知有两台相距30 m的拖拉机正沿ON方向行驶,它们的速度均为5 m/s,则这两台拖拉机沿ON方向行驶时给学校带来噪音影响的时间是多少? 例5知3-讲如图,过点A作AC⊥ON,垂足为C.
∵∠MON=30°,OA=80 m,∴AC=40 m.
设第一台拖拉机到B点时开始对学校产生噪音影响,连接
AB,此时AB=50 m,由勾股定理得BC=30 m,
设第一台拖拉机到D点时噪音消失,连接AD,此时AD=50 m,
∴CD=30 m.解:知3-讲由于两台拖拉机相距30 m,
∴第一台到D点时第二台在C点,还需前行30 m后才对学校没
有噪音影响,
∴影响时间应是90÷5=18(s).
答:这两台拖拉机沿ON方向行驶时给学校带来噪音影响的时
间是18 s.知3-练如图,海军某部队在灯塔A周围进行爆破作业,灯塔A的周围3 km的水域为危险水域,有一渔船误入离灯塔A 2 km远的B处,为了尽快驶离危险区域,该船应按哪条射线方向航行?并说明理由.本节课学到了什么?与同伴交流.
