3.2 圆的对称性课件
图片预览








文档简介
课件28张PPT。第三章 圆第2节 圆的对称性1课堂讲解圆的中心对称性
圆心角、弧、弦之间的关系2课时流程逐点
导讲练课堂小结作业提升 一个圆绕着它的圆心旋转任意一个角度,还能
与原来的图形重合吗? 一个圆绕着它的圆心旋转任意一个角度,都能
与原来的图形重合.特别地,圆是中心对称图形,对
称中心为圆心.1知识点圆的中心对称性1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
要点精析:(1)圆是平面图形中唯一一个具有旋转不变性
的图形,也就是说旋转不变性是圆的特殊性质.
(2)圆既是轴对称图形,又是中心对称图形.知1-讲知1-讲 如图,在⊙O中,将△AOB绕圆心O顺时针旋转150°,
得到△COD,指出图中相等的量.例1导引:题中涉及的量有:弧、角、线段,
按圆的旋转不变性这一规律找相等的量.相等的弧有: ;
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,∠A
=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD. 解:知1-讲 将一个图形绕一个定点旋转时, 具有下列特性:一
是旋转角度、方向相同,二是图形的形状、大小保持
不变,因此本题圆中变换位置前后对应的弧、角、线
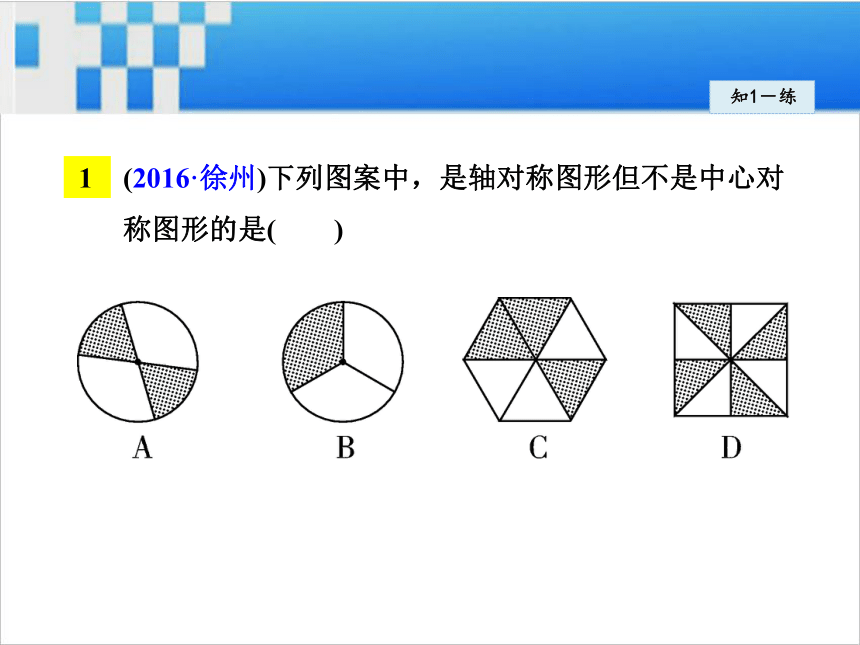
段都相等.知1-练(2016·徐州)下列图案中,是轴对称图形但不是中心对称图形的是( )知1-练(2016·凉山州)在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是( )
A.2个 B.3个 C.4个 D.5个知1-练下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴2知识点圆心角、弧、弦之间的关系知2-导 在等圆⊙O和⊙O ′中,分别作相等的圆心角∠AOB和
∠A ′O ′B ′ (如图),将两圆重叠,并固定圆心,然后把其
中的一个圆旋转一个角度,使 得OA与O ′A ′重合.
你能发现哪些等量关系?说一说你的理由.
知2-导小红认为 她是这样想的:
∵半径 OA与O ′A ′重合∠AOB=∠A ′O ′B ′ ,
∴半径OB与O ′B ′重合.
∵点A与点A ′重合,点B与点B ′重合,
∴ 与 重合,弦AB 与弦A'B'重合.
∴知2-导 在同圆或等圆中,如果两个圆心角所对的弧相等,那
么它们所对的弦相等 吗?这两个圆心角相等吗?你是怎
么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么
结论?知2-导1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.知2-讲1.弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
总结:在同圆或等圆中,如果两个圆心角、两条弧、两
条弦中有一组量相等,那么它们所对应的其余各组量都
分别相等.
知2-讲 要点精析:(1)上述三种关系成立的前提条件是“在同圆
或等圆中”,否则不成立.
(2)由于一条弦对着两条弧,“弦相等,所对的弧相等”中
的“弧相等”指的是“劣弧相等”或“优弧相等”.
拓展:(1)弦心距:圆心到圆的一条弦的距离叫做弦心距.
弦与弦心距的关系:在同一个圆中,两条弦相等,则它
们的弦心距相等,反之亦成立;在同一个圆中,弦越长,
则其弦心距越小.
(2)在同圆中,两条平行弦所夹的弧相等.知2-讲下列命题中,正确的是( )
①顶点在圆心的角是圆心角;
②相等的圆心角所对的弧也相等;
③在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.②和③
C.①和③ D.①②③例2C知2-讲导引:①根据圆心角的定义知,顶点在圆心的角是圆心角,
故正确;②缺少条件,必须是在同圆或等圆中,相等
的圆心角所对的弧才相等,故错误;③根据弧、弦、
圆心角之间的关系定理,可知在等圆中,若圆心角相
等,则所对的弦相等,若圆心角不等,则所对的弦也
不等,故正确.知2-讲本题考查了对弧、弦、圆心角之间的关系的理解,对于
圆中的一些易混易错结论应结合图形来解答.特别要注
意:看是否有“在同圆或等圆中”这个前提条件.知2-讲如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?例3解:BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.知2-讲〈菏泽〉如图,在Rt△ABC中,∠ACB=90°,∠A
=25°,以点C为圆心,BC为半径的圆交AB于点D,
交AC于点E,则 的度数为________.例4解:如图,连接CD,∵∠ACB=90°,
∠A=25°,∴∠B=65°.
∵CB=CD,∴∠B=∠CDB=65°.
∴∠BCD=50°.
∴ 的度数为50°.50°知2-讲在圆中,弧的度数就等于弧所对的圆心角的度数.知2-练下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等知2-练在⊙O中,圆心角∠AOB=2∠COD,则 与 的关系是( )
A. B.
C. D.不能确定知2-练(2016·舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
?
?
A.120° B.135° C.150° D.165°知2-练如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,若BC=CD=DA=4 cm,则⊙O的周长为( )
A.5π cm B.6π cm C.9π cm D.8π cm知2-练在⊙O中,M,N分别为弦AB,CD的中点,如果 OM=ON,那么在结论:①AB=CD;② ;③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
圆心角、弧、弦之间的关系2课时流程逐点
导讲练课堂小结作业提升 一个圆绕着它的圆心旋转任意一个角度,还能
与原来的图形重合吗? 一个圆绕着它的圆心旋转任意一个角度,都能
与原来的图形重合.特别地,圆是中心对称图形,对
称中心为圆心.1知识点圆的中心对称性1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
要点精析:(1)圆是平面图形中唯一一个具有旋转不变性
的图形,也就是说旋转不变性是圆的特殊性质.
(2)圆既是轴对称图形,又是中心对称图形.知1-讲知1-讲 如图,在⊙O中,将△AOB绕圆心O顺时针旋转150°,
得到△COD,指出图中相等的量.例1导引:题中涉及的量有:弧、角、线段,
按圆的旋转不变性这一规律找相等的量.相等的弧有: ;
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,∠A
=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD. 解:知1-讲 将一个图形绕一个定点旋转时, 具有下列特性:一
是旋转角度、方向相同,二是图形的形状、大小保持
不变,因此本题圆中变换位置前后对应的弧、角、线
段都相等.知1-练(2016·徐州)下列图案中,是轴对称图形但不是中心对称图形的是( )知1-练(2016·凉山州)在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是( )
A.2个 B.3个 C.4个 D.5个知1-练下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴2知识点圆心角、弧、弦之间的关系知2-导 在等圆⊙O和⊙O ′中,分别作相等的圆心角∠AOB和
∠A ′O ′B ′ (如图),将两圆重叠,并固定圆心,然后把其
中的一个圆旋转一个角度,使 得OA与O ′A ′重合.
你能发现哪些等量关系?说一说你的理由.
知2-导小红认为 她是这样想的:
∵半径 OA与O ′A ′重合∠AOB=∠A ′O ′B ′ ,
∴半径OB与O ′B ′重合.
∵点A与点A ′重合,点B与点B ′重合,
∴ 与 重合,弦AB 与弦A'B'重合.
∴知2-导 在同圆或等圆中,如果两个圆心角所对的弧相等,那
么它们所对的弦相等 吗?这两个圆心角相等吗?你是怎
么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么
结论?知2-导1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.知2-讲1.弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
总结:在同圆或等圆中,如果两个圆心角、两条弧、两
条弦中有一组量相等,那么它们所对应的其余各组量都
分别相等.
知2-讲 要点精析:(1)上述三种关系成立的前提条件是“在同圆
或等圆中”,否则不成立.
(2)由于一条弦对着两条弧,“弦相等,所对的弧相等”中
的“弧相等”指的是“劣弧相等”或“优弧相等”.
拓展:(1)弦心距:圆心到圆的一条弦的距离叫做弦心距.
弦与弦心距的关系:在同一个圆中,两条弦相等,则它
们的弦心距相等,反之亦成立;在同一个圆中,弦越长,
则其弦心距越小.
(2)在同圆中,两条平行弦所夹的弧相等.知2-讲下列命题中,正确的是( )
①顶点在圆心的角是圆心角;
②相等的圆心角所对的弧也相等;
③在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.②和③
C.①和③ D.①②③例2C知2-讲导引:①根据圆心角的定义知,顶点在圆心的角是圆心角,
故正确;②缺少条件,必须是在同圆或等圆中,相等
的圆心角所对的弧才相等,故错误;③根据弧、弦、
圆心角之间的关系定理,可知在等圆中,若圆心角相
等,则所对的弦相等,若圆心角不等,则所对的弦也
不等,故正确.知2-讲本题考查了对弧、弦、圆心角之间的关系的理解,对于
圆中的一些易混易错结论应结合图形来解答.特别要注
意:看是否有“在同圆或等圆中”这个前提条件.知2-讲如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?例3解:BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.知2-讲〈菏泽〉如图,在Rt△ABC中,∠ACB=90°,∠A
=25°,以点C为圆心,BC为半径的圆交AB于点D,
交AC于点E,则 的度数为________.例4解:如图,连接CD,∵∠ACB=90°,
∠A=25°,∴∠B=65°.
∵CB=CD,∴∠B=∠CDB=65°.
∴∠BCD=50°.
∴ 的度数为50°.50°知2-讲在圆中,弧的度数就等于弧所对的圆心角的度数.知2-练下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等知2-练在⊙O中,圆心角∠AOB=2∠COD,则 与 的关系是( )
A. B.
C. D.不能确定知2-练(2016·舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
?
?
A.120° B.135° C.150° D.165°知2-练如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,若BC=CD=DA=4 cm,则⊙O的周长为( )
A.5π cm B.6π cm C.9π cm D.8π cm知2-练在⊙O中,M,N分别为弦AB,CD的中点,如果 OM=ON,那么在结论:①AB=CD;② ;③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
