3.4.2 圆周角和直径的关系课件
图片预览








文档简介
课件21张PPT。第三章 圆3.4 圆周角和圆心角的关系第2课时 圆周角和直径
的关系1课堂讲解直径所对的圆周角是直角
直角所对的弦是直径2课时流程逐点
导讲练课堂小结作业提升复习回顾
1.什么叫做圆周角?
2.圆周角定理是什么?
3.圆周角定理的推论1的内容是什么?1知识点直径所对的圆周角是直角 在如图中,BC是⊙O的直径,它所对的圆周角有什么
特点?你能证 明你的结论吗?知1-讲问 题知1-导推论 直径所对的圆周角是直角1.圆周角定理的推论2(1):
推论 直径所对的圆周角是直角.
2. 要点精析:一般情况下,当条件中有直径时,往往
作出直径所对的圆周角,从而得到直角三角形,为
进一步解题创造条件.
知1-讲如图,AB是⊙O的直径,弦BC=BD,
若∠BOD=65°,求∠A的度数.知1-讲要求∠A的度数,可将其转化为求
所对的圆心角的度数,这样就需要连
接OC这条辅助线了.
导引: 例1如图,连接OC,∵BC=BD,
∴∠BOC=∠BOD=65°.
∴∠A= ∠BOC= ×65°=32.5°.解:知1-讲同圆或等圆中的弦、弧、圆心角、圆周角之间的关系
可以互相转化,当某个结论不好求时,可运用转化思
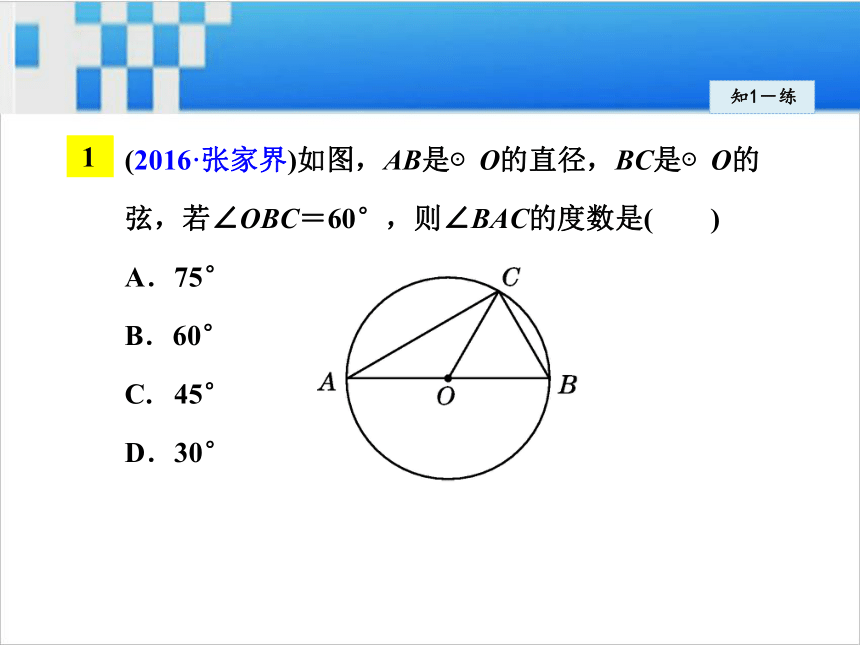
想将其转化为求与之相关的另一结论.(2016·张家界)如图,AB是⊙O的直径,BC是⊙O的
弦,若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C. 45°
D.30°知1-练(2016·娄底)如图,已知AB是⊙O的直径,∠D=40°,
则∠CAB的度数为( )
A.20°
B.40°
C.50°
D.70°知1-练如图,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.36°
B.46°
C.27°
D.63°知1-练(中考·连云港)如图,点P在以AB为直径的半圆内,连接AP,BP,并延长分别交半圆于点C,D,连接AD,BC并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.
A.①③
B.①④
C.②④
D.③④知1-练2知识点直角所对的弦是直径知2-导在如图中,圆周角∠A=90°,弦BC是直径吗?为什么?问 题知2-导90°的圆周角所对的弦是直径.知2-讲1.圆周角定理的推论2(2):
90°的圆周角所对的弦是直径.
要点精析:
当圆中有90°的圆周角时,连接90°角的两边与
圆的另一个交点,所成的弦是圆的直径.知2-讲(2015·兰州)如图,已知经过原点的⊙P
与x轴、y轴分别交于A,B两点,点C
是劣弧OB上一点,则∠ACB等于( )
A.80° B.90° C.100° D.无法确定例2由∠AOB与∠ACB 是优弧AB所对的圆周角,根据圆周
角定理,即可求得∠ACB =∠AOB= 90°.导引:∵∠AOB与∠ACB 是优弧AB所对的圆周角,
∴∠AOB =∠ACB,
∵ ∠AOB = 90°,∴ ∠ACB = 90°.解:B知2-讲 此题考查了圆周角定理,此题比较简单,解题的
关键是观察图形,得到∠AOB与∠ACB 是优弧AB所对
的圆周角.下列结论正确的是( )
A.直径所对的角是直角
B.90°的圆心角所对的弦是直径
C.同一条弦所对的圆周角相等
D.半圆所对的圆周角是直角 知2-练知2-练(中考·台州)从下列直角三角尺与圆弧的位置关系中,
可判断圆弧为半圆的是( )知2-练(中考·黔南州)如图,直径为10的⊙A经过点C(0,6)和
点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆
弧上一点,则cos∠OBC=________.1.已知直径时,常添加辅助线构造直角三角形,即“见直径想
直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,
遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中
作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行
两种转化:一是利用同弧所对的圆周角相等,进行角与角之
间的转化,二是将圆周角相等的问题转化为弦相等或弧相等
的问题.
的关系1课堂讲解直径所对的圆周角是直角
直角所对的弦是直径2课时流程逐点
导讲练课堂小结作业提升复习回顾
1.什么叫做圆周角?
2.圆周角定理是什么?
3.圆周角定理的推论1的内容是什么?1知识点直径所对的圆周角是直角 在如图中,BC是⊙O的直径,它所对的圆周角有什么
特点?你能证 明你的结论吗?知1-讲问 题知1-导推论 直径所对的圆周角是直角1.圆周角定理的推论2(1):
推论 直径所对的圆周角是直角.
2. 要点精析:一般情况下,当条件中有直径时,往往
作出直径所对的圆周角,从而得到直角三角形,为
进一步解题创造条件.
知1-讲如图,AB是⊙O的直径,弦BC=BD,
若∠BOD=65°,求∠A的度数.知1-讲要求∠A的度数,可将其转化为求
所对的圆心角的度数,这样就需要连
接OC这条辅助线了.
导引: 例1如图,连接OC,∵BC=BD,
∴∠BOC=∠BOD=65°.
∴∠A= ∠BOC= ×65°=32.5°.解:知1-讲同圆或等圆中的弦、弧、圆心角、圆周角之间的关系
可以互相转化,当某个结论不好求时,可运用转化思
想将其转化为求与之相关的另一结论.(2016·张家界)如图,AB是⊙O的直径,BC是⊙O的
弦,若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C. 45°
D.30°知1-练(2016·娄底)如图,已知AB是⊙O的直径,∠D=40°,
则∠CAB的度数为( )
A.20°
B.40°
C.50°
D.70°知1-练如图,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.36°
B.46°
C.27°
D.63°知1-练(中考·连云港)如图,点P在以AB为直径的半圆内,连接AP,BP,并延长分别交半圆于点C,D,连接AD,BC并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.
A.①③
B.①④
C.②④
D.③④知1-练2知识点直角所对的弦是直径知2-导在如图中,圆周角∠A=90°,弦BC是直径吗?为什么?问 题知2-导90°的圆周角所对的弦是直径.知2-讲1.圆周角定理的推论2(2):
90°的圆周角所对的弦是直径.
要点精析:
当圆中有90°的圆周角时,连接90°角的两边与
圆的另一个交点,所成的弦是圆的直径.知2-讲(2015·兰州)如图,已知经过原点的⊙P
与x轴、y轴分别交于A,B两点,点C
是劣弧OB上一点,则∠ACB等于( )
A.80° B.90° C.100° D.无法确定例2由∠AOB与∠ACB 是优弧AB所对的圆周角,根据圆周
角定理,即可求得∠ACB =∠AOB= 90°.导引:∵∠AOB与∠ACB 是优弧AB所对的圆周角,
∴∠AOB =∠ACB,
∵ ∠AOB = 90°,∴ ∠ACB = 90°.解:B知2-讲 此题考查了圆周角定理,此题比较简单,解题的
关键是观察图形,得到∠AOB与∠ACB 是优弧AB所对
的圆周角.下列结论正确的是( )
A.直径所对的角是直角
B.90°的圆心角所对的弦是直径
C.同一条弦所对的圆周角相等
D.半圆所对的圆周角是直角 知2-练知2-练(中考·台州)从下列直角三角尺与圆弧的位置关系中,
可判断圆弧为半圆的是( )知2-练(中考·黔南州)如图,直径为10的⊙A经过点C(0,6)和
点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆
弧上一点,则cos∠OBC=________.1.已知直径时,常添加辅助线构造直角三角形,即“见直径想
直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,
遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中
作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行
两种转化:一是利用同弧所对的圆周角相等,进行角与角之
间的转化,二是将圆周角相等的问题转化为弦相等或弧相等
的问题.
