3.5 确定圆的条件 课件
图片预览








文档简介
课件28张PPT。第三章 圆第5节 确定圆的条件1课堂讲解确定圆的条件
三角形的外接圆、外心2课时流程逐点
导讲练课堂小结作业提升 经过一点可以作无数条直线,经过两点可以确定
一条直线.那么,经过几 点能确定一个圆?1知识点确定圆的条件(1)作圆,使它经过已知点A.你能作出几个这样的圆?
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几
个这样的圆?其圆心的位置有什么特点?与线段AB有什么
关系?为什么?
(3)作圆,使它经过已知点木A,B,C(A,B,C三点不在同一
条直线上). 你是如何做的?你能作出几个这样的圆?知1-导做一做知1-导利用尺规过不在同一条直线上的三点作圆的方法如下:说说以上作法的道理.知1-导 在上面的作图过程中,因为直线DE和FG只有一个
交点O,并且点O到 A,B,C三个点的距离相等,所以经
过A,B,C三个点可以作一个圆,并且 只能作一个圆.知1-讲1. 经过一点可作无数个圆;过已知的两点可作无数个圆.
不在同一条直线上的三个点确定一个圆.
2. 确定一个圆的条件:
(1)已知圆心、半径可确定一个圆.
(2)不在同一条直线上的三个点确定一个圆.
拓展:
过多点作圆,先过不在同一直线上的三点作一个圆,
再看其他点是否在圆上.是则能作;不是,就不能作.
3. 易错警示:三点确定一个圆时,前提条件是“不在同
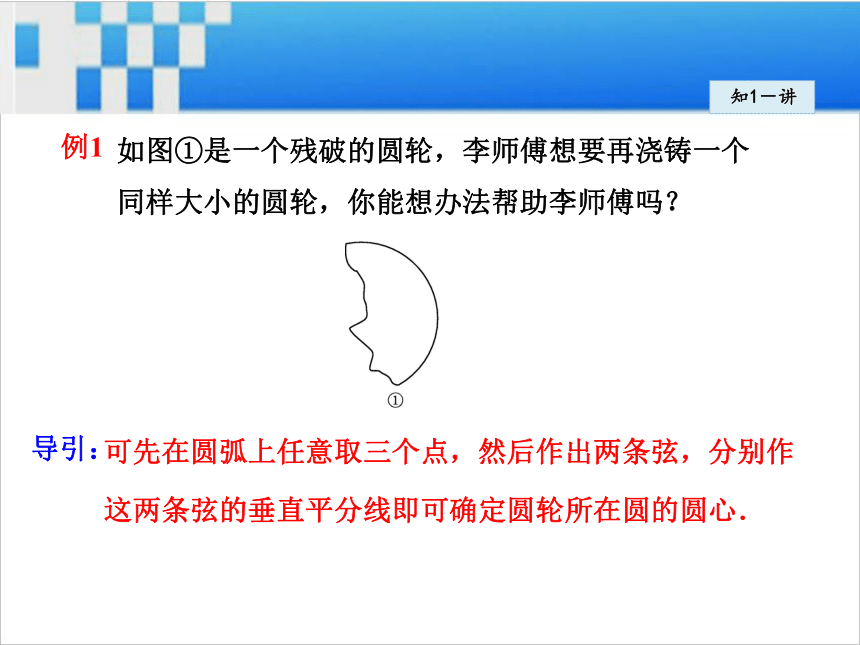
一直线上”的三点.知1-讲如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1导引:可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.知1-讲解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所
在的圆.知1-讲 经过不在同一条直线上的三点A,B,C作圆,
圆心O是线段AB,BC的垂直平分线的交点,再以
OA(或OB,OC)为半径作圆即可,这样的圆只能作
一个.知1-练下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆知1-练如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4知1-练已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个知1-练如图,在5×5的正方形网格中,一条圆弧经过A,
B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M2知识点三角形的外接圆、外心知2-讲1. 三角形的三个顶点确定一个圆,这个圆叫做三角形的外
接圆,外接圆的圆心是三角形三边垂直平分线的交点,
叫做三角形的外心.这个三角形叫做这个圆的内接三角
形.
要点精析:
(1)任何一个三角形都有一个外接圆,而一个圆有无数个
内接三角形.知2-讲(2)锐角三角形的外心在三角形的内部;直角三角形的外
心在斜边中点处;钝角三角形的外心在三角形的外部.
(3)三角形的外心到三角形三个顶点的距离相等.
2.三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距
离为半径作圆即可.知2-讲如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)例2D知2-讲导引:由A(1,4),B(5,4)可知AB∥x轴,△ABC的外接圆
圆心在线段AB的垂直平分线上,所以圆心的横坐标
应为 =3;同理,圆心还应在线段AC的垂直平
分线上,其纵坐标应为 =1.知2-讲 根据垂径定理的推论“弦的垂直平分线必过圆心”,
作两条弦的垂直平分线,交点即为圆心.知2-讲如图1,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O的半径.例3知2-讲导引:要求⊙O的半径,已知弦AB的长,需以AB为边与
⊙O的半径(或直径)构成等腰直角三角形,因此有
两个切入点.方法一:如图2,连接OA,OB,利
用圆周角定理可得∠AOB=2∠C=90°,再利用
勾股定理求出半径;方法二:
如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.知2-讲解:方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .知2-讲方法二:如图2,作直径AD,连接BD,设⊙O的半径
为r.
∵AD为⊙O的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,即42+42=(2r)2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .知2-讲 求三角形的外接圆半径时,最常用的办法是作出
圆心与三角形顶点的连线(即半径),延长使这条半径
变为直径,将求半径转化为直角三角形中求边的长.知2-练下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心不一定在三
角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4知2-练(2015·河北)如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的
是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE知2-练如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(2,1),点C的坐标为(2,-3),
则经画图操作可知△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)1.确定圆的条件:
不在同一条直线上的三个点确定一个圆.
2.三角形外心的性质:三角形的外心是它的外接圆的圆心,它是
三角形三边垂直平分线的交点,它到三角形各个顶点的距离相
等;锐角三角形的外心在三角形的内部,直角三角形的外心是
斜边的中点,钝角三角形的外心在三角形的外部.
3.三角形的外接圆有且只有一个;一个圆的内接三角形却有无
数个,这些三角形的外心重合.
三角形的外接圆、外心2课时流程逐点
导讲练课堂小结作业提升 经过一点可以作无数条直线,经过两点可以确定
一条直线.那么,经过几 点能确定一个圆?1知识点确定圆的条件(1)作圆,使它经过已知点A.你能作出几个这样的圆?
(2)作圆,使它经过已知点A,B.你是如何做的?你能作出几
个这样的圆?其圆心的位置有什么特点?与线段AB有什么
关系?为什么?
(3)作圆,使它经过已知点木A,B,C(A,B,C三点不在同一
条直线上). 你是如何做的?你能作出几个这样的圆?知1-导做一做知1-导利用尺规过不在同一条直线上的三点作圆的方法如下:说说以上作法的道理.知1-导 在上面的作图过程中,因为直线DE和FG只有一个
交点O,并且点O到 A,B,C三个点的距离相等,所以经
过A,B,C三个点可以作一个圆,并且 只能作一个圆.知1-讲1. 经过一点可作无数个圆;过已知的两点可作无数个圆.
不在同一条直线上的三个点确定一个圆.
2. 确定一个圆的条件:
(1)已知圆心、半径可确定一个圆.
(2)不在同一条直线上的三个点确定一个圆.
拓展:
过多点作圆,先过不在同一直线上的三点作一个圆,
再看其他点是否在圆上.是则能作;不是,就不能作.
3. 易错警示:三点确定一个圆时,前提条件是“不在同
一直线上”的三点.知1-讲如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1导引:可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.知1-讲解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所
在的圆.知1-讲 经过不在同一条直线上的三点A,B,C作圆,
圆心O是线段AB,BC的垂直平分线的交点,再以
OA(或OB,OC)为半径作圆即可,这样的圆只能作
一个.知1-练下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆知1-练如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4知1-练已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个知1-练如图,在5×5的正方形网格中,一条圆弧经过A,
B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M2知识点三角形的外接圆、外心知2-讲1. 三角形的三个顶点确定一个圆,这个圆叫做三角形的外
接圆,外接圆的圆心是三角形三边垂直平分线的交点,
叫做三角形的外心.这个三角形叫做这个圆的内接三角
形.
要点精析:
(1)任何一个三角形都有一个外接圆,而一个圆有无数个
内接三角形.知2-讲(2)锐角三角形的外心在三角形的内部;直角三角形的外
心在斜边中点处;钝角三角形的外心在三角形的外部.
(3)三角形的外心到三角形三个顶点的距离相等.
2.三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距
离为半径作圆即可.知2-讲如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)例2D知2-讲导引:由A(1,4),B(5,4)可知AB∥x轴,△ABC的外接圆
圆心在线段AB的垂直平分线上,所以圆心的横坐标
应为 =3;同理,圆心还应在线段AC的垂直平
分线上,其纵坐标应为 =1.知2-讲 根据垂径定理的推论“弦的垂直平分线必过圆心”,
作两条弦的垂直平分线,交点即为圆心.知2-讲如图1,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O的半径.例3知2-讲导引:要求⊙O的半径,已知弦AB的长,需以AB为边与
⊙O的半径(或直径)构成等腰直角三角形,因此有
两个切入点.方法一:如图2,连接OA,OB,利
用圆周角定理可得∠AOB=2∠C=90°,再利用
勾股定理求出半径;方法二:
如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.知2-讲解:方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .知2-讲方法二:如图2,作直径AD,连接BD,设⊙O的半径
为r.
∵AD为⊙O的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,即42+42=(2r)2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .知2-讲 求三角形的外接圆半径时,最常用的办法是作出
圆心与三角形顶点的连线(即半径),延长使这条半径
变为直径,将求半径转化为直角三角形中求边的长.知2-练下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心不一定在三
角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4知2-练(2015·河北)如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的
是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE知2-练如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(2,1),点C的坐标为(2,-3),
则经画图操作可知△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)1.确定圆的条件:
不在同一条直线上的三个点确定一个圆.
2.三角形外心的性质:三角形的外心是它的外接圆的圆心,它是
三角形三边垂直平分线的交点,它到三角形各个顶点的距离相
等;锐角三角形的外心在三角形的内部,直角三角形的外心是
斜边的中点,钝角三角形的外心在三角形的外部.
3.三角形的外接圆有且只有一个;一个圆的内接三角形却有无
数个,这些三角形的外心重合.
