3.7 切线长定理 课件
图片预览







文档简介
课件25张PPT。第三章 圆第7节 切线长定理1课堂讲解切线长定理2课时流程逐点
导讲练课堂小结作业提升过圆外一点画圆的切线,你能画出几条?试试看.知识点切线长定理如图,PA,PB是⊙O的两条切线,A ,
B是切点
(1)这个图形是轴对称图形吗?如果是,
它的对称轴是什么?
(2)在这个图中你能找到相等的线段吗?说说你的理由.知1-导1知1-导 过圆外一点画圆的切线,这点和切点之间的线段
长叫做这点到圆的切线长.知1-讲1. 切线长定义:经过圆外的一点画圆的切线,这点和切点
之间的线段的长,叫做这点到圆的切线长.
要点精析:切线是直线,不可度量;切线长是切线上切点
与切点外另一点之间的线段的长,可以度量.
2.切线长定理:过圆外一点所画的圆的两条切线长相等.
要点精析:这一点和圆心的连线平分两条切线的夹角,
(1)由切线长定理既可以得到线段相等,又可以得到角相
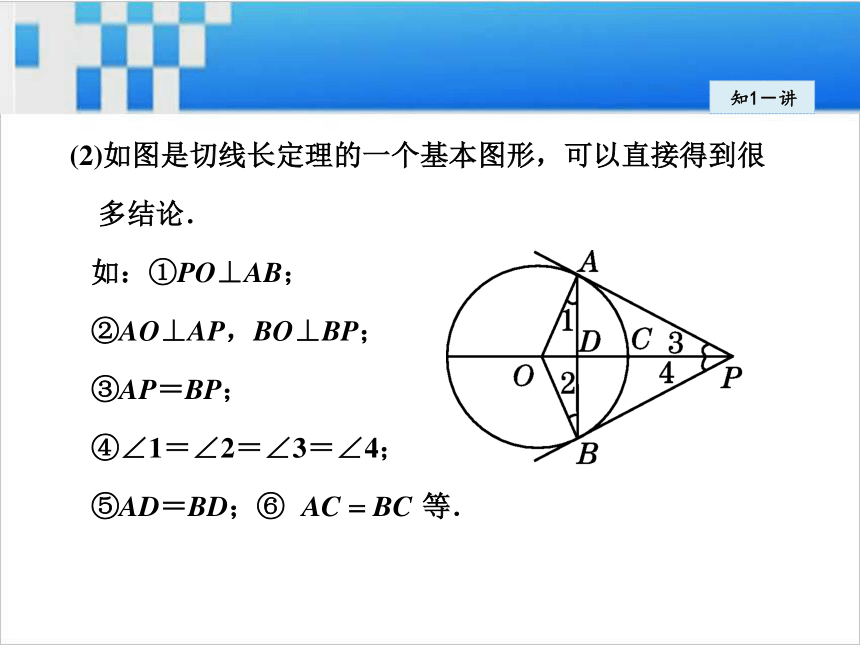
等,运用时要根据题意选用.知1-讲(2)如图是切线长定理的一个基本图形,可以直接得到很
多结论.
如:①PO⊥AB;
②AO⊥AP,BO⊥BP;
③AP=BP;
④∠1=∠2=∠3=∠4;
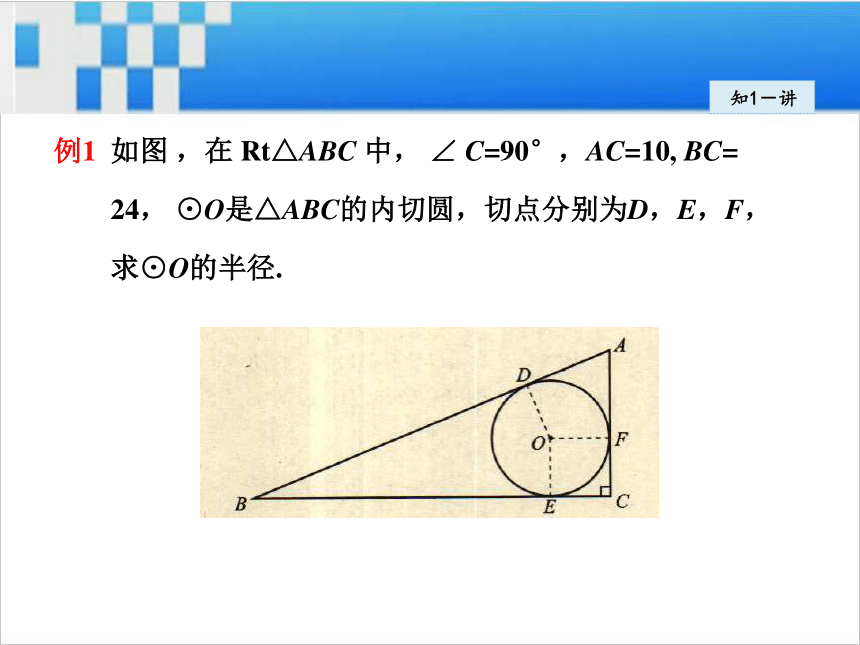
⑤AD=BD;⑥ 等.知1-讲如图 ,在 Rt△ABC 中, ∠ C=90°,AC=10, BC=
24, ⊙O是△ABC的内切圆,切点分别为D,E,F,
求⊙O的半径.例1知1-讲解:连接OD,OE,OF,则OD=OE=OF,设OD=r.
在 △ABC中,AC=10, BC=24,
∴AB = = 26.
∵ ⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,
AD = AF,CE=CF.知1-讲又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26,
∴ 34 -2r = 26.
∴ r = 4,
即 ⊙O 的半径为4.知1-讲如图,直尺、三角尺均和圆O相切,AB=8 cm,
求圆O的直径.例2知1-讲导引:连接OE,OA,OB,根据切线长定理和切线性质可
得∠OBA=90°,∠OAE=∠OAB= ∠BAC,求
∠BAC即可求出∠OAB和∠BOA,进而求出OA,
再根据勾股定理求出OB即可.解:如图,连接OE,OA,OB.
∵AC,AB都是⊙O的切线,切点分别是E,B,
∴∠OBA=90°,∠OAE=∠OAB= ∠BAC.
∵∠CAD=60°,∴∠BAC=120°,
∴∠OAB= ×120°=60°,
∴∠BOA=30°,∴OA=2AB=16 cm,
由勾股定理得OB= (cm),
即⊙O的半径是 cm,∴⊙O的直径是 cm.,知1-讲知1-讲 如图,PA,PB是⊙O的切线,A,B是切点,点C是 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为________,∠DOE的度数为________.例360°6知1-讲导引:如图,连接PO,CO,AO,BO,DO,EO,由切线长
定理知PA=PB,DC=DA,EC=EB,因而△PDE的
周长可转化为PA+PB,即2PA.又由切线长定理易得
∠DOC= ∠AOC,∠EOC= ∠BOC,∴∠DOE=
(∠AOC+∠BOC)= ∠AOB.由∠APB=60°得
∠APO=30°.又∵AO= ,
由切线的性质得∠PAO=90°,∠PBO=90°,
∴PO= ,∠AOB=180°-∠APB=120°.
∴PA= =3,∠DOE= ∠AOB=60°.知1-讲利用切线长定理进行几何计算时,要注意构成切线长定
理的基本图形,作过切点的半径、连接圆外一点与圆心
是常用的作辅助线的方法.由于切线长定理涉及的线段、
角较多,因此熟记基本图形的相关结论是解题的关键,
而三角形的有关性质在解决有关切线问题时,也起到了
很好的辅助作用.知1-讲〈天津〉已知⊙O中,AC为直径,MA,MB分别切
⊙O于点A,B.
(1)如图①,若∠BAC=25°,求∠AMB的大小;
(2)如图②,过点B作BD⊥AC于点E,交⊙O于点D,
若BD=MA,求∠AMB的大小.例4知1-讲导引:(1)要求∠AMB的大小,由切线长定理知△MAB为等腰
三角形,只需求出∠MAB,即可得解.(2)要求∠AMB
的大小,因为题中无已知角的度数,因此需要证明
∠AMB为特殊直角三角形中的角,所以先作出直角三
角形,再寻求求角的条件.知1-讲解:(1)如图①,连接OB,
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∠OBM=∠OAM=90°,
又∵∠OAB=25°,
∴∠MAB=90°-∠OAB=90°-25°=65°.
∴∠AMB=180°-2∠MAB=180°-2×65°=50°. 知1-讲解:(2)如图②,过点B作BH⊥AM于点H,
∵直径AC⊥BD,MA是⊙O的切线,
∴BE= BD,四边形BHAE是矩形,
∴HA=BE= BD.
又∵BD=MA,MA=MB,
∴MH= MB.在Rt△MBH中,
∵MH= MB,∴∠MBH=30°,
∴∠AMB=60°.知1-讲本题用到转化思想,综合运用垂径定理、切线的性质、
切线长定理,通过作垂线构造矩形和直角三角形,求出
角的度数.切线长定理在本题中起到了一个线段等量转
移的作用.知1-练1 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆
的半径知1-练如图,PA,PB是⊙O的切线,且∠APB=40°,
下列结论不正确的是( )
A.PA=PB
B.∠APO=20°
C.∠OBP=70°
D.∠AOP=70°知1-练(2015·南充)如图,PA和PB是⊙O的切线,点A和B
是切点,AC是⊙O的直径,已知∠P=40°,则
∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°切线长定理中的基本图形
如图,PA,PB为⊙O的切线,A,B分别为切点,则有:
(1)两个等腰三角形(△PAB,△OAB).
(2)一条特殊的角平分线(OP平分∠APB和∠AOB).
(3)三个垂直关系(OA⊥PA,OB⊥PB,OP⊥AB).
导讲练课堂小结作业提升过圆外一点画圆的切线,你能画出几条?试试看.知识点切线长定理如图,PA,PB是⊙O的两条切线,A ,
B是切点
(1)这个图形是轴对称图形吗?如果是,
它的对称轴是什么?
(2)在这个图中你能找到相等的线段吗?说说你的理由.知1-导1知1-导 过圆外一点画圆的切线,这点和切点之间的线段
长叫做这点到圆的切线长.知1-讲1. 切线长定义:经过圆外的一点画圆的切线,这点和切点
之间的线段的长,叫做这点到圆的切线长.
要点精析:切线是直线,不可度量;切线长是切线上切点
与切点外另一点之间的线段的长,可以度量.
2.切线长定理:过圆外一点所画的圆的两条切线长相等.
要点精析:这一点和圆心的连线平分两条切线的夹角,
(1)由切线长定理既可以得到线段相等,又可以得到角相
等,运用时要根据题意选用.知1-讲(2)如图是切线长定理的一个基本图形,可以直接得到很
多结论.
如:①PO⊥AB;
②AO⊥AP,BO⊥BP;
③AP=BP;
④∠1=∠2=∠3=∠4;
⑤AD=BD;⑥ 等.知1-讲如图 ,在 Rt△ABC 中, ∠ C=90°,AC=10, BC=
24, ⊙O是△ABC的内切圆,切点分别为D,E,F,
求⊙O的半径.例1知1-讲解:连接OD,OE,OF,则OD=OE=OF,设OD=r.
在 △ABC中,AC=10, BC=24,
∴AB = = 26.
∵ ⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,
AD = AF,CE=CF.知1-讲又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26,
∴ 34 -2r = 26.
∴ r = 4,
即 ⊙O 的半径为4.知1-讲如图,直尺、三角尺均和圆O相切,AB=8 cm,
求圆O的直径.例2知1-讲导引:连接OE,OA,OB,根据切线长定理和切线性质可
得∠OBA=90°,∠OAE=∠OAB= ∠BAC,求
∠BAC即可求出∠OAB和∠BOA,进而求出OA,
再根据勾股定理求出OB即可.解:如图,连接OE,OA,OB.
∵AC,AB都是⊙O的切线,切点分别是E,B,
∴∠OBA=90°,∠OAE=∠OAB= ∠BAC.
∵∠CAD=60°,∴∠BAC=120°,
∴∠OAB= ×120°=60°,
∴∠BOA=30°,∴OA=2AB=16 cm,
由勾股定理得OB= (cm),
即⊙O的半径是 cm,∴⊙O的直径是 cm.,知1-讲知1-讲 如图,PA,PB是⊙O的切线,A,B是切点,点C是 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为________,∠DOE的度数为________.例360°6知1-讲导引:如图,连接PO,CO,AO,BO,DO,EO,由切线长
定理知PA=PB,DC=DA,EC=EB,因而△PDE的
周长可转化为PA+PB,即2PA.又由切线长定理易得
∠DOC= ∠AOC,∠EOC= ∠BOC,∴∠DOE=
(∠AOC+∠BOC)= ∠AOB.由∠APB=60°得
∠APO=30°.又∵AO= ,
由切线的性质得∠PAO=90°,∠PBO=90°,
∴PO= ,∠AOB=180°-∠APB=120°.
∴PA= =3,∠DOE= ∠AOB=60°.知1-讲利用切线长定理进行几何计算时,要注意构成切线长定
理的基本图形,作过切点的半径、连接圆外一点与圆心
是常用的作辅助线的方法.由于切线长定理涉及的线段、
角较多,因此熟记基本图形的相关结论是解题的关键,
而三角形的有关性质在解决有关切线问题时,也起到了
很好的辅助作用.知1-讲〈天津〉已知⊙O中,AC为直径,MA,MB分别切
⊙O于点A,B.
(1)如图①,若∠BAC=25°,求∠AMB的大小;
(2)如图②,过点B作BD⊥AC于点E,交⊙O于点D,
若BD=MA,求∠AMB的大小.例4知1-讲导引:(1)要求∠AMB的大小,由切线长定理知△MAB为等腰
三角形,只需求出∠MAB,即可得解.(2)要求∠AMB
的大小,因为题中无已知角的度数,因此需要证明
∠AMB为特殊直角三角形中的角,所以先作出直角三
角形,再寻求求角的条件.知1-讲解:(1)如图①,连接OB,
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∠OBM=∠OAM=90°,
又∵∠OAB=25°,
∴∠MAB=90°-∠OAB=90°-25°=65°.
∴∠AMB=180°-2∠MAB=180°-2×65°=50°. 知1-讲解:(2)如图②,过点B作BH⊥AM于点H,
∵直径AC⊥BD,MA是⊙O的切线,
∴BE= BD,四边形BHAE是矩形,
∴HA=BE= BD.
又∵BD=MA,MA=MB,
∴MH= MB.在Rt△MBH中,
∵MH= MB,∴∠MBH=30°,
∴∠AMB=60°.知1-讲本题用到转化思想,综合运用垂径定理、切线的性质、
切线长定理,通过作垂线构造矩形和直角三角形,求出
角的度数.切线长定理在本题中起到了一个线段等量转
移的作用.知1-练1 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆
的半径知1-练如图,PA,PB是⊙O的切线,且∠APB=40°,
下列结论不正确的是( )
A.PA=PB
B.∠APO=20°
C.∠OBP=70°
D.∠AOP=70°知1-练(2015·南充)如图,PA和PB是⊙O的切线,点A和B
是切点,AC是⊙O的直径,已知∠P=40°,则
∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°切线长定理中的基本图形
如图,PA,PB为⊙O的切线,A,B分别为切点,则有:
(1)两个等腰三角形(△PAB,△OAB).
(2)一条特殊的角平分线(OP平分∠APB和∠AOB).
(3)三个垂直关系(OA⊥PA,OB⊥PB,OP⊥AB).
