3.8 圆内接正多边形 课件
图片预览










文档简介
课件32张PPT。第三章 圆第8节 圆内接正多边形1课堂讲解圆内接正多边形及相关定义
圆内接正多边形的画法2课时流程逐点
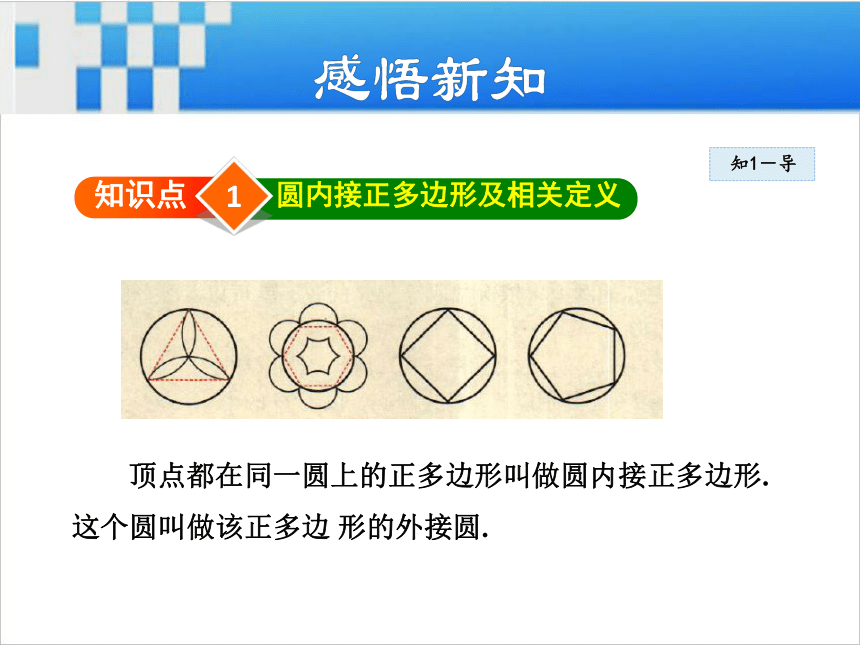
导讲练课堂小结作业提升请观察下列图形:1知识点圆内接正多边形及相关定义 顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边 形的外接圆.知1-导知1-导 把一个圆n等分(n≥3 ),依次连接各分点,我们 就可
以作出一个圆内接正多边形.
如图,五边形ABCDE是⊙O的内接
正五边 形,圆心O叫做这个正五边形
的中心;OA是这个正五边 形的半径;
∠ AOB是这个正五边形的中心角;OM丄BC,垂足
为M,OM是这个正五边形圆心距.知1-讲1.圆内接正多边形:顶点都在同一圆上的正多边形叫做圆
内接正多边形,这个圆叫做正多边形的外接圆.
2.与正多边形有关的概念:
(1)正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形的外接圆的半径叫做这个正多边形的半径.
(3)正多边形每一边所对的圆心角叫做这个正多边形的中心角.
(4)正多边形的中心到正多边形一边的距离叫做这个正多边形的
边心距.知1-讲 要点精析:
边心距与弦心距的关系:
边心距是圆心到正多边形一边的距离,此时的边心
距也可以看作正多边形的外接圆中,圆心到多边形的边
(即外接圆的弦)的距离,即边心距也是弦心距;但弦心
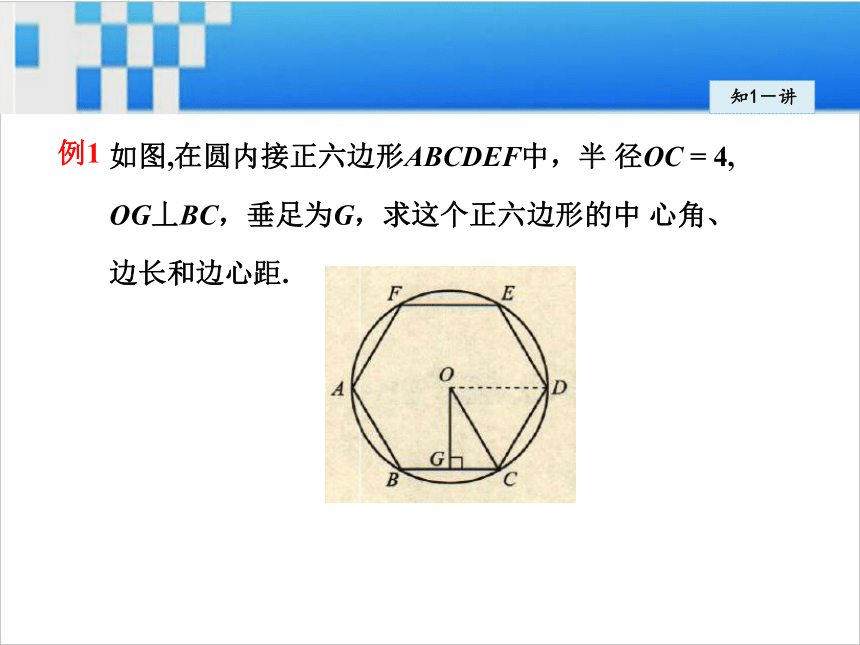
距不一定是边心距.知1-讲拓展:正多边形的有关计算:知1-讲如图,在圆内接正六边形ABCDEF中,半 径OC = 4,
OG丄BC,垂足为G,求这个正六边形的中 心角、
边长和边心距.例1知1-讲解:连接OD.∵六边形ABCDEF为正六边形,
∴ ∠ COD = = 60°
∴ △COD为等边三角形.
∴ CD = OC = 4.
在 Rt △ COG中,OC = 4,CG= BC= ×4=2,
∴ OG =
∴正六边形的中心角为60°,边长为4,边心距为知1-讲如图,五边形ABCDE内接于⊙O,∠A=∠B=∠C
=∠D=∠E.
求证:五边形ABCDE是正五边形.例2导引:根据同圆中相等的圆周角所对的弧相等,得出
利用等式的性质,两边同时减去 ,即可得到
,根据等弧所对的弦相等,得出BC=AE.知1-讲解:∵∠A=∠B=∠C=∠D=∠E,圆周角∠A对 ,
圆周角∠B对 ,
∴ .
∴ ,即 .
∴BC=AE.同理可证其余各边都相等.
∴五边形ABCDE是正五边形.知1-讲(1)证正多边形和圆的关系,在图形中找到圆的弧、弦
等,利用同(等)弧所对的圆周角相等、所对的弦相等解
答.其证明思路如下:角相等?弧相等?弦相等?
?正多边形.(2)证明一个多边形是正多边形的方法:①
利用定义,证出各边相等,各角相等;②利用圆内接多
边形,证明各边所对的弧相等,即把圆n等分,依次连
接各等分点,所得多边形即为正多边形.知1-练给出下列五个命题:
①各多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形;
⑤正n边形的中心角αn= ,且与每一个外角相等.
其中正确命题有( )
A.2个 B.3个 C.4个 D.5个知1-练(2016·南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2 C.2∶3 D.2∶π
知1-练(2015·青岛)如图,正六边形ABCDEF内接于⊙O,
若直线PA与⊙O相切于点A,则∠PAB等于( )
A.30° B.35° C.45° D.60°知1-练(2016·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.知1-练(2015·随州)如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°2知识点圆内接正多边形的画法知2-导利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.知2-导为了减少累积误差,通常像如图那样,作⊙O的 任意一条直
径FC,分别以F,C为圆心,以⊙O的半 径R为半径作弧,与
⊙O相交于点E,A和D,B则A, B,C,D,E,F是⊙O的六等
分点,顺次连接AB,BC,CD,DE,EF,FA,便得到正六
边形ABCDEF.知2-讲1. 用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可
以等分圆周,从而得到正多边形.采用“先用量角器画一个
的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”,这
种方法简便,误差小,且可以画任意正多边形.
2. 用尺规等分圆:用尺规作图的方法等分圆周,然后依次连接圆
上各分点得到正多边形,这种方法有局限性,不是任意正多边形
都能用此法作图.从理论上讲这是一种准确方法,但在作图时较
复杂,同样存在作图的误差.
3. 易错警示:作图时由于忽视累积误差的影响,导致作图不准,
应减少累积误差.知2-讲作一个正三角形,使其半径为0.9 cm.例3导引:先作出一个半径为0.9 cm的圆,再用量角器画出中心角
为120°的角(2个),依次连接与圆的交点即可;或将圆
六等分,再依次连接相隔一个的等分点即可.知2-讲解:作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.知2-讲作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.知2-讲解决这类问题通常有两种方法:
(1)用量角器等分圆周法;
(2)用尺规等分圆周法.知2-讲 如图①②③…,M,N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE……的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是________,
图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形边数n(n≥3)的关系式(直接
写出答案).例4知2-讲导引:如图①,连接OB,OC,因为BM=CN,OB=OC,且
易知∠OBM=∠OCN,所以△BOM≌△CON,所以
∠BOM=∠CON,进而易得∠MON=∠BOC,即转化
为求正三角形的中心角.类似地,其他图形中求
∠MON也可转化为求正多边形的中心角.知2-讲解:(1)如图①,连接OB,OC.
易知∠BOC= =120°,∠OBM=∠OCN=30°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN.∴∠BOM=∠CON.
∴∠BON+∠BOM=∠BON+∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72° (3)∠MON= (n≥3).知2-讲此题运用了从特殊到一般的思想.解决此类问题,关键
是对未知角先进行分析,再通过三角形全等进行角度的
等量转化.知2-练如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两
点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对知2-练在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).1.常见正多边形的边长与半径的关系:正六边形的边长等
于其外接圆半径,正三角形的边长等于其外接圆半径的
倍,正方形的边长等于其外接圆半径的 倍.
2.求解与正多边形有关的计算问题,关键是找出被半径和
边心距分割成的直角三角形,将正多边形的计算问题转
化为直角三角形问题.
圆内接正多边形的画法2课时流程逐点
导讲练课堂小结作业提升请观察下列图形:1知识点圆内接正多边形及相关定义 顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边 形的外接圆.知1-导知1-导 把一个圆n等分(n≥3 ),依次连接各分点,我们 就可
以作出一个圆内接正多边形.
如图,五边形ABCDE是⊙O的内接
正五边 形,圆心O叫做这个正五边形
的中心;OA是这个正五边 形的半径;
∠ AOB是这个正五边形的中心角;OM丄BC,垂足
为M,OM是这个正五边形圆心距.知1-讲1.圆内接正多边形:顶点都在同一圆上的正多边形叫做圆
内接正多边形,这个圆叫做正多边形的外接圆.
2.与正多边形有关的概念:
(1)正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形的外接圆的半径叫做这个正多边形的半径.
(3)正多边形每一边所对的圆心角叫做这个正多边形的中心角.
(4)正多边形的中心到正多边形一边的距离叫做这个正多边形的
边心距.知1-讲 要点精析:
边心距与弦心距的关系:
边心距是圆心到正多边形一边的距离,此时的边心
距也可以看作正多边形的外接圆中,圆心到多边形的边
(即外接圆的弦)的距离,即边心距也是弦心距;但弦心
距不一定是边心距.知1-讲拓展:正多边形的有关计算:知1-讲如图,在圆内接正六边形ABCDEF中,半 径OC = 4,
OG丄BC,垂足为G,求这个正六边形的中 心角、
边长和边心距.例1知1-讲解:连接OD.∵六边形ABCDEF为正六边形,
∴ ∠ COD = = 60°
∴ △COD为等边三角形.
∴ CD = OC = 4.
在 Rt △ COG中,OC = 4,CG= BC= ×4=2,
∴ OG =
∴正六边形的中心角为60°,边长为4,边心距为知1-讲如图,五边形ABCDE内接于⊙O,∠A=∠B=∠C
=∠D=∠E.
求证:五边形ABCDE是正五边形.例2导引:根据同圆中相等的圆周角所对的弧相等,得出
利用等式的性质,两边同时减去 ,即可得到
,根据等弧所对的弦相等,得出BC=AE.知1-讲解:∵∠A=∠B=∠C=∠D=∠E,圆周角∠A对 ,
圆周角∠B对 ,
∴ .
∴ ,即 .
∴BC=AE.同理可证其余各边都相等.
∴五边形ABCDE是正五边形.知1-讲(1)证正多边形和圆的关系,在图形中找到圆的弧、弦
等,利用同(等)弧所对的圆周角相等、所对的弦相等解
答.其证明思路如下:角相等?弧相等?弦相等?
?正多边形.(2)证明一个多边形是正多边形的方法:①
利用定义,证出各边相等,各角相等;②利用圆内接多
边形,证明各边所对的弧相等,即把圆n等分,依次连
接各等分点,所得多边形即为正多边形.知1-练给出下列五个命题:
①各多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形;
⑤正n边形的中心角αn= ,且与每一个外角相等.
其中正确命题有( )
A.2个 B.3个 C.4个 D.5个知1-练(2016·南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2 C.2∶3 D.2∶π
知1-练(2015·青岛)如图,正六边形ABCDEF内接于⊙O,
若直线PA与⊙O相切于点A,则∠PAB等于( )
A.30° B.35° C.45° D.60°知1-练(2016·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.知1-练(2015·随州)如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°2知识点圆内接正多边形的画法知2-导利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.知2-导为了减少累积误差,通常像如图那样,作⊙O的 任意一条直
径FC,分别以F,C为圆心,以⊙O的半 径R为半径作弧,与
⊙O相交于点E,A和D,B则A, B,C,D,E,F是⊙O的六等
分点,顺次连接AB,BC,CD,DE,EF,FA,便得到正六
边形ABCDEF.知2-讲1. 用量角器等分圆:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可
以等分圆周,从而得到正多边形.采用“先用量角器画一个
的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”,这
种方法简便,误差小,且可以画任意正多边形.
2. 用尺规等分圆:用尺规作图的方法等分圆周,然后依次连接圆
上各分点得到正多边形,这种方法有局限性,不是任意正多边形
都能用此法作图.从理论上讲这是一种准确方法,但在作图时较
复杂,同样存在作图的误差.
3. 易错警示:作图时由于忽视累积误差的影响,导致作图不准,
应减少累积误差.知2-讲作一个正三角形,使其半径为0.9 cm.例3导引:先作出一个半径为0.9 cm的圆,再用量角器画出中心角
为120°的角(2个),依次连接与圆的交点即可;或将圆
六等分,再依次连接相隔一个的等分点即可.知2-讲解:作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.知2-讲作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.知2-讲解决这类问题通常有两种方法:
(1)用量角器等分圆周法;
(2)用尺规等分圆周法.知2-讲 如图①②③…,M,N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE……的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是________,
图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形边数n(n≥3)的关系式(直接
写出答案).例4知2-讲导引:如图①,连接OB,OC,因为BM=CN,OB=OC,且
易知∠OBM=∠OCN,所以△BOM≌△CON,所以
∠BOM=∠CON,进而易得∠MON=∠BOC,即转化
为求正三角形的中心角.类似地,其他图形中求
∠MON也可转化为求正多边形的中心角.知2-讲解:(1)如图①,连接OB,OC.
易知∠BOC= =120°,∠OBM=∠OCN=30°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN.∴∠BOM=∠CON.
∴∠BON+∠BOM=∠BON+∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72° (3)∠MON= (n≥3).知2-讲此题运用了从特殊到一般的思想.解决此类问题,关键
是对未知角先进行分析,再通过三角形全等进行角度的
等量转化.知2-练如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两
点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对知2-练在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).1.常见正多边形的边长与半径的关系:正六边形的边长等
于其外接圆半径,正三角形的边长等于其外接圆半径的
倍,正方形的边长等于其外接圆半径的 倍.
2.求解与正多边形有关的计算问题,关键是找出被半径和
边心距分割成的直角三角形,将正多边形的计算问题转
化为直角三角形问题.
