1.1.2 正弦与余弦课件
图片预览





文档简介
课件28张PPT。第一章 直角三角形的边角关系1.1 锐角三角函数第2课时 正弦和余弦1课堂讲解正弦 余弦
锐角三角函数的取值范围 2课时流程逐点
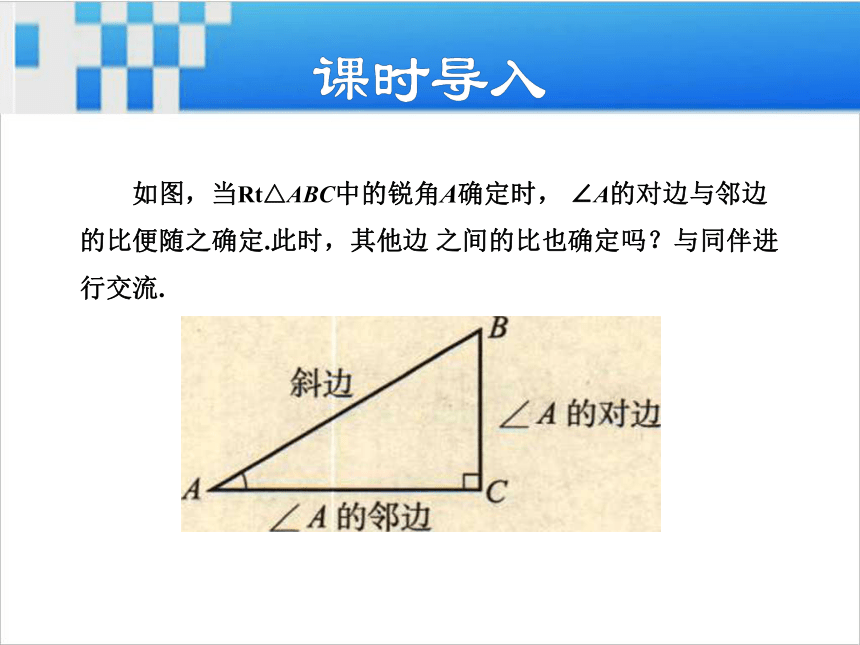
导讲练课堂小结作业提升 如图,当Rt△ABC中的锐角A确定时, ∠A的对边与邻边
的比便随之确定.此时,其他边 之间的比也确定吗?与同伴进
行交流.在Rt△ABC中,如果锐角A确定, 那么∠A的对边
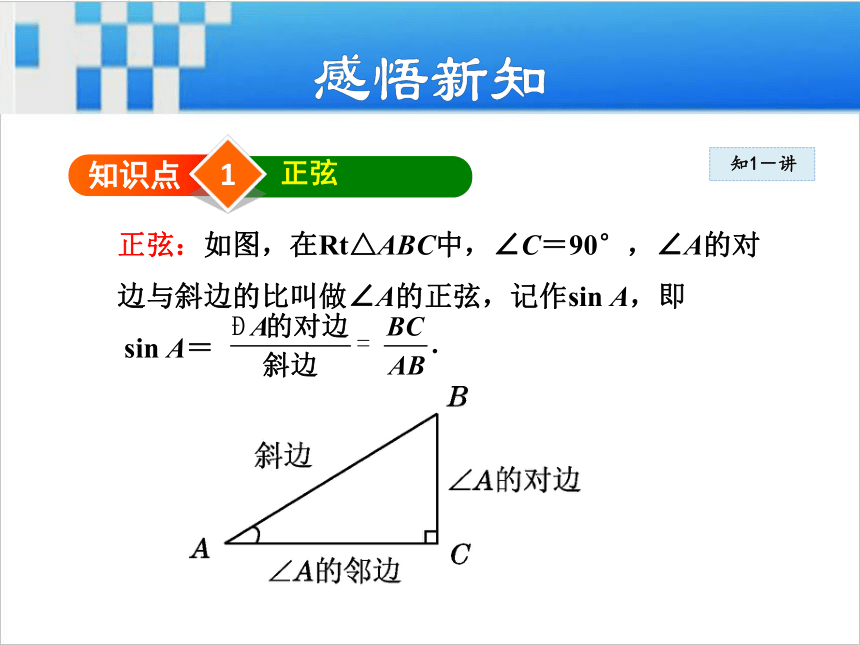
与斜边的比、邻边与斜边的比也随之确定. 1知识点正弦 正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
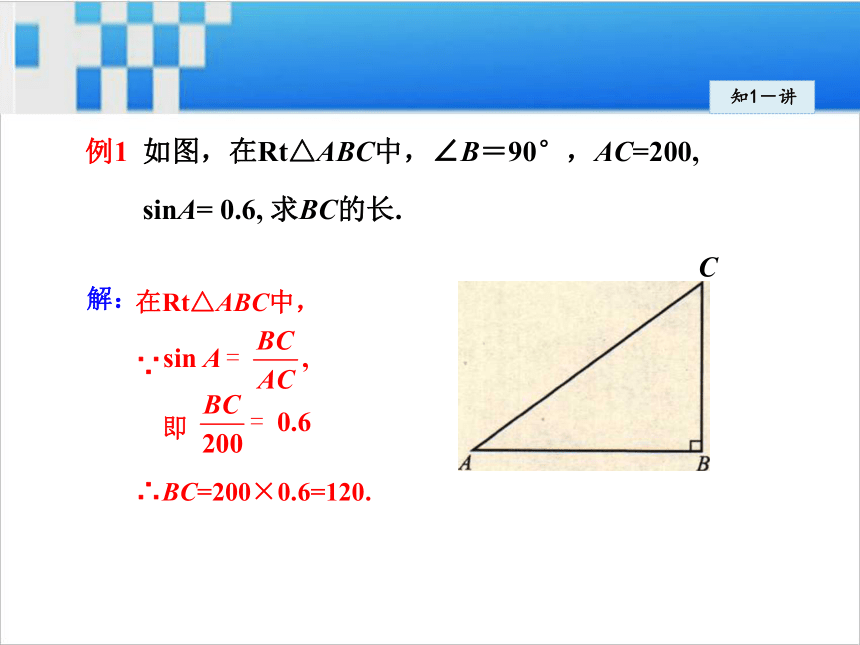
知1-讲例1 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA= 0.6, 求BC的长.知1-讲在Rt△ABC中,
∵
即
∴BC=200×0.6=120.解:C知1-练把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定知1-练(中考·贵阳)在Rt△ABC中,∠C=90°,AC=12, BC=5,则sin A的值为( )
A. B. C. D.
如图,P是α的边OA上一点,点P的坐标为(12,5),
则α的正弦值为( )
A. B.
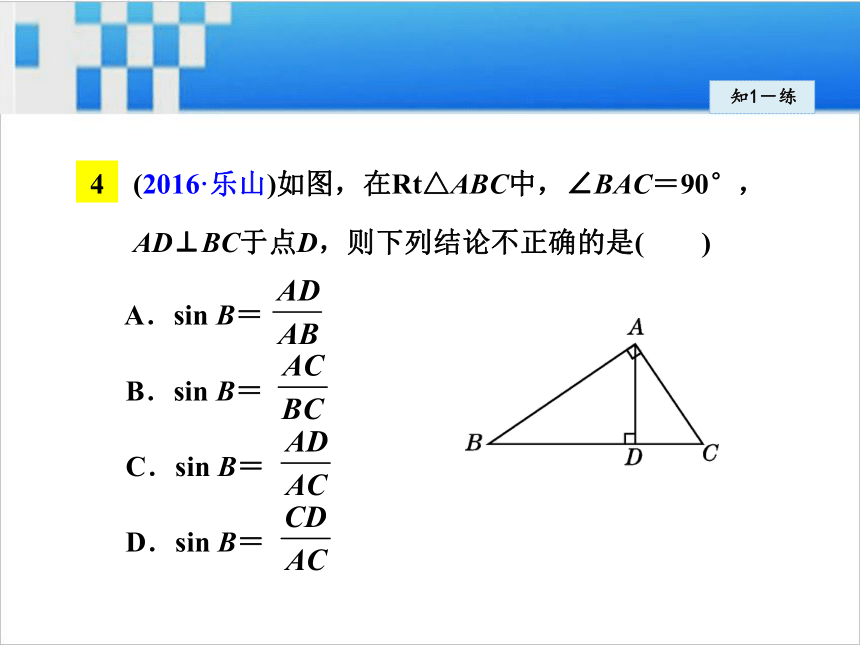
C. D.知1-练(2016·乐山)如图,在Rt△ABC中,∠BAC=90°,
AD⊥BC于点D,则下列结论不正确的是( )
A.sin B=
B.sin B=
C.sin B=
D.sin B=2知识点余弦 余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,
记作cos A,即cos A=知2-讲知2-讲要点精析:正弦、余弦的概念是类比正切得到的,其
本质是两条线段的长度之比,没有单位,其大小只与
角的大小有关,与所在的直角三角形无关.
易错警示:(1)“sin A”“cos A”与“tan A”是整体符号,
符号中省去了“∠”.对于用三个大写字母表示的角
来说,如∠AOB,其正弦应写成“sin∠AOB”,而不
能写成“sin AOB”,余弦、正切也是这样的.
(2)(sin A)2应写成sin2 A,而不能写成sin A2.知2-讲例2 如图,在Rt△ABC中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=知2-讲 在直角三角形中,求锐角的正弦和余弦时,一定
要根据正弦和余弦的定义求解.其中未知边的长度往
往借助勾股定理进行求解.知2-讲例3 如图,在Rt△ABC中,∠C=90°,sin A= BC=40,
求△ABC的周长和面积.
已知BC=40,求△ABC的周长,
则还需要求出其他两边的长,借
助sin A的值可求出AB的长,再
利用勾股定理求出AC的长即可,
直角三角形的面积等于两直角边
长乘积的一半.导引:知2-讲解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC的周长为AB+AC+BC=120,
△ABC的面积为 BC·AC= ×40×30=600.知2-讲正弦的定义表达式sin A= 可根据解题需要变形为
BC=ABsin A或AB=
余弦的定义表达式cos A= 也可变形为
AC=ABcos A或AB= .知2-练在等腰三角形ABC中,AB=AC=5,BC=6,求sinA,cosB,tanB.
在△ABC中,∠C=90°,sinA= BC = 20,
求△ABC的周长和面积.
知2-练(2015·温州)如图,在Rt△ABC中,∠C=90°,
AB=5,BC=3,那么cos A的值等于( )
A. B.
C. D.知2-练(2015·丽水)如图,点A为α边上的任意一点,作
AC⊥BC于点C,CD⊥AB于点D,下列用线段比
表示cos α的值,错误的是( )
A. B.
C. D.知2-练(2016·广东)如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( )
A. B.
C. D.知3-讲3知识点锐角三角函数的取值范围1. 锐角三角函数的定义:
定义:如图,在Rt△ABC中,∠C=90°,∠A,
∠B,∠C的对边分别为a,b,c,则有sin A= ,
cos A= tan A= 我们把sin A,cos A,tan A
叫做∠A的三角函数,即
锐角A的正弦、余弦、正
切叫做∠A的三角函数.要点精析:在锐角三角函数的概念中,∠A是自变量,
其取值范围是0°<∠A<90°.三个比值是因变量,当
∠A确定时,三个比值(正弦、余弦、正切)分别唯一确定,
因此,锐角三角函数是以角为自变量,以比值为因变量
的函数.知3-讲2. 锐角三角函数的取值范围:
在Rt△ABC中,因为各边边长都是正数,且斜边边长
大于直角边边长,所以对于锐角A,有tan A>0,
0<sin A<1,0<cos A<1.
3. 易错警示:
求三角函数值的前提条件是在直角三角形中,遇到锐
角三角形或钝角三角形时一般需要作高构造直角三角
形.知3-讲例4 如图,在Rt△ABC中,∠C=90°,AC=4,
BC=3,求∠A,∠B的三角函数值.
由已知AC与BC的长可确定∠A与∠B的正切,但要
确定∠A与∠B的正弦与余弦,根据定义必须确定
斜边AB的长,这就需要先用勾股定理计算AB的长.
知3-讲 导引:在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴sin A= cos A=
tan A= sin B=
cos B= tan B=知3-讲解:知3-讲求一个直角三角形中锐角的三角函数值时,
①若已知两边长,先根据勾股定理求第三边长,然后根
据概念直接求;
②若已知两边的比,则设辅助未知数表示出两边长,然
后再用方法①求.若α是锐角,sin α=3m-2,则m的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A是方程
(x-0.35)=0的一个根,那么cos A=_______.知3-练1.正弦的定义
2.余弦的定义
3.求锐角三角函数值的三种方法:
(1)在直角三角形里,确定各个边,根据定义直接求出.
(2)利用相似、全等等关系,寻找与所求角相等的角(若
该角的三角函数值知道或者易求).
(3)利用互余的两个角间的特殊关系求.
锐角三角函数的取值范围 2课时流程逐点
导讲练课堂小结作业提升 如图,当Rt△ABC中的锐角A确定时, ∠A的对边与邻边
的比便随之确定.此时,其他边 之间的比也确定吗?与同伴进
行交流.在Rt△ABC中,如果锐角A确定, 那么∠A的对边
与斜边的比、邻边与斜边的比也随之确定. 1知识点正弦 正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
知1-讲例1 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA= 0.6, 求BC的长.知1-讲在Rt△ABC中,
∵
即
∴BC=200×0.6=120.解:C知1-练把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定知1-练(中考·贵阳)在Rt△ABC中,∠C=90°,AC=12, BC=5,则sin A的值为( )
A. B. C. D.
如图,P是α的边OA上一点,点P的坐标为(12,5),
则α的正弦值为( )
A. B.
C. D.知1-练(2016·乐山)如图,在Rt△ABC中,∠BAC=90°,
AD⊥BC于点D,则下列结论不正确的是( )
A.sin B=
B.sin B=
C.sin B=
D.sin B=2知识点余弦 余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,
记作cos A,即cos A=知2-讲知2-讲要点精析:正弦、余弦的概念是类比正切得到的,其
本质是两条线段的长度之比,没有单位,其大小只与
角的大小有关,与所在的直角三角形无关.
易错警示:(1)“sin A”“cos A”与“tan A”是整体符号,
符号中省去了“∠”.对于用三个大写字母表示的角
来说,如∠AOB,其正弦应写成“sin∠AOB”,而不
能写成“sin AOB”,余弦、正切也是这样的.
(2)(sin A)2应写成sin2 A,而不能写成sin A2.知2-讲例2 如图,在Rt△ABC中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=知2-讲 在直角三角形中,求锐角的正弦和余弦时,一定
要根据正弦和余弦的定义求解.其中未知边的长度往
往借助勾股定理进行求解.知2-讲例3 如图,在Rt△ABC中,∠C=90°,sin A= BC=40,
求△ABC的周长和面积.
已知BC=40,求△ABC的周长,
则还需要求出其他两边的长,借
助sin A的值可求出AB的长,再
利用勾股定理求出AC的长即可,
直角三角形的面积等于两直角边
长乘积的一半.导引:知2-讲解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC的周长为AB+AC+BC=120,
△ABC的面积为 BC·AC= ×40×30=600.知2-讲正弦的定义表达式sin A= 可根据解题需要变形为
BC=ABsin A或AB=
余弦的定义表达式cos A= 也可变形为
AC=ABcos A或AB= .知2-练在等腰三角形ABC中,AB=AC=5,BC=6,求sinA,cosB,tanB.
在△ABC中,∠C=90°,sinA= BC = 20,
求△ABC的周长和面积.
知2-练(2015·温州)如图,在Rt△ABC中,∠C=90°,
AB=5,BC=3,那么cos A的值等于( )
A. B.
C. D.知2-练(2015·丽水)如图,点A为α边上的任意一点,作
AC⊥BC于点C,CD⊥AB于点D,下列用线段比
表示cos α的值,错误的是( )
A. B.
C. D.知2-练(2016·广东)如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( )
A. B.
C. D.知3-讲3知识点锐角三角函数的取值范围1. 锐角三角函数的定义:
定义:如图,在Rt△ABC中,∠C=90°,∠A,
∠B,∠C的对边分别为a,b,c,则有sin A= ,
cos A= tan A= 我们把sin A,cos A,tan A
叫做∠A的三角函数,即
锐角A的正弦、余弦、正
切叫做∠A的三角函数.要点精析:在锐角三角函数的概念中,∠A是自变量,
其取值范围是0°<∠A<90°.三个比值是因变量,当
∠A确定时,三个比值(正弦、余弦、正切)分别唯一确定,
因此,锐角三角函数是以角为自变量,以比值为因变量
的函数.知3-讲2. 锐角三角函数的取值范围:
在Rt△ABC中,因为各边边长都是正数,且斜边边长
大于直角边边长,所以对于锐角A,有tan A>0,
0<sin A<1,0<cos A<1.
3. 易错警示:
求三角函数值的前提条件是在直角三角形中,遇到锐
角三角形或钝角三角形时一般需要作高构造直角三角
形.知3-讲例4 如图,在Rt△ABC中,∠C=90°,AC=4,
BC=3,求∠A,∠B的三角函数值.
由已知AC与BC的长可确定∠A与∠B的正切,但要
确定∠A与∠B的正弦与余弦,根据定义必须确定
斜边AB的长,这就需要先用勾股定理计算AB的长.
知3-讲 导引:在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴sin A= cos A=
tan A= sin B=
cos B= tan B=知3-讲解:知3-讲求一个直角三角形中锐角的三角函数值时,
①若已知两边长,先根据勾股定理求第三边长,然后根
据概念直接求;
②若已知两边的比,则设辅助未知数表示出两边长,然
后再用方法①求.若α是锐角,sin α=3m-2,则m的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A是方程
(x-0.35)=0的一个根,那么cos A=_______.知3-练1.正弦的定义
2.余弦的定义
3.求锐角三角函数值的三种方法:
(1)在直角三角形里,确定各个边,根据定义直接求出.
(2)利用相似、全等等关系,寻找与所求角相等的角(若
该角的三角函数值知道或者易求).
(3)利用互余的两个角间的特殊关系求.
