1.2 30°,45°,60°角的三角函数值课件
文档属性
| 名称 | 1.2 30°,45°,60°角的三角函数值课件 |  | |
| 格式 | zip | ||
| 文件大小 | 489.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:40:37 | ||
图片预览







文档简介
课件29张PPT。第一章 直角三角形的边角关系1.2 30°,45°,60°
角的三角函数值1课堂讲解30°,45°,60°角的三角函数值
由特殊三角函数值求角
同角(余角)三角函数间的关系
30°,45°,60°角的三角函数值的实际应用2课时流程逐点
导讲练课堂小结作业提升观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与 同伴进行交流.
(2 ) cos 30° 等于多少? tan 30° 呢?做一做
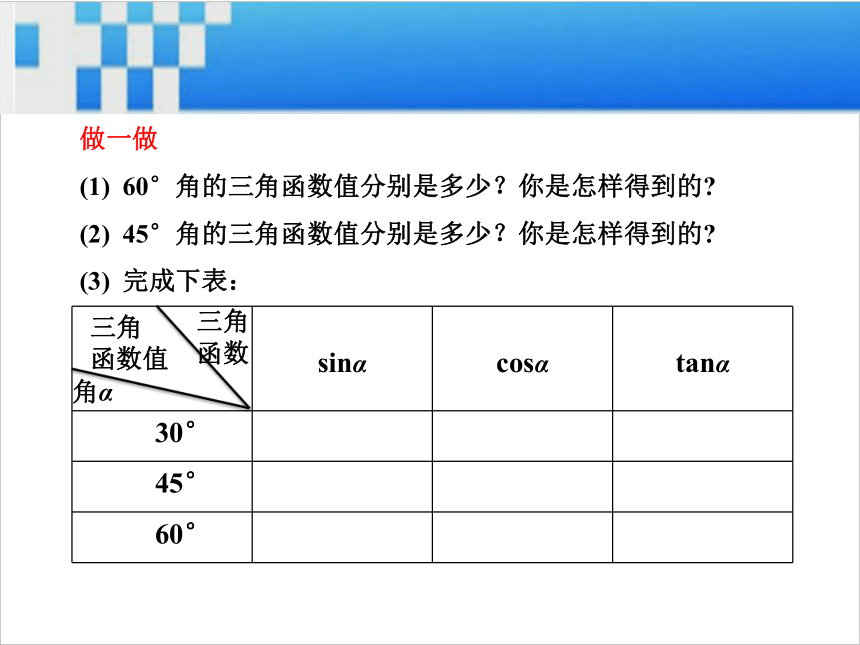
(1) 60°角的三角函数值分别是多少?你是怎样得到的?
(2) 45°角的三角函数值分别是多少?你是怎样得到的?
(3) 完成下表:三角
函数角α三角
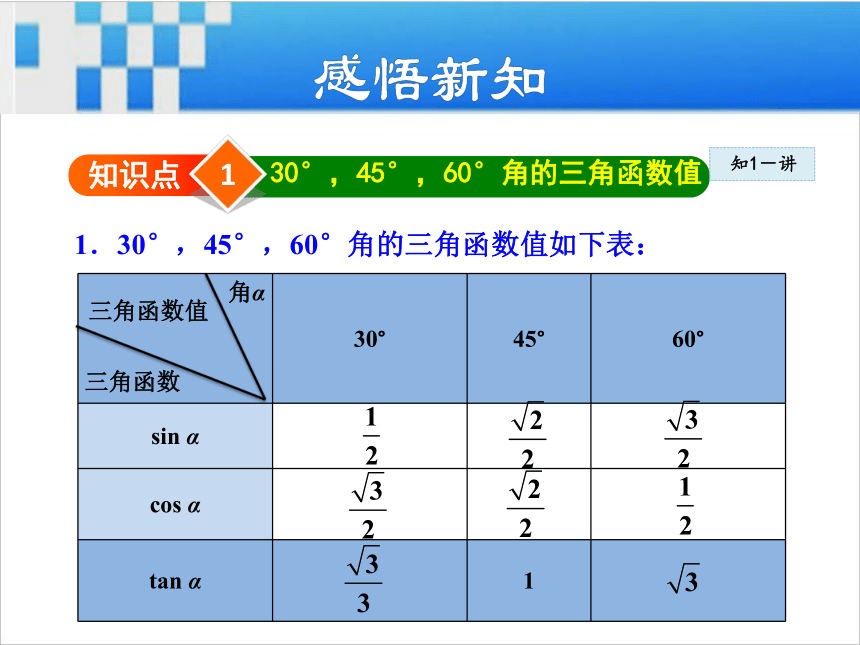
函数值1知识点30°,45°,60°角的三角函数值1.30°,45°,60°角的三角函数值如下表: 知1-讲角α三角函数值三角函数(2) 30°,45°,60°角的三角函数值的记忆方法:
①数形结合记忆法:
如图,常用的一副三角板,记住它们的三边之比:
含30°与60°角的三角板的三边之比为1∶ ∶2;
含45°角的三角板的三边之比为1∶1∶ .
结合三角函数的定义,就
可以很快得出30°,45°,
60°角的三角函数值.
知1-讲②增减规律记忆法:
将30°,45°,60°角的三角函数值表反复背诵,根据
这些数据与它们所处位置的规律进行记忆.30°,45°,
60°角的正弦、余弦值可以看作是形如“ ”的形式,
只是被开方数不同,由左至右正弦的被开方数是按1,2,
3的顺序,余弦的被开方数则按3,2,1的顺序;对于
30°,45°,60°角的正切,中间是1,左边是1除以
右边是1乘 .知1-讲例1 计算:
(1)sin 30° + cos 45° ;
(2) sin260°+ cos260° — tan 45°.
(1) sin 30。+ cos 45。 =
(2) sin260° + cos260° - tan 45°
知1-讲解:知1-练计算:
(1) sin 60。— tan 45。;
(2) cos 60° + tan 60° ;
(3) sin 45° + sin 60° — 2 cos 45°.知1-练2 (2016·天津)sin 60°的值等于( )
A. B. C. D.
3 (2015·滨州)下列运算:sin 30°= ,
π0=π,2-2=-4,其中运算结果正确的个数
为( )
A.4 B.3 C.2 D.1知1-练4 (中考·包头)计算sin245°+cos 30°·tan 60°,其
结果是( )
A.2 B.1 C. D.
5 菱形OABC在平面直角坐标系中的位置如图所示,
∠AOC=45°,OC= ,则点B的坐标为( )
A.( ,1) B.(1, )
C.( +1,1) D.(1, +1)2知识点由特殊三角函数值求角 通过该表可以方便地知道30°,45°,60°角的
三角函数值.它的另一个应用:如果已知一个锐角的
三角函数值,就可以求出这个锐角的度数.例如:若
sin θ= ,则锐角θ=45°.知2-讲知2-讲例2 在Rt△ABC中,∠C=90°,cos A= 求∠A,
∠B的度数.
导引:利用特殊角的三角函数值,查找值所对应的角,再
利用直角三角形两锐角互余的性质求出∠B.
解:∵cos A= cos 30°=
∴∠A=30°.
∴∠B=90°-30°=60°.知2-讲 在运用数形结合记忆法或增减规律记忆法记住特
殊角的三角函数值后,很容易确定∠A的度数,从而
可用两锐角互余的关系计算∠B.知2-练(2015·酒泉)已知α,β均为锐角,且满足
+ =0,则α+β=________.
(2015·庆阳)在△ABC中,若角A,B满足|cos A- |
+(1-tan B)2=0,则∠C的大小是( )
A.45° B.60° C.75° D.105°
知2-练在△ABC中,∠A,∠B都是锐角,且sin A=
cos B= 则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定知3-讲3知识点同角(余角)三角函数间的关系拓展:
如图,在Rt△ABC中,∠C=90°,∠A,∠B,
∠C的对边分别为a,b,c,令∠A=α.
(1)同角三角函数之间的关系.
①平方关系:sin2 α+cos2 α=1.
②商关系:∵
且tan α= ∴ =tan α.(2)互余两角的三角函数的关系.∵sin A= cos B=
∴sin A=cos B.同理cos A=sin B.又∵∠A+∠B=90°,
即∠B=90°-∠A,∴sin A=cos B=cos (90°-∠A),
cos A=sin B=sin (90°-∠A).即任意锐角的正弦值等于它
的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值.
∵tan A= tan B= ∴tan A·tan B=1.此结论适用于两
个角互为余角的情况,它们并不一定是同一直角三角形中的
两个锐角.知3-讲例3 已知α为锐角,且cos α= 求 的值.
运用同角三角函数的关系,由cos α的值可求得sin α
及tan α 的值,然后代入计算即可.知3-讲 导引:由sin2α+cos2α=1,sin α>0,得sin α=
而cos α= 所以sin α=
因为 =tan α,所以tan α=
故知3-讲解:知3-讲 灵活运用同角或互余两角的三角函数的关系.在
正弦、余弦、正切中,某锐角的一种三角函数值已知,
则可算出另两种三角函数值.本题另有两法:①参数法,
即由cos α= 可设在Rt△ABC中,∠C=90°,∠A
=α,AC=k,AB=3k,由勾股定理得BC= k,
从而求得sin α与tan α的值,再代入求解;知3-讲②定义法,即设在Rt△ABC中,∠C=90°,a,b,c分
别是∠A,∠B,∠C的对边,∠A=α,则由定义得
而a2+b2=c2,
故原式=
一般来说,参数法与定义法更常用.已知α为锐角,m=sin2α+cos2α,则( )
A.m>1 B.m=1 C.m<1 D.m≥1
在Rt△ABC中,∠C=90°,若cos B= 则sin B
的值是( )
A. B. C. D.知3-练3 在Rt△ABC中,∠C=90°,sin B= 则cos A
的值为( )
A. B. C. D.知3-练知4-讲4知识点30°45°60°角的三角函数值的实际应用用三角函数解应用题的一般步骤为:
(1)根据实际问题,构造直角三角形,建立三角函数模
型;
(2)利用三角函数的定义或定义的变形表示题目中相关
的量;
(3)找出各个量之间的关系;
(4)利用已知量与未知量的关系求出未知量.例4 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向
两边摆动时, 摆角恰好为60°,且两边的摆动角度相
同,求它摆至最高位置时与其摆至最低 位置时的高度
之差(结果精确到0.01 m).
解:如图,根据题意可知,
∠AOD= 60°=30°,OD=2.5m,
∴OC=ODcos30°=2.5× ≈2.165(m).
∴AC=2.5-2.165≈0.34(m)
所以,最高位置与最低位置的高度差约为0.34m.知4-讲知4-讲 利用特殊角的三角函数值解决实际问题要了解角之
间的关系,找到与已知和未知相关联的直角三角形,当
图形中没有直角三角形时,要通过作高或垂线构造直角
三角形.当问题以一个实际问题的形式给出时,要善于
读懂题意,把实际问题化归为直角三角形中边角关系的
问题加以解决.某商场有以自动扶梯,其倾斜角为30°,高为7m.
扶梯的长度是多少?知4-练这节课我的收获是什么?有什么经验与同学们分享?
角的三角函数值1课堂讲解30°,45°,60°角的三角函数值
由特殊三角函数值求角
同角(余角)三角函数间的关系
30°,45°,60°角的三角函数值的实际应用2课时流程逐点
导讲练课堂小结作业提升观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与 同伴进行交流.
(2 ) cos 30° 等于多少? tan 30° 呢?做一做
(1) 60°角的三角函数值分别是多少?你是怎样得到的?
(2) 45°角的三角函数值分别是多少?你是怎样得到的?
(3) 完成下表:三角
函数角α三角
函数值1知识点30°,45°,60°角的三角函数值1.30°,45°,60°角的三角函数值如下表: 知1-讲角α三角函数值三角函数(2) 30°,45°,60°角的三角函数值的记忆方法:
①数形结合记忆法:
如图,常用的一副三角板,记住它们的三边之比:
含30°与60°角的三角板的三边之比为1∶ ∶2;
含45°角的三角板的三边之比为1∶1∶ .
结合三角函数的定义,就
可以很快得出30°,45°,
60°角的三角函数值.
知1-讲②增减规律记忆法:
将30°,45°,60°角的三角函数值表反复背诵,根据
这些数据与它们所处位置的规律进行记忆.30°,45°,
60°角的正弦、余弦值可以看作是形如“ ”的形式,
只是被开方数不同,由左至右正弦的被开方数是按1,2,
3的顺序,余弦的被开方数则按3,2,1的顺序;对于
30°,45°,60°角的正切,中间是1,左边是1除以
右边是1乘 .知1-讲例1 计算:
(1)sin 30° + cos 45° ;
(2) sin260°+ cos260° — tan 45°.
(1) sin 30。+ cos 45。 =
(2) sin260° + cos260° - tan 45°
知1-讲解:知1-练计算:
(1) sin 60。— tan 45。;
(2) cos 60° + tan 60° ;
(3) sin 45° + sin 60° — 2 cos 45°.知1-练2 (2016·天津)sin 60°的值等于( )
A. B. C. D.
3 (2015·滨州)下列运算:sin 30°= ,
π0=π,2-2=-4,其中运算结果正确的个数
为( )
A.4 B.3 C.2 D.1知1-练4 (中考·包头)计算sin245°+cos 30°·tan 60°,其
结果是( )
A.2 B.1 C. D.
5 菱形OABC在平面直角坐标系中的位置如图所示,
∠AOC=45°,OC= ,则点B的坐标为( )
A.( ,1) B.(1, )
C.( +1,1) D.(1, +1)2知识点由特殊三角函数值求角 通过该表可以方便地知道30°,45°,60°角的
三角函数值.它的另一个应用:如果已知一个锐角的
三角函数值,就可以求出这个锐角的度数.例如:若
sin θ= ,则锐角θ=45°.知2-讲知2-讲例2 在Rt△ABC中,∠C=90°,cos A= 求∠A,
∠B的度数.
导引:利用特殊角的三角函数值,查找值所对应的角,再
利用直角三角形两锐角互余的性质求出∠B.
解:∵cos A= cos 30°=
∴∠A=30°.
∴∠B=90°-30°=60°.知2-讲 在运用数形结合记忆法或增减规律记忆法记住特
殊角的三角函数值后,很容易确定∠A的度数,从而
可用两锐角互余的关系计算∠B.知2-练(2015·酒泉)已知α,β均为锐角,且满足
+ =0,则α+β=________.
(2015·庆阳)在△ABC中,若角A,B满足|cos A- |
+(1-tan B)2=0,则∠C的大小是( )
A.45° B.60° C.75° D.105°
知2-练在△ABC中,∠A,∠B都是锐角,且sin A=
cos B= 则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定知3-讲3知识点同角(余角)三角函数间的关系拓展:
如图,在Rt△ABC中,∠C=90°,∠A,∠B,
∠C的对边分别为a,b,c,令∠A=α.
(1)同角三角函数之间的关系.
①平方关系:sin2 α+cos2 α=1.
②商关系:∵
且tan α= ∴ =tan α.(2)互余两角的三角函数的关系.∵sin A= cos B=
∴sin A=cos B.同理cos A=sin B.又∵∠A+∠B=90°,
即∠B=90°-∠A,∴sin A=cos B=cos (90°-∠A),
cos A=sin B=sin (90°-∠A).即任意锐角的正弦值等于它
的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值.
∵tan A= tan B= ∴tan A·tan B=1.此结论适用于两
个角互为余角的情况,它们并不一定是同一直角三角形中的
两个锐角.知3-讲例3 已知α为锐角,且cos α= 求 的值.
运用同角三角函数的关系,由cos α的值可求得sin α
及tan α 的值,然后代入计算即可.知3-讲 导引:由sin2α+cos2α=1,sin α>0,得sin α=
而cos α= 所以sin α=
因为 =tan α,所以tan α=
故知3-讲解:知3-讲 灵活运用同角或互余两角的三角函数的关系.在
正弦、余弦、正切中,某锐角的一种三角函数值已知,
则可算出另两种三角函数值.本题另有两法:①参数法,
即由cos α= 可设在Rt△ABC中,∠C=90°,∠A
=α,AC=k,AB=3k,由勾股定理得BC= k,
从而求得sin α与tan α的值,再代入求解;知3-讲②定义法,即设在Rt△ABC中,∠C=90°,a,b,c分
别是∠A,∠B,∠C的对边,∠A=α,则由定义得
而a2+b2=c2,
故原式=
一般来说,参数法与定义法更常用.已知α为锐角,m=sin2α+cos2α,则( )
A.m>1 B.m=1 C.m<1 D.m≥1
在Rt△ABC中,∠C=90°,若cos B= 则sin B
的值是( )
A. B. C. D.知3-练3 在Rt△ABC中,∠C=90°,sin B= 则cos A
的值为( )
A. B. C. D.知3-练知4-讲4知识点30°45°60°角的三角函数值的实际应用用三角函数解应用题的一般步骤为:
(1)根据实际问题,构造直角三角形,建立三角函数模
型;
(2)利用三角函数的定义或定义的变形表示题目中相关
的量;
(3)找出各个量之间的关系;
(4)利用已知量与未知量的关系求出未知量.例4 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向
两边摆动时, 摆角恰好为60°,且两边的摆动角度相
同,求它摆至最高位置时与其摆至最低 位置时的高度
之差(结果精确到0.01 m).
解:如图,根据题意可知,
∠AOD= 60°=30°,OD=2.5m,
∴OC=ODcos30°=2.5× ≈2.165(m).
∴AC=2.5-2.165≈0.34(m)
所以,最高位置与最低位置的高度差约为0.34m.知4-讲知4-讲 利用特殊角的三角函数值解决实际问题要了解角之
间的关系,找到与已知和未知相关联的直角三角形,当
图形中没有直角三角形时,要通过作高或垂线构造直角
三角形.当问题以一个实际问题的形式给出时,要善于
读懂题意,把实际问题化归为直角三角形中边角关系的
问题加以解决.某商场有以自动扶梯,其倾斜角为30°,高为7m.
扶梯的长度是多少?知4-练这节课我的收获是什么?有什么经验与同学们分享?
