1.5.1 解直角三角形在实际中的一般应用课件
文档属性
| 名称 | 1.5.1 解直角三角形在实际中的一般应用课件 |  | |
| 格式 | zip | ||
| 文件大小 | 399.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:42:08 | ||
图片预览







文档简介
课件25张PPT。第一章 直角三角形的边角关系1.5 三角函数的应用第1课时 解直角三角形在实
际中的一般应用1课堂讲解方位角
借助工具测量的应用
借助影子测量的应用2课时流程逐点
导讲练课堂小结作业提升 如图1 - 13,海中有一个小岛A,该岛四周10nmile内有暗
礁.今有货轮 由西向东航行,开始在A岛南偏西55°的B处,
往东行驶20 n mile后到达该岛的南偏西25°的C处.之后,货
轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是
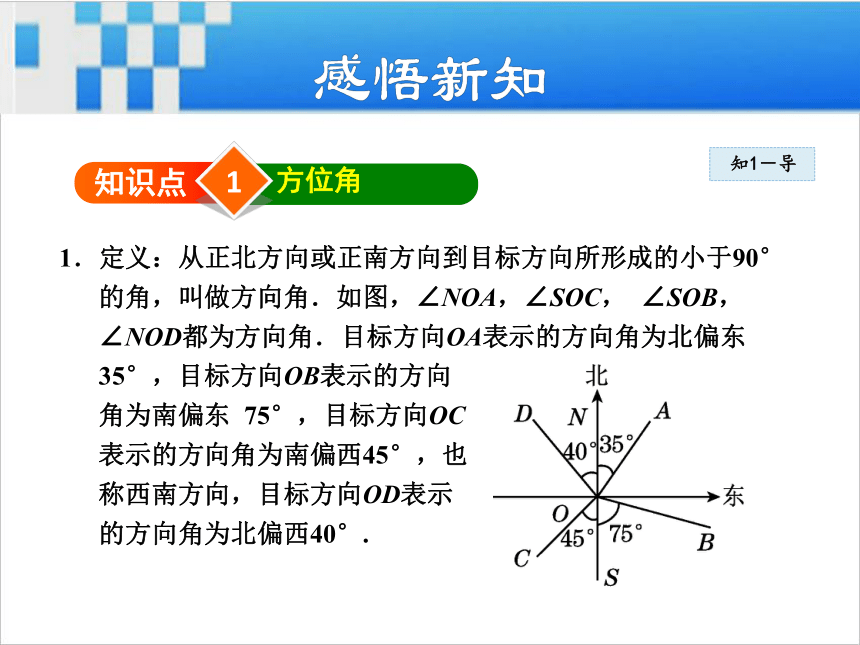
怎样想的?与同伴 进行交流.1知识点方位角1.定义:从正北方向或正南方向到目标方向所形成的小于90°
的角,叫做方向角.如图,∠NOA,∠SOC, ∠SOB,
∠NOD都为方向角.目标方向OA表示的方向角为北偏东
35°,目标方向OB表示的方向
角为南偏东 75°,目标方向OC
表示的方向角为南偏西45°,也
称西南方向,目标方向OD表示
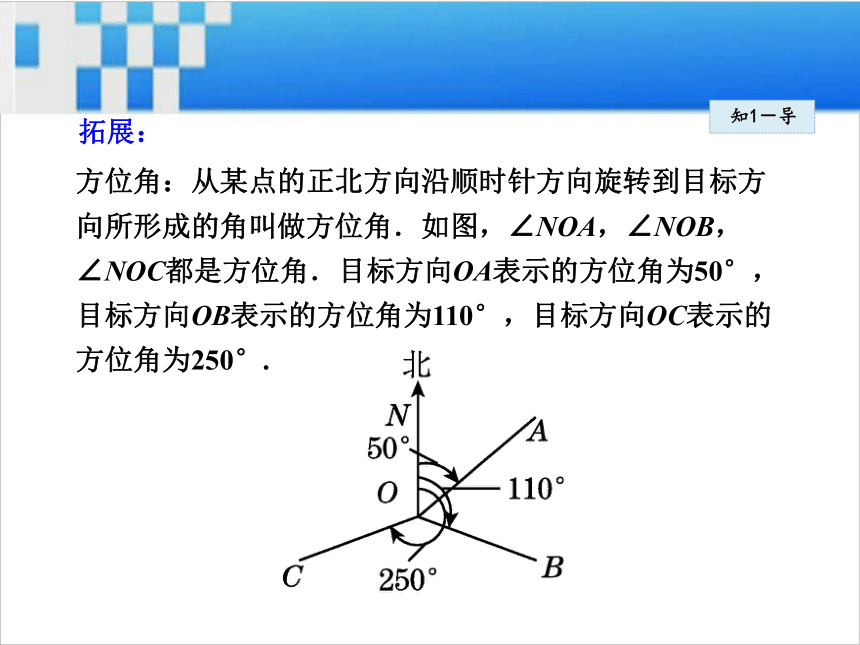
的方向角为北偏西40°.知1-导方位角:从某点的正北方向沿顺时针方向旋转到目标方
向所形成的角叫做方位角.如图,∠NOA,∠NOB,
∠NOC都是方位角.目标方向OA表示的方位角为50°,
目标方向OB表示的方位角为110°,目标方向OC表示的
方位角为250°.知1-导拓展:(1)方向角通常是以南北方向线为主,分南偏和北偏
(东、西).
(2)观测点不同,所得的方向角不同.知1-导2. 易错警示:例1 一轮船以15 n mile/h的速度向正东方向航行,上午8时,
该船在A处测得灯塔B位于它的北偏东30°方向,上午
10时行至C处,测得灯塔B恰好在它的正北方向,此时
它与灯塔的距离是多少?知1-讲灯塔B位于A的北偏东30°方向,指的是∠DAB=30°.
由于对方向角的错误认识,导致错解.错解分析:知1-讲如图,由题意知在△ABC中,∠BCA=90°,
∠BAC=90°-∠BAD=90°-30°=60°,
AC=15×2=30(n mile),
∴BC=AC·tan 60°=30× =30 (n mile).
即此时它与灯塔的距离是30 n mile.解:某年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位.一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,继续向东航行100 m,到达B处后测得航标C在北偏东45°方向上,如图所示.现已知以航标C为圆心,以120 m为半径的圆形区域内有浅滩,如果这条船继续前进,是否有搁浅的危险?( ≈1.732)知1-练2知识点借助工具测量的应用知2-讲想一想
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测
得仰角为30°,再往塔的方向前 进50m至B处,测得仰角
为60°,那么该塔有多 高?(小明的身高忽略不计,结
果精确到1m)知2-讲1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要
解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.知2-讲2、常见的图形与关系式如下表所示:知2-讲续表:知2-讲例2〈益阳〉“中国益阳”网上消息,益阳市为了改善市区交通
状况,计划在康富路的北端修建通往资江北岸的新大桥.
如图,新大桥的两端位于A,B两点,小张为了测量A,B
之间的河宽,在垂直于新大桥AB的直线形道路l上测得如下
数据:∠BDA=76.1°,∠BCA=68.2°,CD=82 m.求
AB的长.(结果精确到0.1 m.
参考数据:sin 76.1°≈0.97,
cos 76.1°≈0.24,tan 76.1°≈4.0;
sin 68.2°≈0.93,cos 68.2°≈0.37,
tan 68.2°≈2.5)知2-讲设AD=x m,在Rt△ABC中,利用∠BCA的正切值,
可以用含x的代数式表示AB.同理在Rt△ABD中,利
用∠BDA的正切值表示出AB,从而列出关于x的方程,
求出x的值就能求出AB的长了.导引:知2-讲 设AD=x m,则AC=(x+82) m.
在Rt△ABC中,tan ∠BCA=
∴AB=AC·tan ∠BCA=(x+82)tan 68.2° m.
在Rt△ABD中,tan ∠BDA=
∴AB=AD·tan ∠BDA=xtan 76.1° m.
∴(x+82)tan 68.2°=xtan 76.1°.∴x≈136.67.
∴AB≈4×136.67≈546.7(m).
即AB的长约为546.7 m.解:知2-讲 解直角三角形的应用问题,需要把实际问题转化为
数学模型来解决.解决直角三角形有关的应用题最常用
的方法是画图(包括作辅助线,构造直角三角形或特殊平
行四边形),根据所给数据,选用恰当的锐角三角函数求
出有关的量或用含有未知数的式子表示有关的量进行求
解.警示点:(1)注意方程思想的运用;(2)注意结果必须
根据题目要求进行保留.长为4 m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了________.知2-练知2-练(2016·益阳)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1 m,则旗杆PA的高度为( )
A. B.
C. D.知3-讲3知识点借助影子测量的应用例3 如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且
AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在
台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
问小猫还能否晒到太阳?
请说明理由.(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
知3-讲解: ∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
知3-讲如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,则电线杆AB的长为________.知3-练(2015·绵阳)如图,要在宽为22 m的九州大道两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2 ) m
B.(11 -2 ) m
C.(11-2 ) m
D.(11 -4) m知3-练利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
注意:当有些图形不是直角三角形时,可考虑适当添加
辅助线构造直角三角形或其他特殊的四边形得出.
际中的一般应用1课堂讲解方位角
借助工具测量的应用
借助影子测量的应用2课时流程逐点
导讲练课堂小结作业提升 如图1 - 13,海中有一个小岛A,该岛四周10nmile内有暗
礁.今有货轮 由西向东航行,开始在A岛南偏西55°的B处,
往东行驶20 n mile后到达该岛的南偏西25°的C处.之后,货
轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?你是
怎样想的?与同伴 进行交流.1知识点方位角1.定义:从正北方向或正南方向到目标方向所形成的小于90°
的角,叫做方向角.如图,∠NOA,∠SOC, ∠SOB,
∠NOD都为方向角.目标方向OA表示的方向角为北偏东
35°,目标方向OB表示的方向
角为南偏东 75°,目标方向OC
表示的方向角为南偏西45°,也
称西南方向,目标方向OD表示
的方向角为北偏西40°.知1-导方位角:从某点的正北方向沿顺时针方向旋转到目标方
向所形成的角叫做方位角.如图,∠NOA,∠NOB,
∠NOC都是方位角.目标方向OA表示的方位角为50°,
目标方向OB表示的方位角为110°,目标方向OC表示的
方位角为250°.知1-导拓展:(1)方向角通常是以南北方向线为主,分南偏和北偏
(东、西).
(2)观测点不同,所得的方向角不同.知1-导2. 易错警示:例1 一轮船以15 n mile/h的速度向正东方向航行,上午8时,
该船在A处测得灯塔B位于它的北偏东30°方向,上午
10时行至C处,测得灯塔B恰好在它的正北方向,此时
它与灯塔的距离是多少?知1-讲灯塔B位于A的北偏东30°方向,指的是∠DAB=30°.
由于对方向角的错误认识,导致错解.错解分析:知1-讲如图,由题意知在△ABC中,∠BCA=90°,
∠BAC=90°-∠BAD=90°-30°=60°,
AC=15×2=30(n mile),
∴BC=AC·tan 60°=30× =30 (n mile).
即此时它与灯塔的距离是30 n mile.解:某年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位.一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,继续向东航行100 m,到达B处后测得航标C在北偏东45°方向上,如图所示.现已知以航标C为圆心,以120 m为半径的圆形区域内有浅滩,如果这条船继续前进,是否有搁浅的危险?( ≈1.732)知1-练2知识点借助工具测量的应用知2-讲想一想
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测
得仰角为30°,再往塔的方向前 进50m至B处,测得仰角
为60°,那么该塔有多 高?(小明的身高忽略不计,结
果精确到1m)知2-讲1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要
解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.知2-讲2、常见的图形与关系式如下表所示:知2-讲续表:知2-讲例2〈益阳〉“中国益阳”网上消息,益阳市为了改善市区交通
状况,计划在康富路的北端修建通往资江北岸的新大桥.
如图,新大桥的两端位于A,B两点,小张为了测量A,B
之间的河宽,在垂直于新大桥AB的直线形道路l上测得如下
数据:∠BDA=76.1°,∠BCA=68.2°,CD=82 m.求
AB的长.(结果精确到0.1 m.
参考数据:sin 76.1°≈0.97,
cos 76.1°≈0.24,tan 76.1°≈4.0;
sin 68.2°≈0.93,cos 68.2°≈0.37,
tan 68.2°≈2.5)知2-讲设AD=x m,在Rt△ABC中,利用∠BCA的正切值,
可以用含x的代数式表示AB.同理在Rt△ABD中,利
用∠BDA的正切值表示出AB,从而列出关于x的方程,
求出x的值就能求出AB的长了.导引:知2-讲 设AD=x m,则AC=(x+82) m.
在Rt△ABC中,tan ∠BCA=
∴AB=AC·tan ∠BCA=(x+82)tan 68.2° m.
在Rt△ABD中,tan ∠BDA=
∴AB=AD·tan ∠BDA=xtan 76.1° m.
∴(x+82)tan 68.2°=xtan 76.1°.∴x≈136.67.
∴AB≈4×136.67≈546.7(m).
即AB的长约为546.7 m.解:知2-讲 解直角三角形的应用问题,需要把实际问题转化为
数学模型来解决.解决直角三角形有关的应用题最常用
的方法是画图(包括作辅助线,构造直角三角形或特殊平
行四边形),根据所给数据,选用恰当的锐角三角函数求
出有关的量或用含有未知数的式子表示有关的量进行求
解.警示点:(1)注意方程思想的运用;(2)注意结果必须
根据题目要求进行保留.长为4 m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了________.知2-练知2-练(2016·益阳)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1 m,则旗杆PA的高度为( )
A. B.
C. D.知3-讲3知识点借助影子测量的应用例3 如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且
AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在
台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
问小猫还能否晒到太阳?
请说明理由.(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
知3-讲解: ∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
知3-讲如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,则电线杆AB的长为________.知3-练(2015·绵阳)如图,要在宽为22 m的九州大道两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2 ) m
B.(11 -2 ) m
C.(11-2 ) m
D.(11 -4) m知3-练利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
注意:当有些图形不是直角三角形时,可考虑适当添加
辅助线构造直角三角形或其他特殊的四边形得出.
