2.1.3 垂线段及其性质课件

课件26张PPT。第3课时 垂线段及其
性质第二章 相交线与平行线2.1 两条直线的位置关系1课堂讲解垂线段的意义
垂线段的性质
点到直线的距离2课时流程逐点
导讲练课堂小结作业提升1.垂线的定义是什么？
2.画垂线的步骤有哪些？
3.垂线的性质 1 的内容是什么？复习回顾1知识点垂线段的意义 知1－导想一想
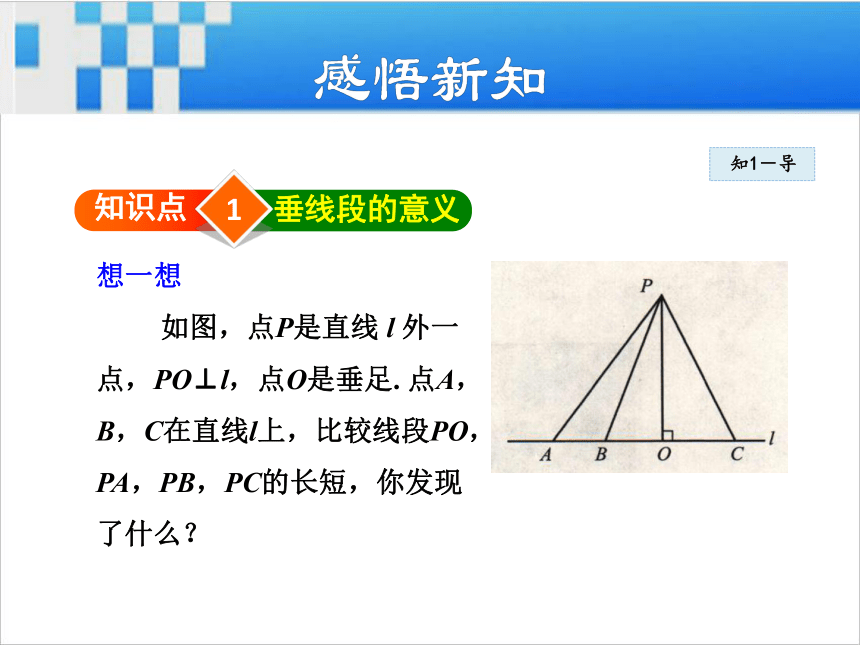
如图，点P是直线 l 外一
点，PO⊥l，点O是垂足. 点A，
B，C在直线l上，比较线段PO，
PA，PB，PC的长短，你发现
了什么？知1－讲垂线段的意义：
过直线外一点画已知直线的垂线，这点与垂足
之间的线段，叫这点到已知直线的垂线段.知1－练1　下列说法正确的是(　　)
A．垂线段就是垂直于已知直线的线段
B．垂线段就是垂直于已知直线并且与已知直线相交的线段
C．垂线段是一条竖起来的线段
D．过直线外一点向该直线作垂线，这一点到垂足之间的线段叫垂线段知1－练2　如图，下列说法不正确的是(　　)
A．点B到AC的垂线段是线段AB
B．点C到AB的垂线段是线段AC
C．线段AD是点D到BC的垂线段
D．线段BD是点B到AD的垂线段 2知识点垂线段的性质 知2－讲1.垂直的性质2：
直线外一点与直线上各点连接的所有线段中，垂线段最
短．简单说成：垂线段最短．
2.垂线、垂直与垂线段的关系：
(1)区别：垂线是一条与已知直线垂直的直线；垂直是两
条直线之间的位置关系；垂线段是一条与已知直线垂
直的线段．
(2)联系：垂线段所在的直线是已知直线的垂线；垂线段
所在的直线与已知直线垂直．知2－讲例1 如图，AB是一条河流，要铺设管道将河水引到C，D
两个用水点，现有两种铺设管道的方案：
方案一：分别过点C，D作AB的
垂线，垂足分别为点E，F，沿
CE，DF铺设管道；
方案二：连接CD交AB于点P，
沿PC，PD铺设管道.
这两种铺设管道的方案哪一种更节省材料？为什么？
(河流的宽度可忽略不计)知2－讲要尽可能节省材料，也就是让管道的总长度更小．
方案一中CE，DF是垂线段，而方案二中PC，PD
不是垂线段，所以CE＜PC，DF＜PD.所以CE＋DF
＜PC＋PD.所以方案一更节省材料．导引：按方案一铺设管道更节省材料．理由如下：
因为CE⊥AB，DF⊥AB，CD不垂直于AB，
且根据“垂线段最短”可知，CE＜PC，DF＜PD，
所以CE＋DF＜PC＋PD.
所以沿CE，DF铺设管道更节省材料．解： 本题主要利用“垂线段最短”来解决实际问题，
解决这类求最短距离问题时，要注意“垂线段最短”
与“两点之间，线段最短”的区别，辨明这两条性
质的应用条件：点到直线的最短距离，两点间的最
短距离．知2－讲1　如图，计划在河边建一水厂，过C点作CD⊥AB于D点．在D点建水厂，可使水厂到村庄C的路程最短，这样设计的依据是____________________．知2－练2　如图，在铁路旁有一李庄，现要建一火车站，为了
使李庄人乘车最方便，请你在铁路线上选一点来
建火车站，应建在(　　)
A．A点
B．B点
C．C点
D．D点知2－练3　如图，已知AC⊥BC，CD⊥AB，垂足分别是C，
D，那么以下线段大小的比较必定成立的是(　　)
A．CD＞AD
B．AC＜BC
C．BC＞BD
D．CD＜BD知2－练4　如图，在三角形ABC中，∠C＝90°，AC＝3，点
P可以在直线BC上自由移动，则AP的长不可能
是(　　)
A．2.5　　　
B．3　　　
C．4　　　
D．5知2－练3知识点点到直线的距离知3－导 如图，过点A作l的垂线，垂足为B，线段AB的长
度叫做点A到直线l的距离.知3－导议一议
你知道体育课上老师是怎样测量跳远成绩的吗？
你能说说其中的道理吗? 知3－讲1.点到直线的距离：直线外一点到这条直线的垂线段的
长度，叫做点到直线的距离．
要点精析：
(1)因为某点到已知直线的垂线段只有一条，所以点到
直线的距离是唯一的；
(2)当这个点在已知直线上时，可看作点到直线的距离
为0.
2.易错警示：点到直线的距离是指垂线段的长度，而不
是垂线段．知3－讲例2 点P为直线m外一点，点A，B，C为直线m上三点，PA＝4 cm，PB＝5 cm，PC＝2 cm，则点P到直线m的距离(　　)
A．等于4 cm　 　B．等于2 cm　　
C．小于2 cm　　 D．不大于2 cm点到直线的距离是该点到这条直线的垂线段的长度，
而垂线段是该点与直线上各点的连线中最短的．从条
件看，PC是三条线段中最短的，但不一定是所有连线
中最短的，所以点P到直线m的距离应该是不大于2 cm.导引：D知3－讲例3 如图，在三角形ABC中，∠ACB＝90°，CD⊥AB，垂足为D.若AC＝4 cm，BC＝3 cm，AB＝5 cm，则点A到直线BC的距离为________，点B到直线AC的距离为______，点C到直线AB的距离为______．根据点到直线的距离的定义可知，
点A到直线BC的距离是线段AC的长，
点B到直线AC的距离是线段BC的长，点C到直线AB的距
离是线段CD的长．因为三角形ABC的面积S＝ AC·BC＝
AB·CD，所以AC·BC＝AB·CD，进而可得CD＝2.4 cm.导引：4 cm3 cm2.4 cm 正确理解点到直线的距离及两点间的距离是解
决此类问题的关键．解决此类问题应注意：(1)点到
直线的距离是点到直线的垂线段的长度，而不是垂
线，也不是垂线段；(2)距离表示线段的长度，是一
个数量，与线段不能等同；(3)用垂线段的长度表示
点到直线的距离，其实质是点与垂足两点间的距离，
体现了数形结合思想．知3－讲1　如图是小凡同学在体育课上跳远后留下的脚印，他的跳远成绩是线段________的长度．知3－练2　下列图形中，线段PQ的长表示点P到直线MN的距离的是(　　)知3－练3　点到直线的距离是指(　　)
A．直线外一点到这条直线的垂线的长度
B．直线外一点到这条直线上的任意一点的距离
C．直线外一点到这条直线的垂线段
D．直线外一点到这条直线的垂线段的长度知3－练4　如图，AB⊥AC，AD⊥BC，如果AB＝4 cm，AC＝3 cm，AD＝2.4 cm，那么点C到直线AB的距离为(　　)
A．3 cm
B．4 cm
C．2.4 cm
D．无法确定知3－练1.垂线段的定义：过直线外一点画已知直线的垂线，这
点与垂足之间的线段，叫这点到已知直线的垂线段.
2.垂线段的性质：垂线段最短.
3.点到直线的距离：直线外一点到这条直线的垂线段的
长度，叫做点到直线的距离．