2.2.2 用“内错角、同旁内角”判定平行线 课件
文档属性
| 名称 | 2.2.2 用“内错角、同旁内角”判定平行线 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 21:17:44 | ||
图片预览









文档简介
课件45张PPT。第2课时 用“内错角、同
旁内角”判定
平行线第二章 相交线与平行线2.2 探索直线平行的条件1课堂讲解内错角
同旁内角
内错角相等,两直线平行
同旁内角互补,两直线平行2课时流程逐点
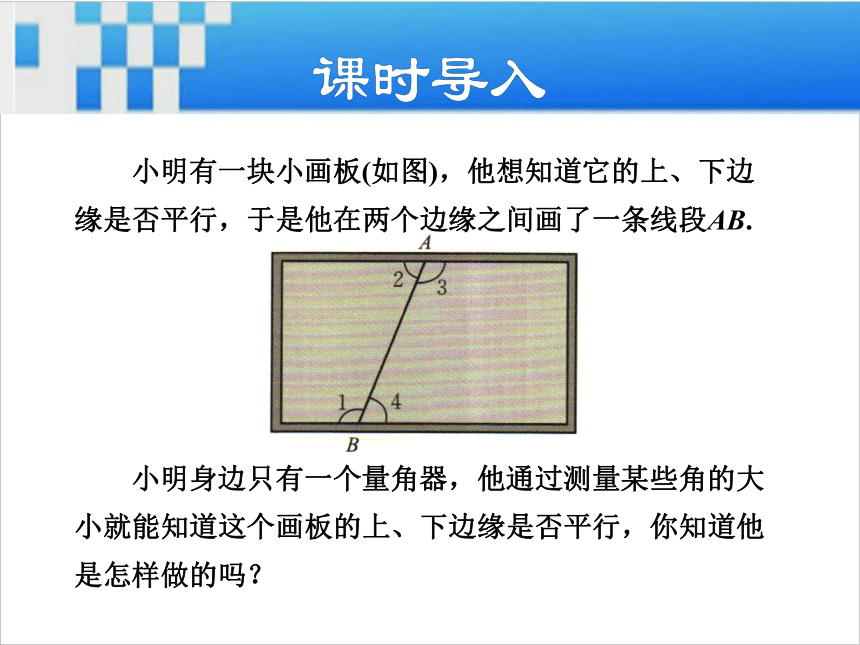
导讲练课堂小结作业提升 小明有一块小画板(如图),他想知道它的上、下边
缘是否平行,于是他在两个边缘之间画了一条线段AB. 小明身边只有一个量角器,他通过测量某些角的大
小就能知道这个画板的上、下边缘是否平行,你知道他
是怎样做的吗?1知识点内错角知1-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且分别在第三条直线的
两侧,具有这种位置关系的一对角叫做内错角.
如图,∠1与∠2,∠3与∠4
都是内错角.分别画出∠1
与∠2的两条边,可发现组
成这一对角的“三条线”的图像字母Z.知1-讲要点精析:
(1)内错角是成对出现的,并且是由三条直线组成的,
一边共线另两边不共线;
(2)内错角的顶点不是公共的;
(3)“内”可理解为夹在两直线之间,“错”可理解为
交错,即位于第三条直线的两侧;内错角的位置关
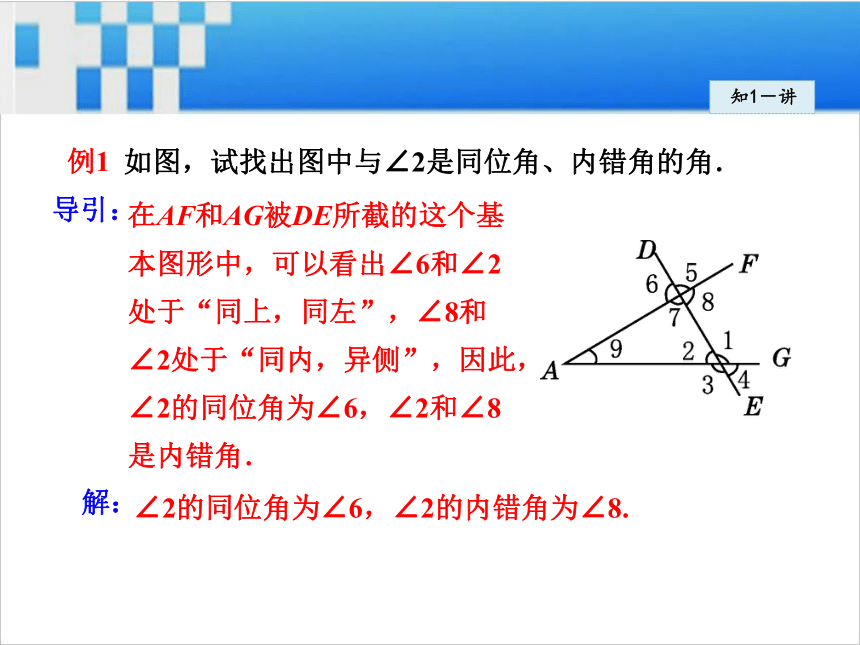
系具有“同内、异侧”的特征.知1-讲例1 如图,试找出图中与∠2是同位角、内错角的角.在AF和AG被DE所截的这个基
本图形中,可以看出∠6和∠2
处于“同上,同左”,∠8和
∠2处于“同内,异侧”,因此,
∠2的同位角为∠6,∠2和∠8
是内错角.导引:∠2的同位角为∠6,∠2的内错角为∠8.解: 寻找一个角的同位角、内错角,首先应该把这
个角放在一个“三线八角”的基本图形中,其次不
管是同位角,还是内错角,它们具有一个共同特征,
这两个角有一边在同一直线上,这条直线就是定义
中的“第三条直线”,而这两个角剩下的两边所在
的直线就是两条被截的直线 ;最后看这两个角的位
置特征是否满足同位角、内错角的位置特征:三边
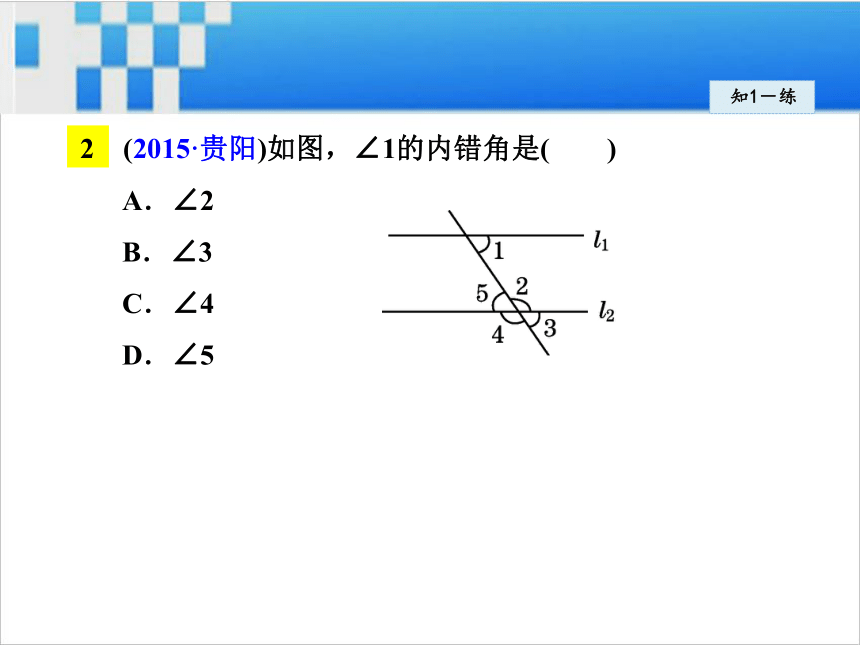
成“F”“Z”形.知1-讲知1-练1 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是__________.知1-练2 (2015·贵阳)如图,∠1的内错角是( )
A.∠2
B.∠3
C.∠4
D.∠5知1-练3 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )2知识点同旁内角 知2-讲1.定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且它们都在第三条直线
的同一旁.具有这种位置关系的一对角叫做同旁内角;
如图中的∠1与∠2,∠3与∠4
都是同旁内角;分别画出它们
的两条边,可发现组成这一对
角的“三条线”的图像字母U. 知2-讲要点精析:
(1)同旁内角是成对出现的,并且是由三条直线组成的,
一边共线,另两边不共线;
(2)同旁内角的顶点不是公共的;
(3)“同旁”即在第三条直线的同一旁,“内”表示为夹
在两直线之间;同旁内角的位置关系具有“同内、同
侧”的特征.知2-讲2.同位角、内错角、同旁内角的特征:知2-讲3.识别同位角、内错角和同旁内角的方法:
(1)定义法:“一看三线、二找截线、三查位置来分辨”;
这三种角的共同特征是:一边共线,不共顶点,两
角的另一边分别在两条直线上;再根据位置关系确
定是哪种角;
(2)分离图形法:区分这三种角的较准确,较快捷的方
法是通过分离图形,把每一对角从图形中分离出来,
观察分离出的这三种角的形状结构特征,找出规律
加以区分;知2-讲(3)粗描相关线条法:把相关的一对角用粗线条描出,
两角关系便极易识别;
(4)特征法:把相关的一对角用彩色描出,看其是否符
合“F”“Z”“U”形特征;
(5)方位法:
同位角:同左、同上,同左、同下,同右、同上,
同右、同下;
内错角:同内、异侧;
同旁内角:同内、同侧.知2-讲例2 如图,下列说法错误的是( )
A.∠C 与∠1 是内错角
B.∠2与∠3是内错角
C.∠A与∠B 是同旁内角
D.∠A与∠3是同位角选项A,C,D 分别符合内错角、同旁内角、同位
角的定义,而∠2 与∠3是一对补角. 导引:B 本题运用定义法. 识别同位角、内错角、同旁内
角的关键是看两个角所涉及直线是否只有三条,并
且有没有一条边在同一直线(截线)上,如果没有,就
不是;如果有,再根据角的位置特征判断.知2-讲知2-讲例3 如图,∠1 与∠2 ,∠ 3 与∠4分别是内错角,它们分别是由哪两条直线被哪一条直线所截得到的?∠1 与∠2 是直线AD 与 BC 被直
线 AC 所截得到的,∠ 3 与∠4
是直线AB 与 DC 被直线BD所截
得到的.
错解中没有分清∠1与∠2,∠3与∠4分别是由
哪两条直线被第三条直线所截得到的,而导致错误.
应根据相关的概念来确定.错解:错解分析:知2-讲 ∠1 与∠2 是直线 AB 与 DC 被直线 AC 所截
得到的,∠ 3 与∠4 是直线 AD 与 BC 被直线 BD 所
截得到的.正确解法解: 三线八角由三条直线构成,其中互为同位角、内
错角、同旁内角的两个角的公共边所在的直线是截线,
两个角的另一边所在的两条直线是被截直线.知2-讲1 如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
A.∠1
B.∠2
C.∠4
D.∠5知2-练2 如图,与∠B是同旁内角的角有( )
A.1个
B.2个
C.3个
D.4个知2-练3知识点内错角相等,两直线平行 知3-导议一议
(1)内错角满足什么关系时,两直线平行?为什么? 两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.
简称为:内错角相等,两直线平行.知3-导知3-讲1.判定方法2:两条直线被第三条直线所截,如果内错
角相等,那么这两条直线平行
简称:内错角相等,两直线平行.
表达方式:
如图:
因为∠1=∠2(已知),
所以a∥b(内错角相等,两直线平行). 知3-讲要点精析:
(1)“内错角相等,两直线平行”.它可利用“同位角相
等,两直线平行”结合“对顶角相等”推导得出;
(2)利用“内错角相等”来确定“两直线平行”的关键
是弄清这对内错角是哪两条直线被第三条直线所截
得到的内错角,再说明这两条直线平行;
(3)说明两直线平行,只需一对内错角相等即可.
2.易错警示:易找错要证明两条直线平行的内错角.知3-讲例4 如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC∠AEF和∠EFC是直线AB,CD被直线EF所截得到
的内错角,根据“内错角相等,两直线平行”可知,
AB∥CD.导引:B利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两条直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,
看其是否相等.若相等,则两条直线平行.知3-讲知3-讲例5 如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试说明:DF∥BE.要想说明DF∥BE,可通
过说明∠1=∠EDF来实
现,由于∠1=30°,所
以只需求出∠EDF=30°,
而这个结论可通过DF是
∠ADE的平分线来求得.导引:知3-讲因为DF平分∠ADE(已知),
所以∠EDF= ∠ADE(角平分线的定义).
又因为∠ADE=60°(已知),
所以∠EDF=30°.
又因为∠1=30°(已知),
所以∠EDF=∠1.
所以DF∥EB(内错角相等,两直线平行).解: 要判定两直线平行可以通过说明同位角相等或内
错角相等来实现,至于到底选用同位角还是选用内错
角,要看具体的题目,要尽可能与已知条件联系.知3-讲1 (中考·汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE知3-练2 (2015·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( )知3-练3 如图,若∠1与∠2互补,∠2与∠4互补,则( )
A.l4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3知3-练4知识点同旁内角互补,两直线平行知4-导议一议
(2)同旁内角满足什么关系时,两直线平行?为什么?? 两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称为:同旁内角互补,两直线平行.知4-导知4-讲判定方法3:两条直线被第三条直线所截,如果同旁内
角互补,那么这两条直线平行;
简称:同旁内角互补,两直线平行.
表达方式:
如图:
因为∠1+∠2=180°(已知),
所以a∥b(同旁内角互补,两直线平行).知4-讲要点精析:
(1)利用同旁内角证明两直线平行时,同旁内角之间的
关系是互补,不是相等.
(2)在“三线八角”中:同位角相等、内错角相等、同
旁内角互补中,只要其中一个结论成立,则利用对
顶角、补角等相关知识,可得到另两个结论也成立.知4-讲例6 如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?由题意可知
∠1=∠AOD=70°,
又因为∠A=110°,
所以∠A+∠AOD=180°,
故AB∥CD.导引:知4-讲因为∠1=∠AOD(对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).解:(1)本题运用数形结合思想.平行线的判定是由角之
间的数量关系到“形”的判定.要判定两直线平
行,可围绕截线找同位角、内错角或同旁内角,
若同位角相等、内错角相等或同旁内角互补,则
两直线平行.
(2)若题中的结论能用同位角相等、内错角相等或同
旁内角互补中的一个方法说明两直线平行时,一
般都要通过结合对顶角、互补角等知识来说明.知4-讲1 (2016·赤峰)如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD相交知4-练2 (2015·黔南州)如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,
则a∥c知4-练3 如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2
B.∠DAB+∠D=180°
C.∠3=∠4
D.∠B=∠DCE知4-练平行线的判定方法:
(1)内错角相等,两直线平行;
(2)同旁内角互补,两直线平行;
旁内角”判定
平行线第二章 相交线与平行线2.2 探索直线平行的条件1课堂讲解内错角
同旁内角
内错角相等,两直线平行
同旁内角互补,两直线平行2课时流程逐点
导讲练课堂小结作业提升 小明有一块小画板(如图),他想知道它的上、下边
缘是否平行,于是他在两个边缘之间画了一条线段AB. 小明身边只有一个量角器,他通过测量某些角的大
小就能知道这个画板的上、下边缘是否平行,你知道他
是怎样做的吗?1知识点内错角知1-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且分别在第三条直线的
两侧,具有这种位置关系的一对角叫做内错角.
如图,∠1与∠2,∠3与∠4
都是内错角.分别画出∠1
与∠2的两条边,可发现组
成这一对角的“三条线”的图像字母Z.知1-讲要点精析:
(1)内错角是成对出现的,并且是由三条直线组成的,
一边共线另两边不共线;
(2)内错角的顶点不是公共的;
(3)“内”可理解为夹在两直线之间,“错”可理解为
交错,即位于第三条直线的两侧;内错角的位置关
系具有“同内、异侧”的特征.知1-讲例1 如图,试找出图中与∠2是同位角、内错角的角.在AF和AG被DE所截的这个基
本图形中,可以看出∠6和∠2
处于“同上,同左”,∠8和
∠2处于“同内,异侧”,因此,
∠2的同位角为∠6,∠2和∠8
是内错角.导引:∠2的同位角为∠6,∠2的内错角为∠8.解: 寻找一个角的同位角、内错角,首先应该把这
个角放在一个“三线八角”的基本图形中,其次不
管是同位角,还是内错角,它们具有一个共同特征,
这两个角有一边在同一直线上,这条直线就是定义
中的“第三条直线”,而这两个角剩下的两边所在
的直线就是两条被截的直线 ;最后看这两个角的位
置特征是否满足同位角、内错角的位置特征:三边
成“F”“Z”形.知1-讲知1-练1 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是__________.知1-练2 (2015·贵阳)如图,∠1的内错角是( )
A.∠2
B.∠3
C.∠4
D.∠5知1-练3 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )2知识点同旁内角 知2-讲1.定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且它们都在第三条直线
的同一旁.具有这种位置关系的一对角叫做同旁内角;
如图中的∠1与∠2,∠3与∠4
都是同旁内角;分别画出它们
的两条边,可发现组成这一对
角的“三条线”的图像字母U. 知2-讲要点精析:
(1)同旁内角是成对出现的,并且是由三条直线组成的,
一边共线,另两边不共线;
(2)同旁内角的顶点不是公共的;
(3)“同旁”即在第三条直线的同一旁,“内”表示为夹
在两直线之间;同旁内角的位置关系具有“同内、同
侧”的特征.知2-讲2.同位角、内错角、同旁内角的特征:知2-讲3.识别同位角、内错角和同旁内角的方法:
(1)定义法:“一看三线、二找截线、三查位置来分辨”;
这三种角的共同特征是:一边共线,不共顶点,两
角的另一边分别在两条直线上;再根据位置关系确
定是哪种角;
(2)分离图形法:区分这三种角的较准确,较快捷的方
法是通过分离图形,把每一对角从图形中分离出来,
观察分离出的这三种角的形状结构特征,找出规律
加以区分;知2-讲(3)粗描相关线条法:把相关的一对角用粗线条描出,
两角关系便极易识别;
(4)特征法:把相关的一对角用彩色描出,看其是否符
合“F”“Z”“U”形特征;
(5)方位法:
同位角:同左、同上,同左、同下,同右、同上,
同右、同下;
内错角:同内、异侧;
同旁内角:同内、同侧.知2-讲例2 如图,下列说法错误的是( )
A.∠C 与∠1 是内错角
B.∠2与∠3是内错角
C.∠A与∠B 是同旁内角
D.∠A与∠3是同位角选项A,C,D 分别符合内错角、同旁内角、同位
角的定义,而∠2 与∠3是一对补角. 导引:B 本题运用定义法. 识别同位角、内错角、同旁内
角的关键是看两个角所涉及直线是否只有三条,并
且有没有一条边在同一直线(截线)上,如果没有,就
不是;如果有,再根据角的位置特征判断.知2-讲知2-讲例3 如图,∠1 与∠2 ,∠ 3 与∠4分别是内错角,它们分别是由哪两条直线被哪一条直线所截得到的?∠1 与∠2 是直线AD 与 BC 被直
线 AC 所截得到的,∠ 3 与∠4
是直线AB 与 DC 被直线BD所截
得到的.
错解中没有分清∠1与∠2,∠3与∠4分别是由
哪两条直线被第三条直线所截得到的,而导致错误.
应根据相关的概念来确定.错解:错解分析:知2-讲 ∠1 与∠2 是直线 AB 与 DC 被直线 AC 所截
得到的,∠ 3 与∠4 是直线 AD 与 BC 被直线 BD 所
截得到的.正确解法解: 三线八角由三条直线构成,其中互为同位角、内
错角、同旁内角的两个角的公共边所在的直线是截线,
两个角的另一边所在的两条直线是被截直线.知2-讲1 如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
A.∠1
B.∠2
C.∠4
D.∠5知2-练2 如图,与∠B是同旁内角的角有( )
A.1个
B.2个
C.3个
D.4个知2-练3知识点内错角相等,两直线平行 知3-导议一议
(1)内错角满足什么关系时,两直线平行?为什么? 两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.
简称为:内错角相等,两直线平行.知3-导知3-讲1.判定方法2:两条直线被第三条直线所截,如果内错
角相等,那么这两条直线平行
简称:内错角相等,两直线平行.
表达方式:
如图:
因为∠1=∠2(已知),
所以a∥b(内错角相等,两直线平行). 知3-讲要点精析:
(1)“内错角相等,两直线平行”.它可利用“同位角相
等,两直线平行”结合“对顶角相等”推导得出;
(2)利用“内错角相等”来确定“两直线平行”的关键
是弄清这对内错角是哪两条直线被第三条直线所截
得到的内错角,再说明这两条直线平行;
(3)说明两直线平行,只需一对内错角相等即可.
2.易错警示:易找错要证明两条直线平行的内错角.知3-讲例4 如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC∠AEF和∠EFC是直线AB,CD被直线EF所截得到
的内错角,根据“内错角相等,两直线平行”可知,
AB∥CD.导引:B利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两条直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,
看其是否相等.若相等,则两条直线平行.知3-讲知3-讲例5 如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试说明:DF∥BE.要想说明DF∥BE,可通
过说明∠1=∠EDF来实
现,由于∠1=30°,所
以只需求出∠EDF=30°,
而这个结论可通过DF是
∠ADE的平分线来求得.导引:知3-讲因为DF平分∠ADE(已知),
所以∠EDF= ∠ADE(角平分线的定义).
又因为∠ADE=60°(已知),
所以∠EDF=30°.
又因为∠1=30°(已知),
所以∠EDF=∠1.
所以DF∥EB(内错角相等,两直线平行).解: 要判定两直线平行可以通过说明同位角相等或内
错角相等来实现,至于到底选用同位角还是选用内错
角,要看具体的题目,要尽可能与已知条件联系.知3-讲1 (中考·汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE知3-练2 (2015·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( )知3-练3 如图,若∠1与∠2互补,∠2与∠4互补,则( )
A.l4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3知3-练4知识点同旁内角互补,两直线平行知4-导议一议
(2)同旁内角满足什么关系时,两直线平行?为什么?? 两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称为:同旁内角互补,两直线平行.知4-导知4-讲判定方法3:两条直线被第三条直线所截,如果同旁内
角互补,那么这两条直线平行;
简称:同旁内角互补,两直线平行.
表达方式:
如图:
因为∠1+∠2=180°(已知),
所以a∥b(同旁内角互补,两直线平行).知4-讲要点精析:
(1)利用同旁内角证明两直线平行时,同旁内角之间的
关系是互补,不是相等.
(2)在“三线八角”中:同位角相等、内错角相等、同
旁内角互补中,只要其中一个结论成立,则利用对
顶角、补角等相关知识,可得到另两个结论也成立.知4-讲例6 如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?由题意可知
∠1=∠AOD=70°,
又因为∠A=110°,
所以∠A+∠AOD=180°,
故AB∥CD.导引:知4-讲因为∠1=∠AOD(对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).解:(1)本题运用数形结合思想.平行线的判定是由角之
间的数量关系到“形”的判定.要判定两直线平
行,可围绕截线找同位角、内错角或同旁内角,
若同位角相等、内错角相等或同旁内角互补,则
两直线平行.
(2)若题中的结论能用同位角相等、内错角相等或同
旁内角互补中的一个方法说明两直线平行时,一
般都要通过结合对顶角、互补角等知识来说明.知4-讲1 (2016·赤峰)如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD相交知4-练2 (2015·黔南州)如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,
则a∥c知4-练3 如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2
B.∠DAB+∠D=180°
C.∠3=∠4
D.∠B=∠DCE知4-练平行线的判定方法:
(1)内错角相等,两直线平行;
(2)同旁内角互补,两直线平行;
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
