4.1.3 三角形的中线、角平分线 课件
文档属性
| 名称 | 4.1.3 三角形的中线、角平分线 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 21:34:29 | ||
图片预览











文档简介
课件30张PPT。第3课时 三角形的中线、
角平分线第四章 三角形4.1 认识三角形1课堂讲解三角形的中线
三角形的重心
三角形的角平分线2课时流程逐点
导讲练课堂小结作业提升1.三角形的内角和是多少度?
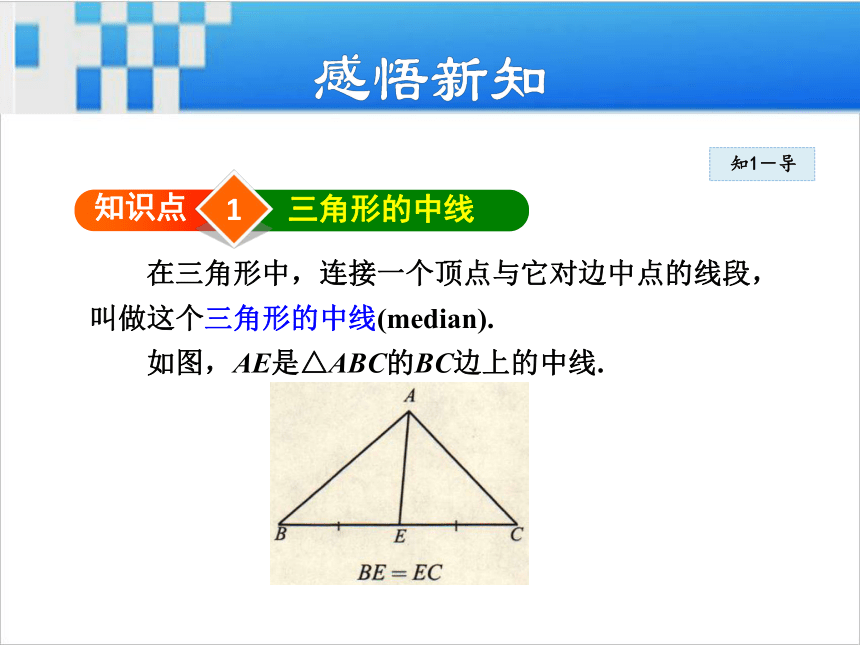
2.三角形的三边关系的内容是什么?复习回顾1知识点三角形的中线知1-导 在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形的中线(median).
如图,AE是△ABC的BC边上的中线.知1-讲1.定义:在三角形中,连接一个顶点与它对边中点的线
段,叫做这个三角形的中线.
2.表达方式:(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC或BD=DC= BC.
注:上述三种情况都表示AD是△ABC的中线,选用哪种
表示法,应根据解题需要合理选用.
3.易错警示:中线是线段,不要将它与线段所在直线混淆.知1-讲例1 〈动手操作题〉在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm的两部分,求三角形的各边长.因为中线BD将△ABC的周长分成两部分:
(BC+CD)和(AD+AB),谁为12 cm,谁为15 cm,
不确定,故应分类讨论;另外题中涉及线段较多,
因此可建立方程模型,利用设未知数来求解.导引:知1-讲设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,
则x+ x=12,解得x=8,
即AB=AC=8 cm,CD=4 cm.
故BC=15-4=11(cm).
此时AB+AC>BC,
所以三边长分别为8 cm,8 cm,11 cm.解:知1-讲(2)如图②,若AB+AD=15 cm,
则x+ x=15,
解得x=10,即AB=AC=10 cm,
则CD=5 cm,
故BC=12-5=7(cm).
显然此时三角形存在,
所以三边长分别为10 cm,10 cm,7 cm.
综上所述,此三角形的三边长分别为8 cm,8 cm,
11 cm或10 cm,10 cm,7 cm.(1)本例中由于条件不确定,因此我们针对条件的不确定性
对图形可能出现的不同情况,运用分类讨论思想对题目
进行分类讨论;解答中,针对题中涉及的线段这个“形”
较多,为了使解答更简便,我们将它们建立方程这个
“数”的模型;因此本例的解答过程体现了:分类讨论
思想、数学建模思想、数形结合思想、方程思想等.
(2)易错警示:求三角形的边时,要注意隐含条件:三角形
的三边关系.知1-讲知1-讲例2 张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.根据等底等高的两个三角形的面
积相等,要等分三角形的面积,
只需要作出一条边上的中线即可.导引:知1-讲根据要求,平分田地的直线只能经过三
角形的顶点.画△ABC的中线AD(如图),
则AD就把△ABC的面积平分成两份.
这是因为AD是△ABC的中线,
所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD
中,因为BD,CD边上的高都是AE,所以由三角形的面
积计算公式,知△ABD和△ACD的面积相等,因此,要
把△ABC平分成两个三角形,只需画中线AD即可,这是
一种平分方法.(本题答案不唯一,作AB,AC边上的中
线也可以)解:(1)三角形的任意一条中线都能把三角形分成面积相等
的两部分,即等底等高的两个三角形的面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.知1-讲知1-练1 若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
2 三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形知1-练3 如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1
C. D.2知识点三角形的重心 知2-导如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?知2-导议一议
(1)在纸上画出一个锐角三角形,并画出它的三条中线,
它们有怎样的位置关系?与同伴进行交流.
(2)钝角三角形和直角三角形的三条中线也有同样的位
置关系吗?折一折,画一画,并与同伴进行交流.铅笔支起三角形卡片的点就是三角形的重心!知2-导知2-讲位置图例:任何三角形的三条中线都交于一点,且该
点在三角形的内部,如图,这个点叫三角形的重心.1 已知三角形的三条中线交于一点,则下列结论:
①这一点在三角形的内部;
②这一点有可能在三角形的外部;
③这一点是三角形的重心.
其中正确的结论有________.(填序号)
2 有一质地均匀的三角形铁片,若阿龙想用木棒撑住此铁片,则支撑点应设在该三角形的________处最恰当.知2-练3知识点三角形的角平分线知3-导 在三角形中,一个内角的角平分线与它的对边相
交,这个角的顶点与交点之间的线段叫做三角形的角
平分线.如图,AD是△ABC的一条角平分线.知3-讲1.定义:在三角形中,一个内角的角平分线与它的对
边相交,这个角的顶点和交点之间的线段叫做三角
形的角平分线.
2.位置图例:任何三角形的三条角平分线交于一点,
且该点在三角形的内部,这个点叫这个三角形的内
心.如图所示.
3.表达方式:
(1)AD是△ABC的角平分线;
(2)AD平分∠BAC交BC于点D;
(3)∠BAD=∠CAD= ∠BAC.知3-讲注:上述三种情况都表示同一意义,即AD是△ABC
的角平分线,选用哪种表示法,应根据解题需要合
理选用.
4.易错警示:角的平分线是一条射线,而三角形的角
平分线是一条线段,不要混淆.知3-讲例3 关于三角形的角平分线,下列说法正确的是( )
A.是线段
B.是射线
C.是直线
D.可以是射线或线段三角形的角平分线是一条线段,故选A.导引:A 三角形的角平分线与角的平分线是不同的两个
概念:三角形的角平分线是一条线段,而角的平分
线是一条射线;一个三角形的角平分线有三条,一
个角的平分线只有一条;在三角形中,三角形的角
平分线是三角形的内角平分线上的一部分.本题易
因混淆概念而错选D.知3-讲知3-讲例4 如图所示,AD是△ABC的角平分线,AE是△ABD的角平分线,∠BAC=80°,则∠EAD的度数是( )
A.20° B.30° C.45° D.60°因为AD平分∠BAC,∠BAC=80°,
所以∠BAD=40°.
又因为AE平分∠BAD,
所以∠EAD=20°.导引:A 三角形的角平分线将三角形的内角分成相等的
两部分,特别是两角之间的数量关系在求角的度数
时起着关键作用.知3-讲1 下列说法中正确的是( )
A.三角形的角平分线和中线都是线段
B.三角形的角平分线和中线都是射线
C.三角形的角平分线是射线,而中线是线段
D.三角形的角平分线是线段,而中线是射线知3-练2 如图,BD平分∠ABC,CD平分∠ACB,若∠A=50°,则∠D等于( )
A.120° B.130°
C.115° D.110°知3-练1.三角形的中线
(1)定义:三角形的中线是一条线段.
(2)三角形的三条中线相交于一点,这一点叫做三角形
的重心.
(3)面积法是一种常用的、重要的数学解题思想方法,
它利用同一图形面积相等、等底等高的三角形面积
相等、三角形中线分三角形为面积相等的两部分、
分割后的各图形面积之和等于原图形的面积等解决
有关数学问题.2.三角形的角平分线
(1)定义:三角形的角平分线是一条线段.
(2)三角形三条角平分线相交于一点,这一点叫做三角
形的内心.
角平分线第四章 三角形4.1 认识三角形1课堂讲解三角形的中线
三角形的重心
三角形的角平分线2课时流程逐点
导讲练课堂小结作业提升1.三角形的内角和是多少度?
2.三角形的三边关系的内容是什么?复习回顾1知识点三角形的中线知1-导 在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形的中线(median).
如图,AE是△ABC的BC边上的中线.知1-讲1.定义:在三角形中,连接一个顶点与它对边中点的线
段,叫做这个三角形的中线.
2.表达方式:(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC或BD=DC= BC.
注:上述三种情况都表示AD是△ABC的中线,选用哪种
表示法,应根据解题需要合理选用.
3.易错警示:中线是线段,不要将它与线段所在直线混淆.知1-讲例1 〈动手操作题〉在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm的两部分,求三角形的各边长.因为中线BD将△ABC的周长分成两部分:
(BC+CD)和(AD+AB),谁为12 cm,谁为15 cm,
不确定,故应分类讨论;另外题中涉及线段较多,
因此可建立方程模型,利用设未知数来求解.导引:知1-讲设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,
则x+ x=12,解得x=8,
即AB=AC=8 cm,CD=4 cm.
故BC=15-4=11(cm).
此时AB+AC>BC,
所以三边长分别为8 cm,8 cm,11 cm.解:知1-讲(2)如图②,若AB+AD=15 cm,
则x+ x=15,
解得x=10,即AB=AC=10 cm,
则CD=5 cm,
故BC=12-5=7(cm).
显然此时三角形存在,
所以三边长分别为10 cm,10 cm,7 cm.
综上所述,此三角形的三边长分别为8 cm,8 cm,
11 cm或10 cm,10 cm,7 cm.(1)本例中由于条件不确定,因此我们针对条件的不确定性
对图形可能出现的不同情况,运用分类讨论思想对题目
进行分类讨论;解答中,针对题中涉及的线段这个“形”
较多,为了使解答更简便,我们将它们建立方程这个
“数”的模型;因此本例的解答过程体现了:分类讨论
思想、数学建模思想、数形结合思想、方程思想等.
(2)易错警示:求三角形的边时,要注意隐含条件:三角形
的三边关系.知1-讲知1-讲例2 张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.根据等底等高的两个三角形的面
积相等,要等分三角形的面积,
只需要作出一条边上的中线即可.导引:知1-讲根据要求,平分田地的直线只能经过三
角形的顶点.画△ABC的中线AD(如图),
则AD就把△ABC的面积平分成两份.
这是因为AD是△ABC的中线,
所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD
中,因为BD,CD边上的高都是AE,所以由三角形的面
积计算公式,知△ABD和△ACD的面积相等,因此,要
把△ABC平分成两个三角形,只需画中线AD即可,这是
一种平分方法.(本题答案不唯一,作AB,AC边上的中
线也可以)解:(1)三角形的任意一条中线都能把三角形分成面积相等
的两部分,即等底等高的两个三角形的面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.知1-讲知1-练1 若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
2 三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形知1-练3 如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1
C. D.2知识点三角形的重心 知2-导如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?知2-导议一议
(1)在纸上画出一个锐角三角形,并画出它的三条中线,
它们有怎样的位置关系?与同伴进行交流.
(2)钝角三角形和直角三角形的三条中线也有同样的位
置关系吗?折一折,画一画,并与同伴进行交流.铅笔支起三角形卡片的点就是三角形的重心!知2-导知2-讲位置图例:任何三角形的三条中线都交于一点,且该
点在三角形的内部,如图,这个点叫三角形的重心.1 已知三角形的三条中线交于一点,则下列结论:
①这一点在三角形的内部;
②这一点有可能在三角形的外部;
③这一点是三角形的重心.
其中正确的结论有________.(填序号)
2 有一质地均匀的三角形铁片,若阿龙想用木棒撑住此铁片,则支撑点应设在该三角形的________处最恰当.知2-练3知识点三角形的角平分线知3-导 在三角形中,一个内角的角平分线与它的对边相
交,这个角的顶点与交点之间的线段叫做三角形的角
平分线.如图,AD是△ABC的一条角平分线.知3-讲1.定义:在三角形中,一个内角的角平分线与它的对
边相交,这个角的顶点和交点之间的线段叫做三角
形的角平分线.
2.位置图例:任何三角形的三条角平分线交于一点,
且该点在三角形的内部,这个点叫这个三角形的内
心.如图所示.
3.表达方式:
(1)AD是△ABC的角平分线;
(2)AD平分∠BAC交BC于点D;
(3)∠BAD=∠CAD= ∠BAC.知3-讲注:上述三种情况都表示同一意义,即AD是△ABC
的角平分线,选用哪种表示法,应根据解题需要合
理选用.
4.易错警示:角的平分线是一条射线,而三角形的角
平分线是一条线段,不要混淆.知3-讲例3 关于三角形的角平分线,下列说法正确的是( )
A.是线段
B.是射线
C.是直线
D.可以是射线或线段三角形的角平分线是一条线段,故选A.导引:A 三角形的角平分线与角的平分线是不同的两个
概念:三角形的角平分线是一条线段,而角的平分
线是一条射线;一个三角形的角平分线有三条,一
个角的平分线只有一条;在三角形中,三角形的角
平分线是三角形的内角平分线上的一部分.本题易
因混淆概念而错选D.知3-讲知3-讲例4 如图所示,AD是△ABC的角平分线,AE是△ABD的角平分线,∠BAC=80°,则∠EAD的度数是( )
A.20° B.30° C.45° D.60°因为AD平分∠BAC,∠BAC=80°,
所以∠BAD=40°.
又因为AE平分∠BAD,
所以∠EAD=20°.导引:A 三角形的角平分线将三角形的内角分成相等的
两部分,特别是两角之间的数量关系在求角的度数
时起着关键作用.知3-讲1 下列说法中正确的是( )
A.三角形的角平分线和中线都是线段
B.三角形的角平分线和中线都是射线
C.三角形的角平分线是射线,而中线是线段
D.三角形的角平分线是线段,而中线是射线知3-练2 如图,BD平分∠ABC,CD平分∠ACB,若∠A=50°,则∠D等于( )
A.120° B.130°
C.115° D.110°知3-练1.三角形的中线
(1)定义:三角形的中线是一条线段.
(2)三角形的三条中线相交于一点,这一点叫做三角形
的重心.
(3)面积法是一种常用的、重要的数学解题思想方法,
它利用同一图形面积相等、等底等高的三角形面积
相等、三角形中线分三角形为面积相等的两部分、
分割后的各图形面积之和等于原图形的面积等解决
有关数学问题.2.三角形的角平分线
(1)定义:三角形的角平分线是一条线段.
(2)三角形三条角平分线相交于一点,这一点叫做三角
形的内心.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
