4.1.4 三角形的高线课件

课件28张PPT。第4课时 三角形的高线第四章 三角形4.1 认识三角形1课堂讲解三角形的高
三角形高的位置2课时流程逐点
导讲练课堂小结作业提升1.什么是三角形的中线？什么是三角形的角平分线？
2.三角形的三条中线、角平分线相交于一点吗？
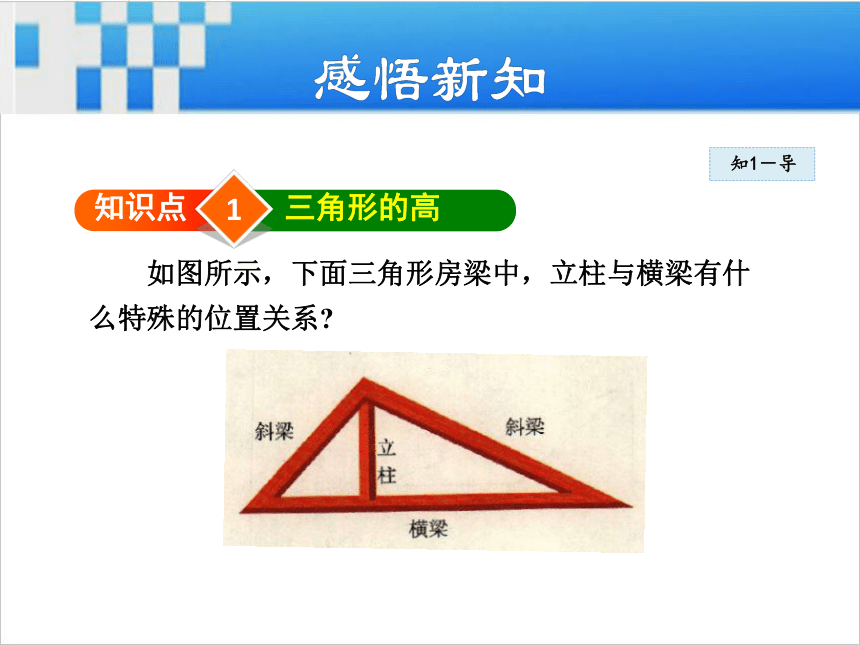
这一交点在三角形的内部还是外部？复习回顾1知识点三角形的高知1－导 如图所示，下面三角形房梁中，立柱与横梁有什
么特殊的位置关系? 从三角形的一个顶点向它的对边所在直线作垂线，
顶点和垂足之间的线段叫做三角形的高线，简称三角
形的高(height).如图，线段AF是△ABC的BC边上的高.知1－导知1－讲1.定义：从三角形的一个顶点向它的对边所在直线作垂
线，顶点和垂足之间的线段叫做三角形的高线，简称
三角形的高；一个三角形有三条高．
3.表达方式：(1)AD是△ABC的BC边上的高；
(2)AD⊥BC于点D；
(3)∠ADC＝90°，∠ADB＝90°，
或∠ADC＝∠ADB＝90°.
注：上述三种情况都表示AD是△ABC的高，选用哪种
表示法，应根据解题需要合理选用．知1－讲例1 〈动手操作题，易错题〉 画出下图中△ABC的三条高．(要标明字母，不写画法)“作一边上的高”，即可看成“过
一点(这边所对角的顶点)作已知直
线(这边所在的直线)的垂线．”按
照“过一点作已知直线的垂线”进
行作图，顶点与垂足之间的线段即为该边上的高；
需注意AB，BC边上的高在三角形的外部，作高时
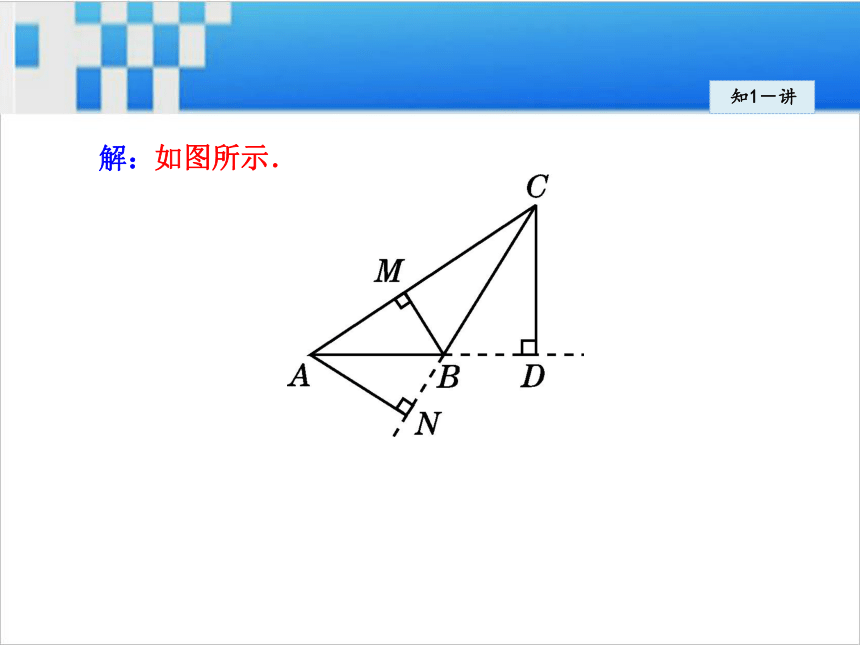
先延长AB与CB.导引：知1－讲如图所示．解：(1)作三角形的高时，找准顶点和对边是关键，作高的
步骤就是“过一点作已知直线的垂线”的步骤：
一靠(三角尺的一条直角边靠在要作高的边上)、
二找(移动三角尺使另一条直角边通过要作高的顶点)、
三画线(画垂线段)，如图.
(2)注意：高是线段，垂线是直线．知1－讲知1－讲例2 〈动手操作题〉如图，在3×2的正方形网格中，小正方形的边长为1，以图中A，B，C，D，E中的三点为顶点的三角形中，面积为1的三角形有哪些？首先要清楚以五点中的三点为顶点
的三角形有多少个，注意C，D，E
三点在一条直线上，不能组成三角
形；再从这些三角形中找出面积为
1的三角形；而要找面积为1的三角
形，根据这些三角形的特征，实质上是要找高为1，
底为2和底为2，高为1的所有三角形．导引：知1－讲以A，B，C，D，E中的三点为顶点的三角形有
△ABC，△ABD，△ABE，△ACD，△ACE，
△ADE，△BCD，△BCE，△BDE.
其中面积为1的有△ABC，△ADE，△BCE，
△ACD.解：(1)三角形的面积与高是密不可分的，只要涉及三角形
的面积就会联想到高，因为三角形的面积等于底与
高乘积的一半；
(2)解答本例的关键是找底和高，注意三角形中大于90°
的角的两边上的高在三角形的外部，这是难点，也
是易错点．知1－讲知1－练1　如图，在△ABC中，BC边上的高是________；在△BCE中，BE边上的高是________；在△ACD中，AC边上的高是________．知1－练2　(2016·淄博)如图，△ABC的面积为16，点D是BC边上一点，且BD＝ BC，点G是AB上一点，点H在△ABC内部，且四边形BDHG是平行四边形，则图中阴影部分的面积是(　　)
A．3　　　　　　
B．4
C．5　　　　
D．62知识点三角形高的位置知2－导做一做
每人准备一个锐角三角形纸片.
(1)你能画出这个三角形的三条高吗？你能用折纸的方
法得到它们吗?
(2)这三条高之间有怎样的位置关系？
将你的结果与同伴进行交流.知2－导议一议
在纸上画出一个直角三角形和一个钝角三角形.
(1)画出直角三角形的三条高，它们有怎样的位置关系?
(2)你能折出钝角三角形的三条高吗？你能画出它们吗??
(3)钝角三角形的三条高交于一点吗？它们所在的直线
交于一点吗? 将你的结果与同伴进行交流.三角形的三条高所在的直线交于一点.知2－导知2－讲1.位置图例：
(1)三个角都是锐角的三角形：三条高都在
三角形的内部，其交点也在三角形的内
部(如图①)；
(2)有一个直角的三角形：一条高在三角形
的内部，其余两条高在三角形边上；其
交点为直角顶点(如图②)；
(3)有一个钝角的三角形：一条高在三角形
的内部，其余两条高在三角形的外部，
其所在直线的交点在三角形的外部(如图
③)．知2－讲2.特别提醒：(1)三角形中的重要线段：三条高、三条中
线、三条角平分线．
(2)三角形中的三个重要的点：三条高的交点叫垂心，
三条中线的交点叫重心，三条角平分线的交点叫内心．
3.易错警示：
(1)三角形中大于90°的角的两边上的高的作法(高均在三
角形的外部)；
(2)任何三角形的三条高所在直线交于一点(垂心)．知2－讲例3 如图，在△ABC中，BC边上的高AD＝4cm，
BC＝4cm，AC＝5cm.
(1)试求△ABC的面积及AC边上的高BE的长；
(2)试求AD∶BE的值．利用三角形面积公式及面
积法求解．导引：知2－讲(1)S△ABC＝ BC·AD＝ ×4×4＝8(cm2)，
因为S△ABC＝ AC·BE＝ ×5×BE＝8(cm2)，
所以BE＝ cm.
(2)AD∶BE＝4∶ ＝ 解： 求三角形的面积联想三角形的高，求三角形的
高联想三角形的面积是解三角形问题中常用的思想
方法之一，而用同一个三角形不同的面积表达式建
立求线段长度的等量关系，是一种很重要的数学方
法：面积法．知2－讲知2－讲例4 如图，已知△ABC中，AB＝AC，DE⊥AB，DF⊥AC，BG⊥AC.试说明：BG＝DE＋DF.要说明线段的和、差关系，需将它
们转化为三角形的高的和、差关系，
再利用面积的和、差关系来解决．
其中只有BG是△ABC的高．
DE，DF要想成为高，很自然地联想
到要连接AD.导引：知2－讲如图，连接AD，因为S△ABC＝S△ABD＋S△ADC，
所以 AC·BG＝ AB·DE＋ AC·DF.
又因为AB＝AC，
所以BG＝DE＋DF.解： “面积法”是数学中很重要的方法，而在涉及垂
直的线段的关系时，常将线段的关系转化为面积的
关系来解决．知2－讲1　如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是(　　)　　　　　　　　　　　
A．锐角三角形 　　　　B．钝角三角形
C．直角三角形 　　　　D．都有可能
2　不一定在三角形内部的线段是(　　)
A．三角形的角平分线 　B．三角形的中线
C．三角形的高 　　　　 D．以上都不对知2－练3　下列结论：
①三角形的角平分线、中线、高都是线段；
②直角三角形只有一条高；
③三角形的中线可能在三角形外部；
④三角形的高都在三角形内部．
其中正确的有(　　)
A．1个　　　 　　　　 B．2个　　　
C．3个　　 　 　　　　 D．4个知2－练1.三角形的高线：
(1)定义；(2)高线的画法；
(3)三角形的三条高线所在的直线相交于一点，这一点
叫做三角形的垂心.
2.特别提醒：(1)三角形中的重要线段：三条高、三条中
线、三条角平分线．
(2)三角形中的三个重要的点：三条高的交点叫垂心，
三条中线的交点叫重心，三条角平分线的交点叫内心．