4.3.3 用“边角边”判定三角形全等 课件
文档属性
| 名称 | 4.3.3 用“边角边”判定三角形全等 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 09:23:44 | ||
图片预览








文档简介
课件29张PPT。第3课时 用“边角边”判定
三角形全等第四章 三角形4.3 探索三角形全等的条件1课堂讲解三角形全等的条件:边角边
全等三角形判定“边角边”的简单应用2课时流程逐点
导讲练课堂小结作业提升 如果已知一个三角形的两边及一角,那么有几种
可能的情况呢?每种情况下得到的三角形都全等吗? 1知识点三角形全等的条件:边角边 知1-导做一做
如果“两边及一角”条件中的角是两边的夹角,比如三
角形两条边分别为2.5cm,3.5cm,它们所夹的角为40°,你
能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
改变上述条件中的角度和边长,再试一试. 两边及其夹角分别相等的两个三角形全等,简写
成“边角边”或 “SAS”.知1-导知1-讲1.判定方法四:两边及其夹角分别相等的两个三角形全
等(简写成“边角边”或“SAS”).
2.书写格式:在△ABC和△A′B′C′中,
因为 所以△ABC≌△A′B′C′(SAS).
要点精析:(1)全等的元素:两边及这两边的夹角;
(2)在书写两个三角形全等的条件边角边时,要按边、
角、边的顺序来写,即把夹角相等写在中间,以突
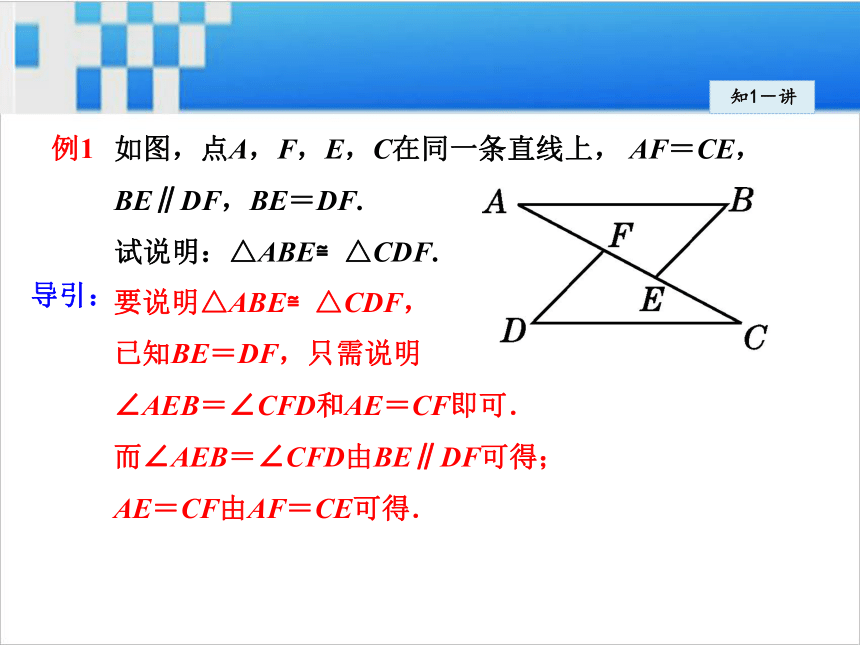
出两边及其夹角对应相等.知1-讲例1 如图,点A,F,E,C在同一条直线上, AF=CE,BE∥DF,BE=DF.
试说明:△ABE≌△CDF.要说明△ABE≌△CDF,
已知BE=DF,只需说明
∠AEB=∠CFD和AE=CF即可.
而∠AEB=∠CFD由BE∥DF可得;
AE=CF由AF=CE可得.导引:知1-讲因为BE∥DF,所以∠AEB=∠CFD.
又因为AF=CE,所以AF+FE=CE+EF,
即AE=CF.
在△ABE和△CDF中,因为
所以△ABE≌△CDF (SAS).解:(1)要判断两个三角形全等,若已知两边相等,可考虑说明
第三边相等或两边的夹角相等,是选用“SSS”还是“SAS”
要根据题目的条件而定,如本题由条件BE∥DF可得角的
关系,故用“SAS”说明.
(2)判断两个三角形全等时,常要说明边相等,而说明边相等
的方法有:①公共边;②等线段加(减)等线段其和(差)相等,
即等式性质;③由中点得到线段相等;④同等于第三条线
段的两线段相等,即等量代换;⑤全等三角形的对应边相
等等.知1-讲知1-讲例2 〈武汉〉如图,AC和BD相交于点O,OA=OC,
OB=OD.试说明:DC∥AB.根据“边角边”可说明
△ODC≌△OBA,
可得∠C=∠A(或者∠D=∠B),
即可说明DC∥AB.导引:知1-讲在△ODC和△OBA中,因为
所以△ODC≌△OBA(SAS).
所以∠C=∠A(或者∠D=∠B)(全等三角形的对应
角相等),
所以DC∥AB(内错角相等,两直线平行).解: 本题可运用分析法寻找说明思路,分析法就是执
果索因,由未知看需知,思维方式上就是从问题入手,
找能求出问题所需要的条件或可行思路,若问题需要
的条件未知,则把所需条件当作中间问题,再找出解
决中间问题的条件.知1-讲知1-练1 如图,a,b,c分别表示△ABC的三边
长,则下面与△ABC一定全等的三角
形是( )知1-练2 (2016·新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能说明△ABC≌△DEF,这个条件是( )
A.∠A=∠D
B.BC=EF
C.∠ACB=∠F
D.AC=DF知1-练3 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;
②AO=CO= AC;
③△ABD≌△CBD,
其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个知1-练4 (2016·永州)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD2知识点全等三角形判定“边角边”的简单应用知2-导议一议
如果“两边及一角”条件中的角是其中一边的对角,
比如两条边分别为2.5cm,3.5cm,长度为2.5 cm的边所对
的角为40°,情况会怎样呢?
小明和小颖按照所给
条件分别画出了图4-31中
的三角形,由此你发现了
什么? 与同伴进行交流. 两边分别相等且其中一组等边的对角相等的两个
三角形不 一定全等.知2-导知2-讲1.易错警示:用两边一角说明三角形全等时,角必须是两边
的夹角.两边和一边的对角分别相等时两个三角形不一定
全等,即不存在“边边角”.
如图,△ABC与△ADC的边
AC=AC,CB=CD,其中
∠A 是CB,CD的对角而非夹角,但△ABC与△ADC不全等.
2.三角形全等的判定方法:在两个三角形的六个元素中(三条
边和三个角),可以判断两个三角形全等的组合有4个:“SSS,
SAS,ASA,AAS”;不能判定两个三角形全等的组合有2个:
“AAA,SSA”.知2-讲例3 〈创新应用题〉如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求
解或推理过程,结果用字母表示).本题让我们了解了测量两点之间距离的一种方法,设计
时,只要需要测量的线段在陆地一侧可实施,就可以达
到目的.导引:知2-讲(1)如图.
(2)在湖岸上找到可以直接到达点A,B
的一点O,连接BO并延长到点C,
使OC=OB;连接AO并延长到点D,
使OD=OA,连接CD,则测量出CD的
长度即为AB的长度.
(3)设CD=m.
因为OD=OA,OC=OB,∠COD=∠BOA,
所以△COD≌△BOA(SAS),
所以CD=AB,即AB=m.解: 解答本题的关键是构造全等三角形,巧妙地借助
两个三角形全等,寻找所求线段与已知线段之间的等
量关系.知2-讲知2-讲例4 如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
试说明:CF=EF.说明CF,EF所在的两个
三角形全等即可.
由Rt△ABC≌Rt△ADE,
可得边角相等关系,进一
步可得△ACD≌△AEB,
进而得出△CDF≌△EBF,
所以可得CF=EF.导引:知2-讲因为Rt△ABC≌Rt△ADE,
所以AC=AE,AB=AD,∠ACB=∠AED,
∠CAB=∠EAD.
所以∠CAB-∠DAB=∠EAD-∠DAB,
即∠DAC=∠BAE.
在△ACD和△AEB中,因为
所以△ACD≌△AEB(SAS).
所以CD=EB,∠ACD=∠AEB.
又因为∠ACB=∠AED,解:知2-讲所以∠ACB-∠ACD=∠AED-∠AEB,
即∠DCF=∠BEF.
在△CDF和△EBF中,因为
所以△CDF≌△EBF(AAS).
所以CF=EF.1 如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm知2-练2 (2016·金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD知2-练3 (中考·云南)如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA.
试说明:AC=BD.知2-练1.应用“SAS”判定两个三角形全等的“两点注意”:
对应:“SAS”包含“边”“角”两种元素,一定要注意元
素的“对应”关系.
顺序:在应用时一定要按边→角→边的顺序排列条件,绝
不能出现边→边→角(或角→边→边)的错误,因为边边角
(或角边边)不能保证两个三角形全等.
2.三角形全等的判定方法:在两个三角形的六个元素中(三条
边和三个角),可以判断两个三角形全等的组合有4个:SSS,
SAS,ASA,AAS”;不能判定两个三角形全等的组合有2个:
“AAA,SSA”.
三角形全等第四章 三角形4.3 探索三角形全等的条件1课堂讲解三角形全等的条件:边角边
全等三角形判定“边角边”的简单应用2课时流程逐点
导讲练课堂小结作业提升 如果已知一个三角形的两边及一角,那么有几种
可能的情况呢?每种情况下得到的三角形都全等吗? 1知识点三角形全等的条件:边角边 知1-导做一做
如果“两边及一角”条件中的角是两边的夹角,比如三
角形两条边分别为2.5cm,3.5cm,它们所夹的角为40°,你
能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
改变上述条件中的角度和边长,再试一试. 两边及其夹角分别相等的两个三角形全等,简写
成“边角边”或 “SAS”.知1-导知1-讲1.判定方法四:两边及其夹角分别相等的两个三角形全
等(简写成“边角边”或“SAS”).
2.书写格式:在△ABC和△A′B′C′中,
因为 所以△ABC≌△A′B′C′(SAS).
要点精析:(1)全等的元素:两边及这两边的夹角;
(2)在书写两个三角形全等的条件边角边时,要按边、
角、边的顺序来写,即把夹角相等写在中间,以突
出两边及其夹角对应相等.知1-讲例1 如图,点A,F,E,C在同一条直线上, AF=CE,BE∥DF,BE=DF.
试说明:△ABE≌△CDF.要说明△ABE≌△CDF,
已知BE=DF,只需说明
∠AEB=∠CFD和AE=CF即可.
而∠AEB=∠CFD由BE∥DF可得;
AE=CF由AF=CE可得.导引:知1-讲因为BE∥DF,所以∠AEB=∠CFD.
又因为AF=CE,所以AF+FE=CE+EF,
即AE=CF.
在△ABE和△CDF中,因为
所以△ABE≌△CDF (SAS).解:(1)要判断两个三角形全等,若已知两边相等,可考虑说明
第三边相等或两边的夹角相等,是选用“SSS”还是“SAS”
要根据题目的条件而定,如本题由条件BE∥DF可得角的
关系,故用“SAS”说明.
(2)判断两个三角形全等时,常要说明边相等,而说明边相等
的方法有:①公共边;②等线段加(减)等线段其和(差)相等,
即等式性质;③由中点得到线段相等;④同等于第三条线
段的两线段相等,即等量代换;⑤全等三角形的对应边相
等等.知1-讲知1-讲例2 〈武汉〉如图,AC和BD相交于点O,OA=OC,
OB=OD.试说明:DC∥AB.根据“边角边”可说明
△ODC≌△OBA,
可得∠C=∠A(或者∠D=∠B),
即可说明DC∥AB.导引:知1-讲在△ODC和△OBA中,因为
所以△ODC≌△OBA(SAS).
所以∠C=∠A(或者∠D=∠B)(全等三角形的对应
角相等),
所以DC∥AB(内错角相等,两直线平行).解: 本题可运用分析法寻找说明思路,分析法就是执
果索因,由未知看需知,思维方式上就是从问题入手,
找能求出问题所需要的条件或可行思路,若问题需要
的条件未知,则把所需条件当作中间问题,再找出解
决中间问题的条件.知1-讲知1-练1 如图,a,b,c分别表示△ABC的三边
长,则下面与△ABC一定全等的三角
形是( )知1-练2 (2016·新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能说明△ABC≌△DEF,这个条件是( )
A.∠A=∠D
B.BC=EF
C.∠ACB=∠F
D.AC=DF知1-练3 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;
②AO=CO= AC;
③△ABD≌△CBD,
其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个知1-练4 (2016·永州)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD2知识点全等三角形判定“边角边”的简单应用知2-导议一议
如果“两边及一角”条件中的角是其中一边的对角,
比如两条边分别为2.5cm,3.5cm,长度为2.5 cm的边所对
的角为40°,情况会怎样呢?
小明和小颖按照所给
条件分别画出了图4-31中
的三角形,由此你发现了
什么? 与同伴进行交流. 两边分别相等且其中一组等边的对角相等的两个
三角形不 一定全等.知2-导知2-讲1.易错警示:用两边一角说明三角形全等时,角必须是两边
的夹角.两边和一边的对角分别相等时两个三角形不一定
全等,即不存在“边边角”.
如图,△ABC与△ADC的边
AC=AC,CB=CD,其中
∠A 是CB,CD的对角而非夹角,但△ABC与△ADC不全等.
2.三角形全等的判定方法:在两个三角形的六个元素中(三条
边和三个角),可以判断两个三角形全等的组合有4个:“SSS,
SAS,ASA,AAS”;不能判定两个三角形全等的组合有2个:
“AAA,SSA”.知2-讲例3 〈创新应用题〉如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求
解或推理过程,结果用字母表示).本题让我们了解了测量两点之间距离的一种方法,设计
时,只要需要测量的线段在陆地一侧可实施,就可以达
到目的.导引:知2-讲(1)如图.
(2)在湖岸上找到可以直接到达点A,B
的一点O,连接BO并延长到点C,
使OC=OB;连接AO并延长到点D,
使OD=OA,连接CD,则测量出CD的
长度即为AB的长度.
(3)设CD=m.
因为OD=OA,OC=OB,∠COD=∠BOA,
所以△COD≌△BOA(SAS),
所以CD=AB,即AB=m.解: 解答本题的关键是构造全等三角形,巧妙地借助
两个三角形全等,寻找所求线段与已知线段之间的等
量关系.知2-讲知2-讲例4 如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
试说明:CF=EF.说明CF,EF所在的两个
三角形全等即可.
由Rt△ABC≌Rt△ADE,
可得边角相等关系,进一
步可得△ACD≌△AEB,
进而得出△CDF≌△EBF,
所以可得CF=EF.导引:知2-讲因为Rt△ABC≌Rt△ADE,
所以AC=AE,AB=AD,∠ACB=∠AED,
∠CAB=∠EAD.
所以∠CAB-∠DAB=∠EAD-∠DAB,
即∠DAC=∠BAE.
在△ACD和△AEB中,因为
所以△ACD≌△AEB(SAS).
所以CD=EB,∠ACD=∠AEB.
又因为∠ACB=∠AED,解:知2-讲所以∠ACB-∠ACD=∠AED-∠AEB,
即∠DCF=∠BEF.
在△CDF和△EBF中,因为
所以△CDF≌△EBF(AAS).
所以CF=EF.1 如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm知2-练2 (2016·金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD知2-练3 (中考·云南)如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA.
试说明:AC=BD.知2-练1.应用“SAS”判定两个三角形全等的“两点注意”:
对应:“SAS”包含“边”“角”两种元素,一定要注意元
素的“对应”关系.
顺序:在应用时一定要按边→角→边的顺序排列条件,绝
不能出现边→边→角(或角→边→边)的错误,因为边边角
(或角边边)不能保证两个三角形全等.
2.三角形全等的判定方法:在两个三角形的六个元素中(三条
边和三个角),可以判断两个三角形全等的组合有4个:SSS,
SAS,ASA,AAS”;不能判定两个三角形全等的组合有2个:
“AAA,SSA”.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
