4.4 用尺规作三角形 课件

课件28张PPT。4.4 用尺规作三角形第四章 三角形1课堂讲解尺规作图
用尺规作三角形2课时流程逐点
导讲练课堂小结作业提升 我们已经会用尺规作一条线段等于已知线段、作
一个角等于已知角，而边和角是三角形的基本元素，
那么你能利用尺规作一个三角形与已知三角形全等吗？1知识点尺规作图知1－讲1.尺规作图的定义：
在几何作图中，把用没有刻度的直尺和圆规作图，简称尺
规作图．
注意：尺规作图指的是只用没有刻度的直尺和圆规两种工具．
2.基本作图：
①作一条线段等于已知线段；②作一个角等于已知角；
③作一个角的平分线；④作线段的垂直平分线；
⑤过一点作已知直线的垂线．知1－练1　基本尺规作图包括：①作一条线段等于________；②作一个角等于________；③作一个角的________；④作一条线段的________；
⑤过一点作已知直线的________．
2　尺规作图的画图工具是(　　)
A．刻度尺、圆规
B．三角板和量角器
C．直尺和量角器
D．没有刻度的直尺和圆规知1－练3　(中考·南通)如图，用尺规作出∠OBF＝∠AOB，作图痕迹 是(　　)
A．以点B为圆心，OD为半径的弧
B．以点B为圆心，DC为半径的弧
C．以点E为圆心，OD为半径的弧
D．以点E为圆心，DC为半径的弧2知识点用尺规作三角形知2－导做一做
1.已知三角形的两边及其夹角，求作这个三角形.
已知：线段a，c，∠α(如图).
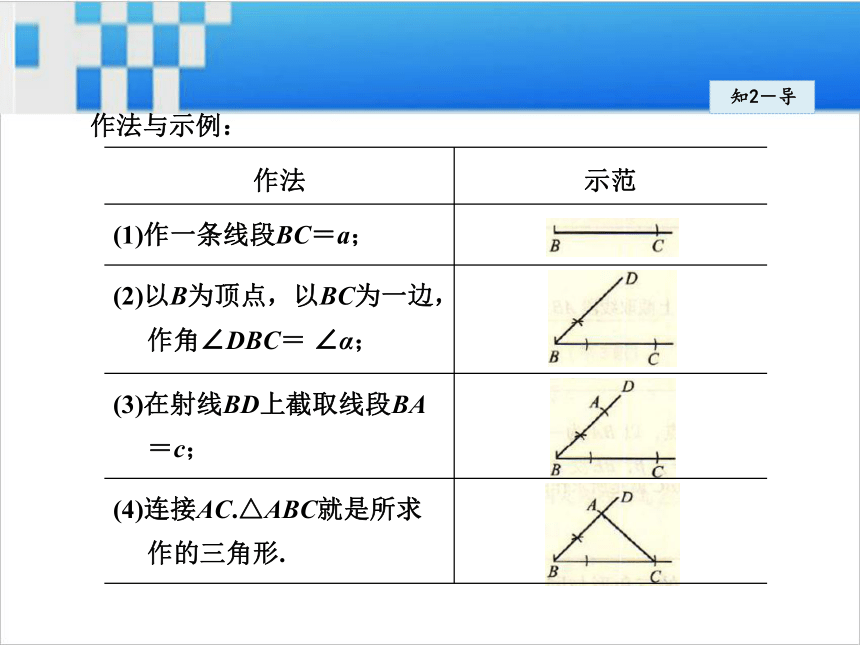
求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.知2－导作法与示例：知2－导2.已知三角形的两角及其夹边，求作这个三角形.
已知：∠α，∠β，线段c(如图).
求作：△ABC，使∠A＝∠α，∠B＝∠β，AB＝c.
请按照给出的作法作出相应的图形.知2－导知2－导3.已知三角形的三条边，求作这个三角形.
已知：线段a，b，c (如图).
求作：△ABC，使AB＝c，AC＝b，BC＝a.
(1)请写出作法并作出相应的图形.
(2)将你所作的三角形与同伴作出的三角形进行比
较，它们全等吗？为什么？知2－讲1.已知两边及其夹角作三角形的依据是SAS；已知两角
及其夹边作三角形的依据是ASA；已知三边作三角形
的依据是SSS.
2.拓展：已知两边，从形状相同，大小相同的角度来看，
所作出的直角三角形是唯一的．
3.要点精析：(1)用尺规作三角形的基本是用尺规作一条
线段等于已知线段和作一个角等于已知角；
(2)用尺规作三角形的依据是三角形全等的判定方法，因
为要使作出的三角形是唯一的，必须使作出的三角形
都是全等的．知2－讲例1 如图所示，已知线段a，c和∠α，求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α，根据作图在下面空格中填上适当的
文字或字母．(1)如图①所示，
作∠MBN＝________；
(2)如图②所示，在射线
BM上截取BC＝_____，
在射线BN上截取 BA＝________；
(3)连接AC，如图③所示，△ABC就是_________________．∠αac所求作的三角形 本题考查学生利用基本作图方法作三角形的能力，
以及准确运用简练的几何语言表达作图方法与步骤的
能力，解题的关键是运用转化思想，将图形语言转化
为几何语言．解答时，也可用尺规按图形中所给的信
息进行操作，进而理解其作法的用意．知2－讲知2－讲例2 如图，已知：∠α，∠β＝90°，线段a.
求作：Rt△ABC，使∠B＝∠α，∠C＝∠β，BC＝2a.
(不写作法，保留作图痕迹)根据题意先画出草图，可
知原题可转化为已知两角
及其夹边，求作三角形的
问题．先画线段BC＝2a，再以B为顶点，BC为一边，
作∠B＝∠α，以C为顶点，BC为一边，在CB的同
侧，作∠C＝∠β，交∠B的另一边于A点．导引：知2－讲如图所示，△ABC即为所求．解： 此题所作三角形的一边长度为已知线段a的2倍，
这一点审题时要稍加注意．此外，此题还可以先作
∠B＝∠α，然后以B为一端点，截取BC＝2a，最后以
C为顶点，CB为一边，在CB的同侧作∠C＝∠β，交
∠B的另一边于A点，这样所成的△ABC也为所求．知2－讲知2－讲例3 如图，已知线段a，b，m，求作△ABC，使BC＝2a，AC＝b，且BC边上的中线AD＝m.解：作法：
(1)作△ADC，使AC＝b，AD＝m，
DC＝a；
(2)作BD＝a；
(3)连接AB，则△ABC即为
所求作的三角形，如图
所示. 本题中，已知，求作已经给出，但该作图题较复
杂，我们可以先进行分析：假设△ABC已经作出，且
满足BC＝2a，AC＝b，BC边上的中线AD＝m，不难发
现△ADC的三边已知，可以先作出△ADC，因为D是
BC的中点，所以在△ADC确定后就可以确定B点的位
置，从而可以作出△ABC，因此我们得出几何作图的
一般步骤：知2－讲知2－讲(1)已知，即将条件具体化；
(2)求作，即具体叙述所作图形应满足的条件；
(3)分析，即寻找作图方法(通常画出草图)；
(4)作法，即根据分析所得的作图方法，作出正式图
形，并依次叙述作图过程；
(5)说明，即验证所作图形的正确性．其中(3)在草稿
纸上进行，(5)通常省略不写．知2－讲例4 如图，△ABC是不等边三角形，DE＝BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，则最多可以作出_______个这样的三角形．4知2－讲导引：如图，以D为圆心，AB长为半径画
弧；以E为圆心，AC长为半径画弧，
两弧相交于两点(DE上、下各一个)，
分别与点D，E连接后，可得到两个
三角形；以D为圆心，AC长为半径
画弧；以E为圆心，AB长为半径画弧，两弧相交于两
点(DE上、下各一个)，分别与点D，E连接后，可得
到两个三角形．因此最多能作出4个符合要求的三角
形． 这是一道探索型题目．解决这类问题的关键是运
用分类讨论思想分析得出所有可能的情况．知2－讲1　利用尺规作三角形，有三种基本类型：
(1)已知三角形的两边及其夹角，求作符合要求的三角形，其作图依据是“________”；
(2)已知三角形的两角及其夹边，求作符合要求的三角形，其作图依据是“________”；
(3)已知三角形的三边，求作符合要求的三角形，其作图依据是“________”．知2－练2　利用基本作图方法，不能作出唯一三角形的是
(　　)
A．已知两边及其夹角
B．已知两角及其夹边
C．已知两边及一边的对角
D．已知三边知2－练3　如图，小敏做试题时，不小心把题目中的三角形用墨水弄污了一部分，她想在一块白纸上作一个完全一样的三角形，然后粘贴在上面，她作图的依据是(　　)
A．SSS 　　　　
B．SAS
C．ASA 　　　　
D．AAS知2－练4　(2016·漳州)下列尺规作图，能判断AD是△ABC边上的高是(　　)知2－练1.尺规作图的定义：
在几何作图中，把用没有刻度的直尺和圆规作图，简称尺
规作图．
注意：尺规作图指的是只用没有刻度的直尺和圆规两种工
具．
2.常见的几种尺规作图：
(1)基本作图：①作一条线段等于已知线段；②作一个角等于
已知角；③作一个角的平分线；④作线段的垂直平分线；
⑤过一点作已知直线的垂线．
(2)作三角形：①已知两边及其夹角作三角形；②已知三边作
三角形；③已知两角及其夹边作三角形．