4.5 利用三角形全等测距离 课件

课件25张PPT。4.5 利用三角形全等
测距离第四章 三角形1课堂讲解利用三角形全等测距离2课时流程逐点
导讲练课堂小结作业提升1.三角形全等的判定方法有哪些？
2.三角形全等的性质有哪些？复习回顾1知识点利用三角形全等测距离知1－导 一位经历过战争的老人讲
述了这样一个故事：
在一次战役中，我军阵地
与敌军碉堡隔河相望.为了炸掉
这个碉堡，需要知道碉堡与我
军阵地的距离.在不能过河测量
又没有任何测量工具的情况下，一个战士想出来这样知1－导一个办法：他面向碉堡的方向站好，然后调整帽子，使
视线通过帽檐正好落在碉堡的底部；然后，他转过一个
角度，保持刚才的姿态，这时视线落在了自己所在岸的
某一点上；接着，他用步测的办法量出自己与那个点的
距离，这个距离就是他与碉堡间的距离.
(1)按这个战士的方法，找出教室或操场上与你距离相等
的两个点，并通过测量加以验证.
(2)你能解释其中的道理吗？知1－导想一想
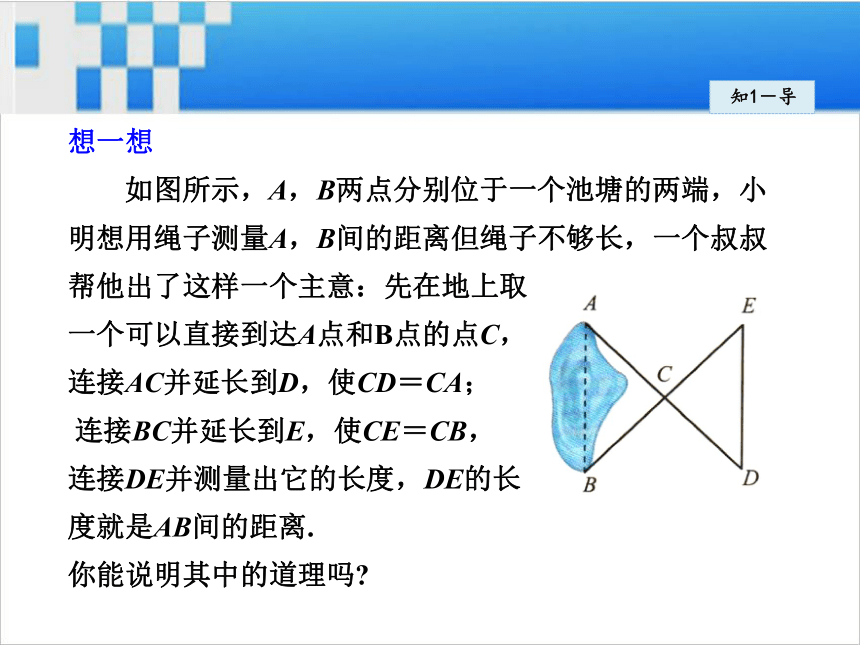
如图所示，A，B两点分别位于一个池塘的两端，小
明想用绳子测量A，B间的距离但绳子不够长，一个叔叔
帮他出了这样一个主意：先在地上取
一个可以直接到达A点和B点的点C，
连接AC并延长到D，使CD＝CA；
连接BC并延长到E，使CE＝CB，
连接DE并测量出它的长度，DE的长
度就是AB间的距离.
你能说明其中的道理吗? 知1－导小明是这样想的：
在△ABC和△DEC中，
因为AC＝DC，∠ACB＝∠DCE，BC＝EC
所以△ABC≌△DEC，
所以AB＝DE.
你能说出每步的道理吗?知1－讲1.当两点之间可以直接到达时，可以直接测量出两点之
间的距离；当两点之间不能直接到达时，可以构造
全等三角形，将不能到达的两点转化到能够到达的
两点来进行测量．
2.通过构造全等三角形来进行测量有以下几种方法：构
造两边和它们的夹角对应相等的两个全等三角形；
构造两角和它们的夹边对应相等的两个全等三角形；
构造三边对应相等的两个全等三角形.知1－讲例1 把两根钢条AB′，BA′的中点连在一起，可以做成一个测量工件内槽宽的工具(卡钳)，如图，若测得A、B间的距离为5厘米，则槽宽为________厘米．如图，连接AB，根据O为AB′和BA′
的中点，可得OA＝OB′，OB＝OA′，
且∠A′OB′＝∠AOB，所以根据
“SAS”即可判定△OA′B′≌△OBA，
所以，测出AB的长度即可求得A′B′
的长度．导引：5 此题中，A′B′的长度无法直接测量，所以构建全
等三角形，通过测量AB的长度来得到A′B′的长度．解
答此题的关键就是构建全等三角形，并确定所要测量
的边的对应边．知1－讲知1－讲例2 如图，在一条河的两岸各耸立着一座宝塔A，B，隔河相对，在无任何过河工具的情况下，你能测量出两座宝塔间的距离吗？说说你的方法和理由．因为没有过河的工具，
所以无法直接测量两塔
间的距离，所以，可通
过构建全等三角形，转
化到岸上来测量．导引：知1－讲能．如图，沿河岸作射线BF，且使
BF⊥AB，在BF上截取BC＝CD，过
D点作DE⊥BF，使点E，C，A在同
一条直线上，则DE的长就是两座宝
塔A、B间的距离．
理由如下：因为在△ACB和△ECD中，

所以△ACB≌△ECD，所以AB＝DE.解： 利用三角形全等来设计测量方案：首先根据已有的条
件和欲测量的问题进行分析，明确要运用哪种方法来构建
全等三角形，即将要用到哪种全等的判定方法；然后，在
测量方案中把说明两个三角形全等所需要的条件毫无遗漏
地“测量到位”．在此题中，首先明确用“ASA”来说明两
个三角形全等，于是在测量方案中设计BF⊥AB，BC＝CD，
DE⊥BF等条件，其目的是要得到利用“ASA”判定三角形
全等所需要的条件．知1－讲知1－讲例3 工人师傅常用角尺平分一个任意角，作法如下：
如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON.移动角尺，使角尺两边相同的刻度分别与M，N重合．则过角尺顶点P的射线OP便是∠AOB的平分线，请你说明理由．导引：易知OM＝ON，OP为公共边，另
外，当角尺两边相同的刻度分别
与M，N重合时，则说明NP＝MP，
所以，可得△MOP≌△NOP，然后根据全等三角形
的性质即可求解．知1－讲解：因为OM＝ON，PM＝PN，OP＝OP，
所以△MOP≌△NOP(SSS)，
所以∠MOP＝∠NOP，
所以OP平分∠MON，
即OP是∠AOB的平分线． 利用三角形全等，不仅可以测量距离，还可以解
决角度、面积、周长等相关问题．解答此题时要善于
运用转化思想与建模思想，将实际问题转化为数学问
题．解答此题的关键是从问题情境中得到两个三角形
全等的条件，如：从“使角尺两边相同的刻度分别与
M，N重合”这一描述性语言中得到NP＝MP.知1－讲知1－讲例4 如图所示是约为两层楼高的人字形钢梁，工人师傅
要检查钢梁的∠B和∠C是否相等，但他手边没有量角器，只有一个长度不到1米的刻度尺．请你帮他设计一个测量方案，并说明理由．导引：分别构建以∠B和∠C为对应角
的两个三角形，然后分别测量两
个三角形的边长，若三组边分别
相等，则两个三角形全等，再通
过全等三角形的性质来判断∠B
和∠C是否相等．知1－讲解：如图，
①分别在BA和CA上量取BE＝CG；
②在BC上量取BD＝CF；
③然后测量出DE与FG的长度，若
DE＝FG，则说明∠B和∠C是相等的．
理由：因为在△BDE和△CFG中，
所以△BDE≌△CFG(SSS)，
所以∠B＝∠C. 设计测量方案的问题往往具有开放性，需要根据
已有条件，围绕测量的问题展开想象，而通过构建全
等三角形来进行测量是常用的方法之一．本题的解答，
正是通过长度的测量构建了△BDE与△CFG这两个全
等三角形，然后利用全等三角形的性质来说明，从而
完成用“刻度尺测量角度”的任务．这一测量过程，
也是建模思想与转化思想的应用．知1－讲1　如图，将两根钢条AA′，BB′的中点O连在一起，使AA′，BB′可以绕着点O自由转动，就做成了一个测量工件，由三角形全等得出A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是
(　　)
A．边角边
B．角边角
C．边边边
D．角角边知1－练2　如图，要测量河中礁石A离岸边B点的距离，采取的方法如下：顺着河岸的方向任作一条线段BC，作∠CBA′＝∠CBA，∠BCA′＝∠BCA.可得△A′BC≌△ABC，所以A′B＝AB，所以测量A′B的长即可得AB的长．判定图中两个三角形全等的理由是(　　)
A．SAS
B．ASA
C．SSS
D．AAS知1－练3　某大学计划为新生配备如图①所示的折叠凳．图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中点．为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30 cm，则由以上信息可推得CB的长度也为30 cm，依据是(　　)
A．SAS
B．ASA
C．SSS
D．AAS知1－练4　(2015·绍兴)如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠PAE.则说明这两个三角形全等的依据是(　　)
A．SAS
B．ASA
C．AAS
D．SSS知1－练5　如图，由两根钢丝固定的高压电线杆，按要求当两根钢丝与电线杆的夹角相同时，固定效果最好．现已知钢丝触地点到电线杆的距离相等，那么请你判断图中两根钢丝的固定是否合乎要求，并说明理由．(电线杆的粗细忽略不计)知1－练1.当两点间的距离难以测量或无法直接测量时，就可以想
办法构造两个全等三角形，利用全等三角形的性质把难
以测量或无法直接测量的距离转化为容易测量的距离．
2.构造全等三角形的依据有：SAS，ASA，AAS，SSS.
3.利用三角形全等解决实际问题的步骤：
(1)明确应用哪些知识来解决实际问题；
(2)根据实际问题抽象出几何图形；
(3)结合图形和题意分析已知条件；
(4)找到已知与未知的联系，寻求恰当的解决途径，并表述
清楚．