6.2.1 频率的稳定性 课件

课件26张PPT。第1课时 频率的稳定性第六章 概率初步6.2 频率的稳定性1课堂讲解频率
频率的稳定性2课时流程逐点
导讲练课堂小结作业提升掷一枚图钉，落地后会出现两种情况：

你认为钉尖朝上和钉尖朝下的可能性一样大吗?1知识点频率 知1－导知1－导(1)两人一组做20次掷图钉的游戏，并将数据记录在下
表中:知1－讲定义：在n次重复试验中，不确定事件A发生了m次，
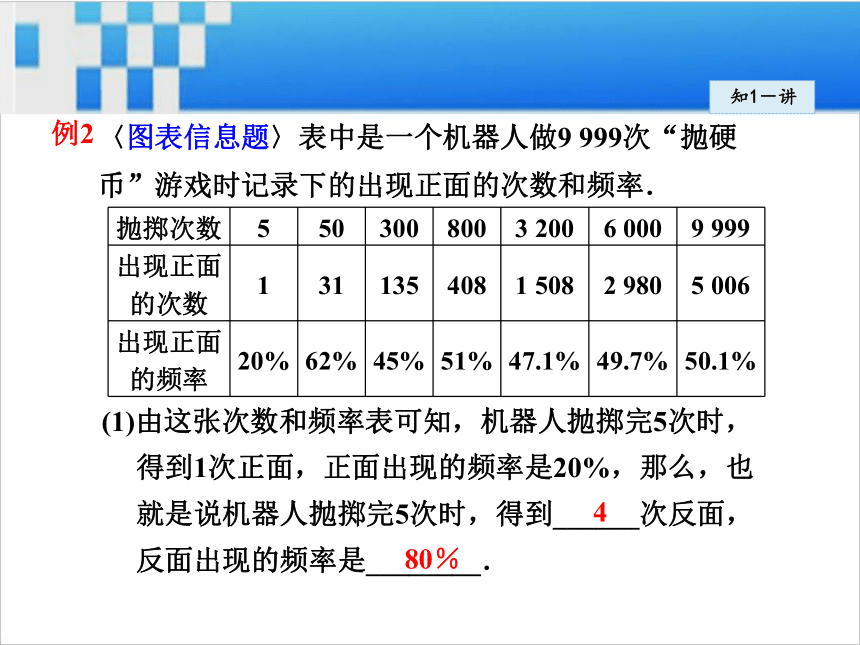
则比值 称为事件 A发生的频率.知1－讲例1 〈长沙〉在一个不透明的盒子中装有n个小球，它们只有颜色上的区别，其中有2个红球，每次摸球前先将盒子中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后发现，摸到红球的频率稳定于0.2，那么可以推算出n大约是________．10知1－讲例2 〈图表信息题〉表中是一个机器人做9 999次“抛硬币”游戏时记录下的出现正面的次数和频率．(1)由这张次数和频率表可知，机器人抛掷完5次时，
得到1次正面，正面出现的频率是20%，那么，也
就是说机器人抛掷完5次时，得到______次反面，
反面出现的频率是________．480％知1－讲(2)由这张次数和频率表可知，机器人抛掷完9 999次时，
得到________次正面，正面出现的频率约是_______．
那么，也就是说机器人抛掷完9 999次时，得到_____
次反面，反面出现的频率约是________．50.1%50064 99349.9%知1－讲利用表中给出的数据进行分析、计算．
(1)抛掷5次，正面次数为1，那么反面次数就是4，
出现反面的频率为 ＝80%，
也可以用1－20%＝80%计算．
(2)抛掷完9 999次，得到5 006次正面，
正面出现的频率约为50.1%，
得到反面就是9 999－5 006＝4 993(次)，
反面出现的频率约为1－50.1%＝49.9%.导引：知1－练1　小胡将一枚质地均匀的硬币抛掷了10次，正面朝上的情况出现了6次，若用A表示正面朝上这一事件，则事件A发生的(　　)
A．频率是0.4
B．频率是0.6
C．频率是6
D．频率接近0.6知1－练2　(2015·苏州)小明统计了他家今年5月份打电话的次数及通话时间，并列出了如下的频数分布表：
则通话时间不超过15 min的频率为(　　)　　　　　　　　　　　　　　　　　　
A．0.1 B．0.4
C．0.5 D．0.92知识点频率的稳定性知2－导(1)累计全班同学的试验结果，并将试验数据汇总填入
下表:知2－导(2)根据上表，完成图6-1的折线统计图:(3)观察图6-1的折线统计图，钉尖朝上的频率的变化
有什么规律？ 在试验次数很大时，钉尖朝上的频率，都会在一
个常数附近摆动，即钉尖朝上的频率具有稳定性.知2－导知2－讲要点精析：
(1)在大量重复试验的情况下，事件的频率会呈现稳定
性，即频率在一个“常数”附近摆动．随着试验次
数的增加，摆动的幅度将越来越小．
(2)频率是一个比值， 没有单位．
(3)频率在一定程度上可以反映随机事件的可能性的大
小，但频率本身是随机的，在试验前不能确定．知2－讲例3 在对某次试验数据整理过程中，某个事件出现的频率随试验次数变化的折线图如图，这个图中折线变化的特点是________，试举一个大致符合这个特点的某事件试验的例子(指出关注的结果)________．知2－讲随着试验次数的增多，频率逐渐稳定在50%；
在掷硬币的试验当中，正面向上的频率有何变
化？(答案不唯一)答案： 随机事件发生的频率具有稳定性，试验次数越多，
稳定性越明显，频率就越接近于一个常数．知2－讲知2－讲例4研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球．怎样估算不同颜色球的数量？
操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球试验．摸球试验的要求：先搅拌均匀，每次随机摸出一个球，放回盒中，再继续．
活动结果：摸球试验一共做了50次，统计结果如下表：
推测计算．由上述的摸球试验可推算：
(1)盒中红球、黄球各占总球数的百分比是多少？
(2)盒中有红球多少个？知2－讲(1)由题意可知，50次摸球试验中，出现红球20次，
黄球30次，
所以红球占总球数的百分比约为20÷50＝40%，
黄球占总球数的百分比约为30÷50＝60%.
所以红球约占40%，黄球约占60%.
(2)由题意可知，50次摸球试验中，出现有记号的球
4次，所以总球数约有8÷ ＝100(个)．
所以红球约有100×40%＝40(个)．解：1　(2016·贵阳)现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽．通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________．知2－练2　某人在做掷硬币试验时，投掷m次，正面朝上有n次(即正面朝上的频率是P＝ ).则下列说法中正确的是(　　)
A．P一定等于
B．P一定不等于
C．多投一次，P更接近
D．随投掷次数逐渐增加，P在 附近摆动知2－练3　在一个不透明的盒子里装着若干个白球，小明想估计其中的白球数，于是他放入10个黑球，搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，得到如下数据：
估计盒子里白球的个数为(　　)
A．8　 　B．40　 　C．80　 　D．无法估计知2－练4　甲、乙两名同学在一次大量重复试验中，统计了某一结果出现的频率，绘制出的统计图如图所示，符合这一结果的试验可能是(　　)
A．掷一枚质地均匀的骰子，
出现1点朝上的频率
B．任意写一个正整数，它
能被3整除的频率
C．抛一枚硬币，出现正面朝上的频率
D．从一个装有2个白球和1个红球的袋子中任取一球，取到白球的频率知2－练1.频率的定义：在n次重复试验中，不确定事件A发生
了m次，则比值 称为事件 A发生的频率.
2.频率的稳定性：
(1)在大量重复试验的情况下，事件的频率会呈现稳定
性，即频率在一个“常数”附近摆动．随着试验次
数的增加，摆动的幅度将越来越小．
(2)频率是一个比值， 没有单位．