1.3.2 零指数幂与负整数指数幂课件
文档属性
| 名称 | 1.3.2 零指数幂与负整数指数幂课件 |  | |
| 格式 | zip | ||
| 文件大小 | 337.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:27:35 | ||
图片预览








文档简介
课件29张PPT。1.3 同底数幂的除法1.3.2 零指数幂与负整
数指数幂第一章 整式的乘除零指数幂
负整数指数幂
整数指数幂的性质逐点
导讲练课堂小结作业提升复习回顾
同底数幂的除法法则是什么?1知识点零指数幂同底数幂相除,如果被除式的指数等于除式的指数,
例如am÷ am ,根据除法的意义可知所得的商为 1 .
另一方面,如果依照同底数幂的除法来计算,又有
am÷ am = am-m = a0 . 知1-导于是规定: a0 =1
这就是说,任何不等于0的数的0次幂都等于1.知1-导1. 零指数幂:任何不等于0的数的0次幂都等于1,
即a0=1(a≠0).
要点精析:(1) 零指数幂在同底数幂除法中,是除式
与被除式的指数相同时的特殊情况.
(2)指数为0,但底数不能为0,因为底数为0,除法无
意义.
拓展:零指数幂中的底数可以是一个不为0的数,也可
以是一个不为0的单项式或多项式.
2. 易错警示:指数为0时忽视底数不为0的条件,即00
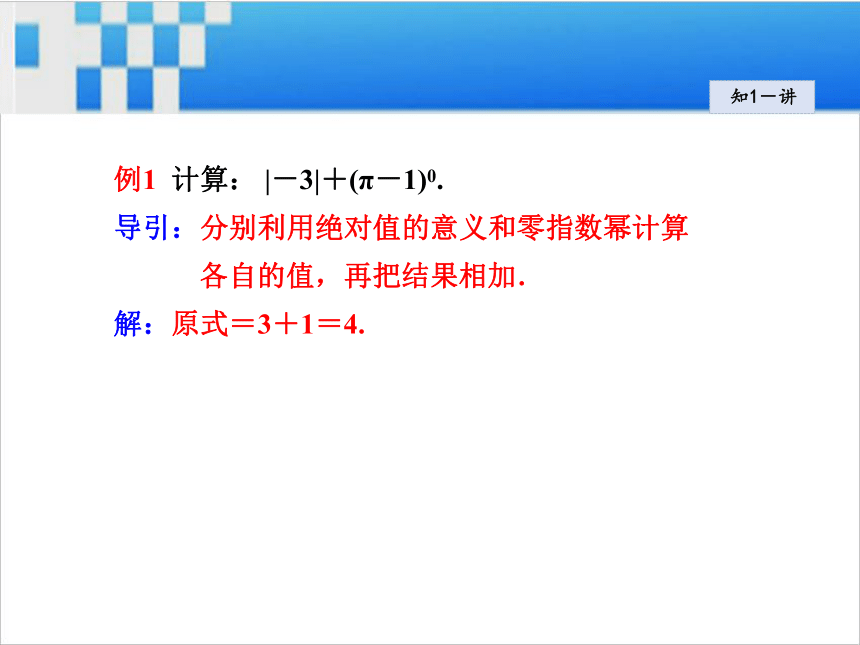
没有意义.知1-讲知1-讲例1 计算: |-3|+(π-1)0.
导引:分别利用绝对值的意义和零指数幂计算
各自的值,再把结果相加.
解:原式=3+1=4.
根据绝对值的意义、0指数幂的意义,先去掉绝对值
符号并完成幂的运算,再做加法运算.知1-讲知1-讲例2 若(x-1)0=1,则x的取值范围是( )
A.x>1 B.x≥1
C.x≤1 D.x≠1
导引:按由零指数幂底数不为0确定x的范围.
由题意得x-1≠0,因此x≠1,故选D.D此题需考虑零指数幂底数不为0.知1-讲知1-讲例3 已知(x-5)x=1,试探究x的可能取值.
错解:当指数为0,即x=0时,(x-5)x=(0-5)0=1.
因此,x的可能取值为0.
错解分析:应按指数为0和底数为1或-1三种情况求
解,错解漏掉两种情况.
正确解法:分三种情况:
(1)当指数为0,即x=0时,(x-5)x=(0-5)0=1;
(2)当底数x-5=1,即x=6时,(x-5)x=(6-5)6=1;
(3)当底数x-5=-1,即x=4时,(x-5)x=(4-5)4=1.
因此,x的可能取值为0,6,4.本题运用分类讨论思想解题.本题的解法紧扣幂为1
时,底数为±1,指数为0的三种情况进行分类,不要
只注意到指数为0的情形,而忽视底数为1或-1的情
形产生漏解.知1-讲知1-练1 (π-x)0=1成立的条件是________.
2 (2016·泰安)计算(-2)0+9÷(-3)的结果是( )
A.-1 B.-2 C.-3 D.-4
3 下列计算正确的是( )
A. =1 B.(-2)0=-1
C.-30=-1 D.(-1)0=02知识点负整数指数幂知2-导猜一猜,下面的括号内该填入什么数?你是怎么想的?
与同伴进行交流.104 =10 000 , 10 ( ) =1 000,
10 ( ) =100 , 10 ( ) =10.24 =16 , 2 ( ) =8,
2 ( ) =4 , 2 ( ) =2.10 ( ) = 1 , 10 ( ) = ,
10 ( ) = , 10 ( ) = .2 ( ) =1 , 2 ( ) = ,
2 ( ) = , 2 ( ) = .知2-讲负整数指数幂法则:
任何不等于零的数的-p( p为正整数)次幂,等于这个
数的p次幂的倒数.
用式子表示为:a-p= (a≠0,p是正整数).
要点精析:
a-p与ap互为倒数,即a-p·ap=1.例4 用小数或分数表示下列各数:
(1) 10-3;(2) 70 ×8-2 ;(3) 1.6×10-4 .
解:知2-讲知2-讲例5 计算:
导引:先分别按照零指数幂法则、正整数指数幂法
则、负整数指数幂法则、绝对值的意义计算,
再进行加减.
解:原式=1-8-3+2=-8.对于底数是分数的负整数指数幂,我们可以将其转化
为这个数的倒数的正整数指数幂,即 .如
本例中 =3,这样就大大地简化了计算.知2-练1 (2015·厦门)2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
2 (中考·泰安)(-2)-2等于( )
A.-4 B.4 C.- D.
3 若(x-3)0-2(3x-6)-2有意义,则x的取值范围
是( )
A.x>3 B.x≠3且x≠2 C.x≠3或x≠2 D.x<23知识点整数指数幂的性质知3-导计算下列各式,你有什么发现?与同伴进行交流.
(1) 7-3÷ 7-5 ;
(2) 3-1÷ 36 ;
(3)
(4) (-8)0÷ (-8)-2 .
只要m,n都是整数,就有am ÷an=am-n成立!知2-练知3-讲在引进了零指数幂和负整数指数幂后,指数的范围已
经扩充到了全体整数,幂的运算性质仍然成立.即有:
(1)am·an=am+n;(2)(am)n=amn;(3)(ab)n=anbn;
(4)am÷an=am-n;(5) ;(6)a0=1.
(这里m,n为整数,a≠0,b≠0)
要点精析:(1)在幂的混合运算中,先计算乘方,再计
算乘除,最后计算加减.
(2)最后结果要化成正整数指数幂.
(3)a-p= 可变形为:a-p·ap=1或 =ap.知2-练知3-讲例6 计算:x2·x3÷x-4=________.
导引:x2·x3÷x-4=x2+3-(-4)=x9.x9运用同底数幂的乘除法法则进行计算,熟记法则并且
正确应用法则是解题的关键.知2-练知3-讲知2-练知3-讲例7 已知10m=3,10n=2,试求102m-n的值.
导引:逆用幂的乘方及同底数幂的除法法则,
进行运算即可.
解: 102m-n=(10m)2÷10n=9÷2=4.5 .
本题应用逆向思维法和代入法解答.先逆用同底数
幂的除法法则和幂的乘方,将所求代数式转化为关
于10m和10n的式子,再将10m和10n的值代入计算.知3-练1 (2016·潍坊)计算:20·2-3=( )
A.- B. C.0 D.8
2 (2015·河北)下列运算正确的是( )
A. B.6×107=6 000 000
C.(2a)2=2a2 D.a3·a2=a5
3 若下列运算正确的是( )
A.a6÷a2=a3 B.(ab2)2=ab4
C.2-3=-6 D.知3-练4 下列各式的计算中,不正确的个数是( )
①100÷10-1=10;
②10-4×(2×7)0=1 000;
③(-0.1)0÷(-2-1)-3=8;
④(-10)-4÷(-10-1)-4=-1.
A.4 B.3 C.2 D.1知3-练5 将 ,(-2)0,(-3)2这三个数按从小到大的顺序排列,正确的是( )
A.(-2)0< <(-3)2
B. <(-2)0<(-3)2
C.(-3)2<(-2)0<
D.(-2)0<(-3)2<1. 零指数幂:
任何不等于0的数的0次幂都等于1,即(a≠0).
2. 负整数指数幂:
(1)负整数指数幂的变形:a-n=
(a≠0,n是正整数).
(2)底数为正数的任何次幂都为正数;底数为负数的
奇次幂是负数,偶次幂是正数.
(3)运算结果要化为正整数指数幂.
数指数幂第一章 整式的乘除零指数幂
负整数指数幂
整数指数幂的性质逐点
导讲练课堂小结作业提升复习回顾
同底数幂的除法法则是什么?1知识点零指数幂同底数幂相除,如果被除式的指数等于除式的指数,
例如am÷ am ,根据除法的意义可知所得的商为 1 .
另一方面,如果依照同底数幂的除法来计算,又有
am÷ am = am-m = a0 . 知1-导于是规定: a0 =1
这就是说,任何不等于0的数的0次幂都等于1.知1-导1. 零指数幂:任何不等于0的数的0次幂都等于1,
即a0=1(a≠0).
要点精析:(1) 零指数幂在同底数幂除法中,是除式
与被除式的指数相同时的特殊情况.
(2)指数为0,但底数不能为0,因为底数为0,除法无
意义.
拓展:零指数幂中的底数可以是一个不为0的数,也可
以是一个不为0的单项式或多项式.
2. 易错警示:指数为0时忽视底数不为0的条件,即00
没有意义.知1-讲知1-讲例1 计算: |-3|+(π-1)0.
导引:分别利用绝对值的意义和零指数幂计算
各自的值,再把结果相加.
解:原式=3+1=4.
根据绝对值的意义、0指数幂的意义,先去掉绝对值
符号并完成幂的运算,再做加法运算.知1-讲知1-讲例2 若(x-1)0=1,则x的取值范围是( )
A.x>1 B.x≥1
C.x≤1 D.x≠1
导引:按由零指数幂底数不为0确定x的范围.
由题意得x-1≠0,因此x≠1,故选D.D此题需考虑零指数幂底数不为0.知1-讲知1-讲例3 已知(x-5)x=1,试探究x的可能取值.
错解:当指数为0,即x=0时,(x-5)x=(0-5)0=1.
因此,x的可能取值为0.
错解分析:应按指数为0和底数为1或-1三种情况求
解,错解漏掉两种情况.
正确解法:分三种情况:
(1)当指数为0,即x=0时,(x-5)x=(0-5)0=1;
(2)当底数x-5=1,即x=6时,(x-5)x=(6-5)6=1;
(3)当底数x-5=-1,即x=4时,(x-5)x=(4-5)4=1.
因此,x的可能取值为0,6,4.本题运用分类讨论思想解题.本题的解法紧扣幂为1
时,底数为±1,指数为0的三种情况进行分类,不要
只注意到指数为0的情形,而忽视底数为1或-1的情
形产生漏解.知1-讲知1-练1 (π-x)0=1成立的条件是________.
2 (2016·泰安)计算(-2)0+9÷(-3)的结果是( )
A.-1 B.-2 C.-3 D.-4
3 下列计算正确的是( )
A. =1 B.(-2)0=-1
C.-30=-1 D.(-1)0=02知识点负整数指数幂知2-导猜一猜,下面的括号内该填入什么数?你是怎么想的?
与同伴进行交流.104 =10 000 , 10 ( ) =1 000,
10 ( ) =100 , 10 ( ) =10.24 =16 , 2 ( ) =8,
2 ( ) =4 , 2 ( ) =2.10 ( ) = 1 , 10 ( ) = ,
10 ( ) = , 10 ( ) = .2 ( ) =1 , 2 ( ) = ,
2 ( ) = , 2 ( ) = .知2-讲负整数指数幂法则:
任何不等于零的数的-p( p为正整数)次幂,等于这个
数的p次幂的倒数.
用式子表示为:a-p= (a≠0,p是正整数).
要点精析:
a-p与ap互为倒数,即a-p·ap=1.例4 用小数或分数表示下列各数:
(1) 10-3;(2) 70 ×8-2 ;(3) 1.6×10-4 .
解:知2-讲知2-讲例5 计算:
导引:先分别按照零指数幂法则、正整数指数幂法
则、负整数指数幂法则、绝对值的意义计算,
再进行加减.
解:原式=1-8-3+2=-8.对于底数是分数的负整数指数幂,我们可以将其转化
为这个数的倒数的正整数指数幂,即 .如
本例中 =3,这样就大大地简化了计算.知2-练1 (2015·厦门)2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
2 (中考·泰安)(-2)-2等于( )
A.-4 B.4 C.- D.
3 若(x-3)0-2(3x-6)-2有意义,则x的取值范围
是( )
A.x>3 B.x≠3且x≠2 C.x≠3或x≠2 D.x<23知识点整数指数幂的性质知3-导计算下列各式,你有什么发现?与同伴进行交流.
(1) 7-3÷ 7-5 ;
(2) 3-1÷ 36 ;
(3)
(4) (-8)0÷ (-8)-2 .
只要m,n都是整数,就有am ÷an=am-n成立!知2-练知3-讲在引进了零指数幂和负整数指数幂后,指数的范围已
经扩充到了全体整数,幂的运算性质仍然成立.即有:
(1)am·an=am+n;(2)(am)n=amn;(3)(ab)n=anbn;
(4)am÷an=am-n;(5) ;(6)a0=1.
(这里m,n为整数,a≠0,b≠0)
要点精析:(1)在幂的混合运算中,先计算乘方,再计
算乘除,最后计算加减.
(2)最后结果要化成正整数指数幂.
(3)a-p= 可变形为:a-p·ap=1或 =ap.知2-练知3-讲例6 计算:x2·x3÷x-4=________.
导引:x2·x3÷x-4=x2+3-(-4)=x9.x9运用同底数幂的乘除法法则进行计算,熟记法则并且
正确应用法则是解题的关键.知2-练知3-讲知2-练知3-讲例7 已知10m=3,10n=2,试求102m-n的值.
导引:逆用幂的乘方及同底数幂的除法法则,
进行运算即可.
解: 102m-n=(10m)2÷10n=9÷2=4.5 .
本题应用逆向思维法和代入法解答.先逆用同底数
幂的除法法则和幂的乘方,将所求代数式转化为关
于10m和10n的式子,再将10m和10n的值代入计算.知3-练1 (2016·潍坊)计算:20·2-3=( )
A.- B. C.0 D.8
2 (2015·河北)下列运算正确的是( )
A. B.6×107=6 000 000
C.(2a)2=2a2 D.a3·a2=a5
3 若下列运算正确的是( )
A.a6÷a2=a3 B.(ab2)2=ab4
C.2-3=-6 D.知3-练4 下列各式的计算中,不正确的个数是( )
①100÷10-1=10;
②10-4×(2×7)0=1 000;
③(-0.1)0÷(-2-1)-3=8;
④(-10)-4÷(-10-1)-4=-1.
A.4 B.3 C.2 D.1知3-练5 将 ,(-2)0,(-3)2这三个数按从小到大的顺序排列,正确的是( )
A.(-2)0< <(-3)2
B. <(-2)0<(-3)2
C.(-3)2<(-2)0<
D.(-2)0<(-3)2<1. 零指数幂:
任何不等于0的数的0次幂都等于1,即(a≠0).
2. 负整数指数幂:
(1)负整数指数幂的变形:a-n=
(a≠0,n是正整数).
(2)底数为正数的任何次幂都为正数;底数为负数的
奇次幂是负数,偶次幂是正数.
(3)运算结果要化为正整数指数幂.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
