2.1.4多项式的乘法 单项式与多项式相乘 同步练习
文档属性
| 名称 | 2.1.4多项式的乘法 单项式与多项式相乘 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 00:00:00 | ||
图片预览


文档简介
2.1 整式的乘法
第4课时 单项式与多项式相乘
核心笔记:
1.单项式乘多项式的法则:单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.字母表达式为
m=am+bm+cm.
2.几何背景图如图所示:
大长方形的面积等于三个小长方形的面积之和,即m=am+bm+cm.
基础训练
1.计算-x(x-y)的结果是( )
A.-x2-xy B.-x+xy
C.-x2+xy D.x2+xy
2.a2(-a+b-c)与-a(a2-ab+ac)的关系是( )
A.相等 B.符号相反
C.前式是后式的-a倍 D.以上结论都不对
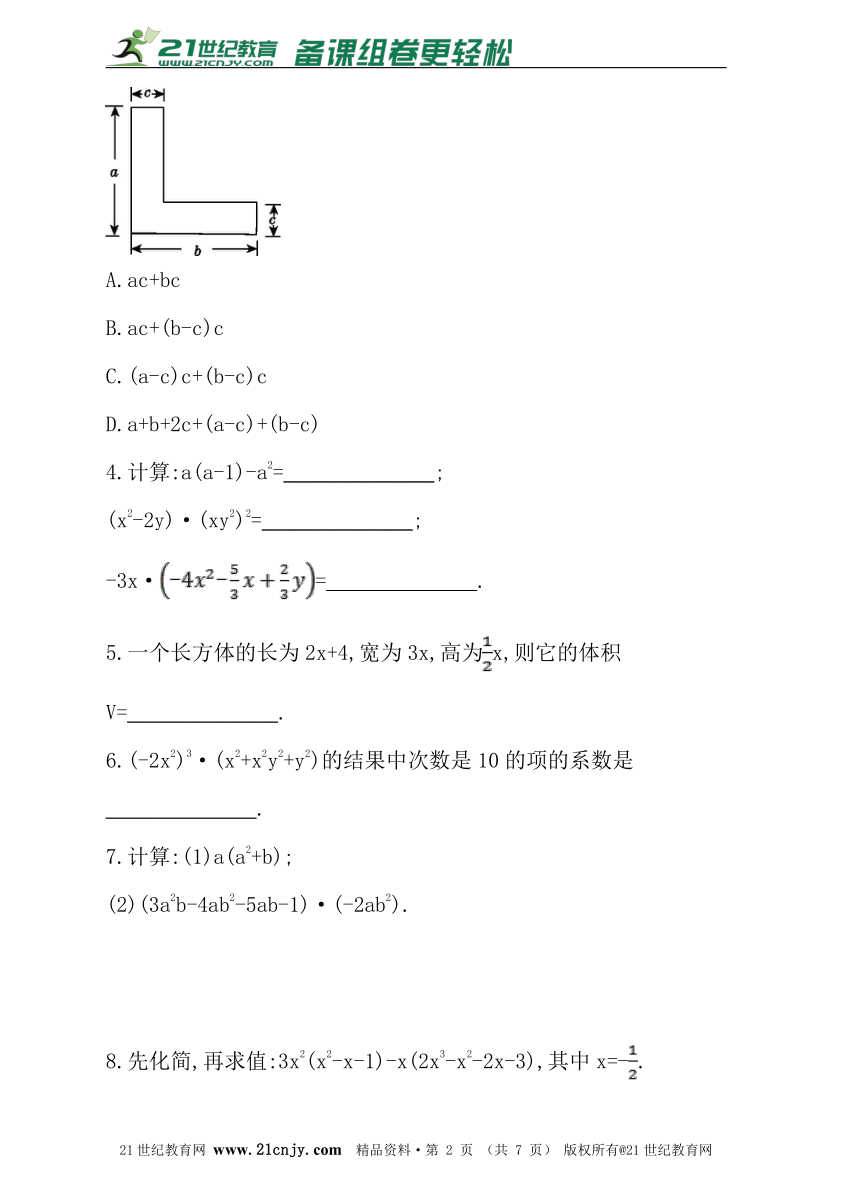
3.如图是L形钢条截面,它的面积为( )
A.ac+bc
B.ac+(b-c)c
C.(a-c)c+(b-c)c
D.a+b+2c+(a-c)+(b-c)
4.计算:a(a-1)-a2=______________;?
(x2-2y)·(xy2)2=______________;?
-3x·=______________.?
5.一个长方体的长为2x+4,宽为3x,高为x,则它的体积
V=______________.?
6.(-2x2)3·(x2+x2y2+y2)的结果中次数是10的项的系数是
______________.?
7.计算:(1)a(a2+b);
(2)(3a2b-4ab2-5ab-1)·(-2ab2).
8.先化简,再求值:3x2(x2-x-1)-x(2x3-x2-2x-3),其中x=-.
培优提升
1.计算x(1+x)-x(1-x)等于( )
A.2x B.2x2
C.0 D.-2x+2x2
2.已知-8xy除某一个多项式所得的商式是-xy+x2y-xy2,余式是3x3y2,则这个多项式是( )
A.4x2y2-13x3y2-14x2y3
B.4x2y2-15x3y2+14x2y3
C.4x2y2-15x3y2-14x3y3
D.4x2y2-15x3y3-14x2y3
3.已知计算(2-nx+3x2+mx3)·(-4x2)的结果中不含x5的项,则m等于
( )
A.0 B.1 C.-1 D.-0.25
4.计算:·(-2x)=_______________.?
5.一个长方体的长、宽、高分别是3x+1,2x和x,则它的表面积
是 .?
6.观察下列各式:1×3=12+2×1,2×4=22+2×2,3×5=32+2×3,…,请
你将猜想到的规律用自然数n(n≥1)表示出来: .?
7.现规定一种运算:a·b=ab+a-b,其中a,b为有理数,则
a·(b-1)+(b-a)·b= .
8.先化简,再求值:3(2x+1)+2(3-x),其中x=-1.
9.一住房的结构如图所示.
(1)这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是a元/m2,那么购买这种地砖至少需要多少元?
(2)已知房屋的高度为h m,现需要在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买这种壁纸至少需要多少元?(计算时不扣除门、窗所占的面积)
10.7张如图①的长为a,宽为b(a>b)的小长方形纸片,按图②的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足什么关系?
参考答案
【基础训练】
1.【答案】C
2.【答案】A
解:a2(-a+b-c)=-a3+a2b-a2c,-a(a2-ab+ac)=-a3+a2b-a2c,故相等.
3.【答案】B
4.【答案】-a;x4y4-2x2y5;12x3+5x2-2xy
5.【答案】3x3+6x2
6.【答案】-8
解:(-2x2)3·(x2+x2y2+y2)=-8x6·(x2+x2y2+y2)=-8x8-8x8y2-8x6y2,次数是10的项是-8x8y2,其系数是-8.
7.解:(1)a(a2+b) =a3+ab.
(2)(3a2b-4ab2-5ab-1)·(-2ab2)=-6a3b3+8a2b4+10a2b3+2ab2.
8.解: 3x2(x2-x-1)-x(2x3-x2-2x-3)
=3x4-3x3-3x2-2x4+x3+2x2+3x
=x4-2x3-x2+3x,
当x=-时,
原式=-2×-+3×=+--=-.
【培优提升】
1.【答案】B
解: x(1+x)-x(1-x)=x+x2-x+x2=2x2.
2.【答案】B
解:原多项式为
·(-8xy)+3x3y2=4x2y2-15x3y2+14x2y3.
3.【答案】A
4.【答案】-2x3-x2+2x
5.【答案】22x2+6x
解:长方体的表面积=2[2x(3x+1)+(3x+1)x+2x·x]
=2(6x2+2x+3x2+x+2x2)
=2(11x2+3x)
=22x2+6x.
6.【答案】n(n+2)=n2+2n
7.【答案】b2-a-b+1
解:a·(b-1)+(b-a)·b=a(b-1)+a-(b-1)+(b-a)b+(b-a)-b=b2-a-b+1.
8.解:原式=6x+3+6-2x=4x+9.
当x=-1时,原式=4×(-1)+9=5.
9.解:(1)客厅的面积+厨房的面积+卫生间的面积
=2x·4y+x·(4y-2y)+y·(4x-x-2x)=8xy+2xy+xy=11xy(m2).
11xy·a=11axy(元).
答:至少需要11xy m2的地砖,购买这种地砖至少需要11axy元.
(2)(2y+4x-2x)×2×h+(4y+2x)×2×h
=4yh+4xh+8yh+4xh
=12yh+8xh(m2).
(12yh+8xh)×b=12yhb+8xhb(元).
答:至少需要(12yh+8xh)m2的壁纸.购买这种壁纸至少需要
(12yhb+8xhb)元.
10.解:设BC的长度为x,左上角阴影部分的长为x-a,宽为3b;右下角阴影部分的长为x-4b,宽为a.
所以阴影部分面积之差
S=(x-a)3b-(x-4b)a=3bx-3ab-ax+4ab=(3b-a)x+ab.
因为S与x无关,所以3b-a=0,即a=3b.
第4课时 单项式与多项式相乘
核心笔记:
1.单项式乘多项式的法则:单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.字母表达式为
m=am+bm+cm.
2.几何背景图如图所示:
大长方形的面积等于三个小长方形的面积之和,即m=am+bm+cm.
基础训练
1.计算-x(x-y)的结果是( )
A.-x2-xy B.-x+xy
C.-x2+xy D.x2+xy
2.a2(-a+b-c)与-a(a2-ab+ac)的关系是( )
A.相等 B.符号相反
C.前式是后式的-a倍 D.以上结论都不对
3.如图是L形钢条截面,它的面积为( )
A.ac+bc
B.ac+(b-c)c
C.(a-c)c+(b-c)c
D.a+b+2c+(a-c)+(b-c)
4.计算:a(a-1)-a2=______________;?
(x2-2y)·(xy2)2=______________;?
-3x·=______________.?
5.一个长方体的长为2x+4,宽为3x,高为x,则它的体积
V=______________.?
6.(-2x2)3·(x2+x2y2+y2)的结果中次数是10的项的系数是
______________.?
7.计算:(1)a(a2+b);
(2)(3a2b-4ab2-5ab-1)·(-2ab2).
8.先化简,再求值:3x2(x2-x-1)-x(2x3-x2-2x-3),其中x=-.
培优提升
1.计算x(1+x)-x(1-x)等于( )
A.2x B.2x2
C.0 D.-2x+2x2
2.已知-8xy除某一个多项式所得的商式是-xy+x2y-xy2,余式是3x3y2,则这个多项式是( )
A.4x2y2-13x3y2-14x2y3
B.4x2y2-15x3y2+14x2y3
C.4x2y2-15x3y2-14x3y3
D.4x2y2-15x3y3-14x2y3
3.已知计算(2-nx+3x2+mx3)·(-4x2)的结果中不含x5的项,则m等于
( )
A.0 B.1 C.-1 D.-0.25
4.计算:·(-2x)=_______________.?
5.一个长方体的长、宽、高分别是3x+1,2x和x,则它的表面积
是 .?
6.观察下列各式:1×3=12+2×1,2×4=22+2×2,3×5=32+2×3,…,请
你将猜想到的规律用自然数n(n≥1)表示出来: .?
7.现规定一种运算:a·b=ab+a-b,其中a,b为有理数,则
a·(b-1)+(b-a)·b= .
8.先化简,再求值:3(2x+1)+2(3-x),其中x=-1.
9.一住房的结构如图所示.
(1)这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是a元/m2,那么购买这种地砖至少需要多少元?
(2)已知房屋的高度为h m,现需要在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买这种壁纸至少需要多少元?(计算时不扣除门、窗所占的面积)
10.7张如图①的长为a,宽为b(a>b)的小长方形纸片,按图②的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足什么关系?
参考答案
【基础训练】
1.【答案】C
2.【答案】A
解:a2(-a+b-c)=-a3+a2b-a2c,-a(a2-ab+ac)=-a3+a2b-a2c,故相等.
3.【答案】B
4.【答案】-a;x4y4-2x2y5;12x3+5x2-2xy
5.【答案】3x3+6x2
6.【答案】-8
解:(-2x2)3·(x2+x2y2+y2)=-8x6·(x2+x2y2+y2)=-8x8-8x8y2-8x6y2,次数是10的项是-8x8y2,其系数是-8.
7.解:(1)a(a2+b) =a3+ab.
(2)(3a2b-4ab2-5ab-1)·(-2ab2)=-6a3b3+8a2b4+10a2b3+2ab2.
8.解: 3x2(x2-x-1)-x(2x3-x2-2x-3)
=3x4-3x3-3x2-2x4+x3+2x2+3x
=x4-2x3-x2+3x,
当x=-时,
原式=-2×-+3×=+--=-.
【培优提升】
1.【答案】B
解: x(1+x)-x(1-x)=x+x2-x+x2=2x2.
2.【答案】B
解:原多项式为
·(-8xy)+3x3y2=4x2y2-15x3y2+14x2y3.
3.【答案】A
4.【答案】-2x3-x2+2x
5.【答案】22x2+6x
解:长方体的表面积=2[2x(3x+1)+(3x+1)x+2x·x]
=2(6x2+2x+3x2+x+2x2)
=2(11x2+3x)
=22x2+6x.
6.【答案】n(n+2)=n2+2n
7.【答案】b2-a-b+1
解:a·(b-1)+(b-a)·b=a(b-1)+a-(b-1)+(b-a)b+(b-a)-b=b2-a-b+1.
8.解:原式=6x+3+6-2x=4x+9.
当x=-1时,原式=4×(-1)+9=5.
9.解:(1)客厅的面积+厨房的面积+卫生间的面积
=2x·4y+x·(4y-2y)+y·(4x-x-2x)=8xy+2xy+xy=11xy(m2).
11xy·a=11axy(元).
答:至少需要11xy m2的地砖,购买这种地砖至少需要11axy元.
(2)(2y+4x-2x)×2×h+(4y+2x)×2×h
=4yh+4xh+8yh+4xh
=12yh+8xh(m2).
(12yh+8xh)×b=12yhb+8xhb(元).
答:至少需要(12yh+8xh)m2的壁纸.购买这种壁纸至少需要
(12yhb+8xhb)元.
10.解:设BC的长度为x,左上角阴影部分的长为x-a,宽为3b;右下角阴影部分的长为x-4b,宽为a.
所以阴影部分面积之差
S=(x-a)3b-(x-4b)a=3bx-3ab-ax+4ab=(3b-a)x+ab.
因为S与x无关,所以3b-a=0,即a=3b.
