2.2.1平方差公式 同步练习
图片预览

文档简介
2.2 乘法公式
第1课时 平方差公式
核心笔记: 两个数的和与这两个数的差的积等于这两个数的平方差,即:(a+b)(a-b)=a2-b2,所以,我们把这个公式叫做平方差公式.平方差公式可以形象记忆为:(□+△)(□-△)=□2-△2.
基础训练
1.下列各式中能用平方差公式进行计算的有( )
①; ②(3x-4y)(-4y-3x);
③(3-x+y)(3+x+y); ④(100+4)×(100-4).
A.1个 B.2个 C.3个 D.4个
2.计算(x+1)(x-1)(x2+1),结果正确的是( )
A.x4-1 B.x4+1
C.(x-1)4 D.(x+1)4
3.等式(-a-b)( )=a2-b2中,括号内应填( )
A.a-b B.-a+b
C.-a-b D.a+b
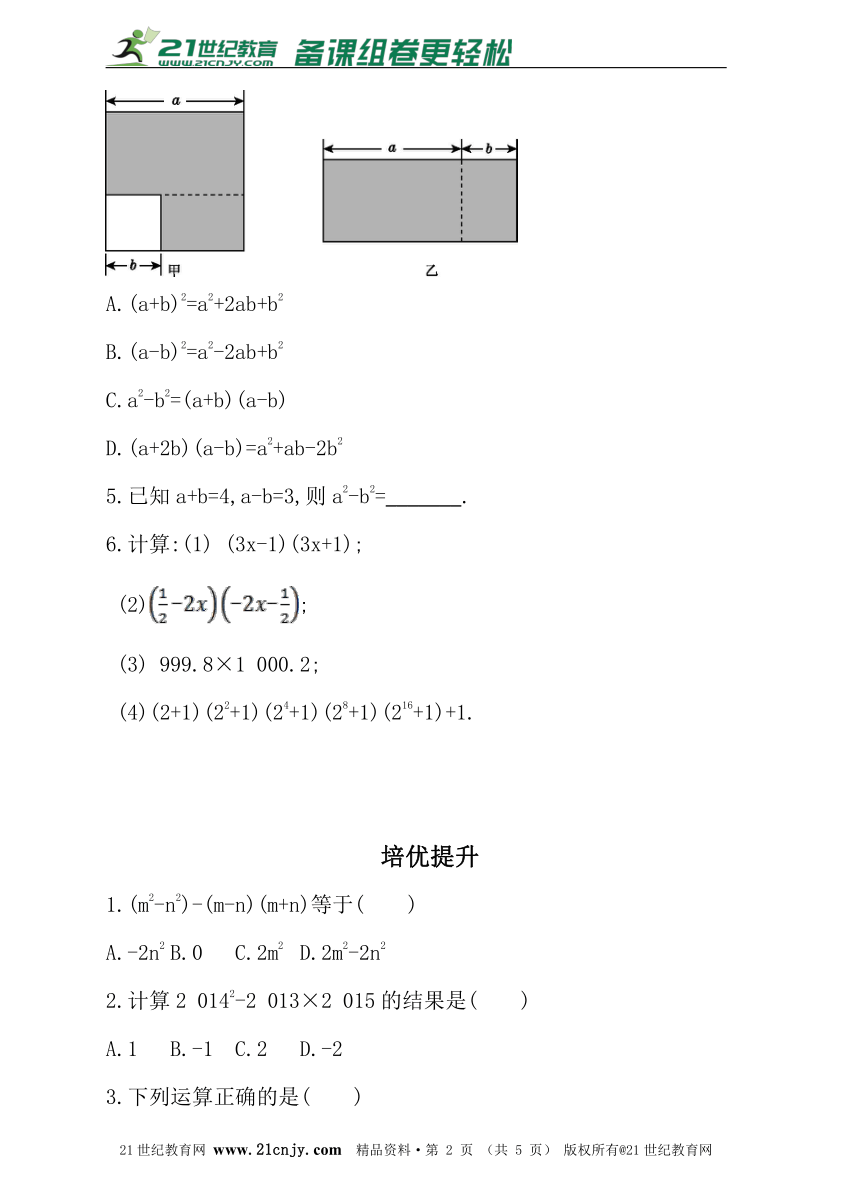
4.在边长为a的大正方形中剪去一个边长为b的小正方形(a>b)(如图甲),把余下的部分沿虚线剪开,并拼成一个长方形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a-b)2=a2-2ab+b2
C.a2-b2=(a+b)(a-b)
D.(a+2b)(a-b)=a2+ab-2b2
5.已知a+b=4,a-b=3,则a2-b2=_______.?
6.计算:(1) (3x-1)(3x+1);
(2);
(3) 999.8×1 000.2;
(4)(2+1)(22+1)(24+1)(28+1)(216+1)+1.
培优提升
1.(m2-n2)-(m-n)(m+n)等于( )
A.-2n2 B.0 C.2m2 D.2m2-2n2
2.计算2 0142-2 013×2 015的结果是( )
A.1 B.-1 C.2 D.-2
3.下列运算正确的是( )
A.(-3mn)2=-6m2n2 B.4x4+2x4+x4=6x4
C.(-xy)·xy=-x2y2 D.(a-b)(-a-b)=a2-b2
4. (x+1)(x-1)-x2化简为( )
A.1 B.-1 C.x2 D.-2x2
5.观察下列等式19×21=202-1,28×32=302-22,37×43=402-32,…,仿照上述的表示方法可得:2 000×2 014=____________.?
6.若3x-1=0,则(x-1)(x+1)-x(x-3)的值为____________.?
7.解方程:(4x+1)(4x-1)+(3x-2)2-(5x+2)2=-33.
8.已知2a2+3a-6=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值.
9.实际应用题 某木工师傅根据需要将一块边长为a m的正方形木板的两边(对边)增加3 m,另两边(对边)减少3 m,得到一块长方形木板,求长方形木板的面积,并比较长方形木板的面积与正方形木板的面积的大小,两木板面积相差多少?
参考答案
【基础训练】
1.【答案】D
解:①④可以直接用平方差公式进行计算;②变形为
-(3x-4y)(3x+4y),③变形为[(3+y)-x][(3+y)+x]后都可以用平方差公式进行计算.所以选D.
2.【答案】A
解:连续两次运用平方差公式计算即可.
3.【答案】B 4.【答案】C 5.【答案】12
6.解:(1) (3x-1)(3x+1)=9x2-1.
(2)=(-2x)2-=4x2-.
(3)999.8×1 000.2=(1 000-0.2)(1 000+0.2)=1 0002-0.22=999 999.96.
(4)(2+1)(22+1)(24+1)(28+1)(216+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)+1=232-1+1=232.
【培优提升】
1.【答案】B
解:(m2-n2)-(m-n)(m+n)=(m2-n2)-(m2-n2)=m2-n2-m2+n2=0,故选B.
2.【答案】A
解:2 0142-2 013×2 015=2 0142-(2 014-1)×(2 014+1)=2 0142-(2 0142-1)=1.
3.【答案】C
4.【答案】B
解:(x+1)(x-1)-x2=x2-1-x2=-1.
5.【答案】20072-72 解:2000=2 007-7,2014=2007+7.
6.【答案】0
解:原式=x2-1-x2+3x=3x-1=0.
7.解:原方程左边
=(4x+1)(4x-1)+(3x-2)2-(5x+2)2=16x2-1+(3x-2+5x+2)(3x-2-5x-2)=16x2-1+8x(-2x-4)=-32x-1,所以原方程可化为-32x-1=-33,解得x=1.
8.解:3a(2a+1)-(2a+1)(2a-1)
=6a2+3a-4a2+1
=2a2+3a+1.
因为2a2+3a-6=0,
所以2a2+3a=6.
所以原式=7.
9.解:长方形木板的面积是(a+3)(a-3)=a2-9(m2),
正方形木板的面积是a2 m2,所以正方形木板的面积大.
两木板面积相差a2-(a2-9)=a2-a2+9=9(m2).
第1课时 平方差公式
核心笔记: 两个数的和与这两个数的差的积等于这两个数的平方差,即:(a+b)(a-b)=a2-b2,所以,我们把这个公式叫做平方差公式.平方差公式可以形象记忆为:(□+△)(□-△)=□2-△2.
基础训练
1.下列各式中能用平方差公式进行计算的有( )
①; ②(3x-4y)(-4y-3x);
③(3-x+y)(3+x+y); ④(100+4)×(100-4).
A.1个 B.2个 C.3个 D.4个
2.计算(x+1)(x-1)(x2+1),结果正确的是( )
A.x4-1 B.x4+1
C.(x-1)4 D.(x+1)4
3.等式(-a-b)( )=a2-b2中,括号内应填( )
A.a-b B.-a+b
C.-a-b D.a+b
4.在边长为a的大正方形中剪去一个边长为b的小正方形(a>b)(如图甲),把余下的部分沿虚线剪开,并拼成一个长方形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a-b)2=a2-2ab+b2
C.a2-b2=(a+b)(a-b)
D.(a+2b)(a-b)=a2+ab-2b2
5.已知a+b=4,a-b=3,则a2-b2=_______.?
6.计算:(1) (3x-1)(3x+1);
(2);
(3) 999.8×1 000.2;
(4)(2+1)(22+1)(24+1)(28+1)(216+1)+1.
培优提升
1.(m2-n2)-(m-n)(m+n)等于( )
A.-2n2 B.0 C.2m2 D.2m2-2n2
2.计算2 0142-2 013×2 015的结果是( )
A.1 B.-1 C.2 D.-2
3.下列运算正确的是( )
A.(-3mn)2=-6m2n2 B.4x4+2x4+x4=6x4
C.(-xy)·xy=-x2y2 D.(a-b)(-a-b)=a2-b2
4. (x+1)(x-1)-x2化简为( )
A.1 B.-1 C.x2 D.-2x2
5.观察下列等式19×21=202-1,28×32=302-22,37×43=402-32,…,仿照上述的表示方法可得:2 000×2 014=____________.?
6.若3x-1=0,则(x-1)(x+1)-x(x-3)的值为____________.?
7.解方程:(4x+1)(4x-1)+(3x-2)2-(5x+2)2=-33.
8.已知2a2+3a-6=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值.
9.实际应用题 某木工师傅根据需要将一块边长为a m的正方形木板的两边(对边)增加3 m,另两边(对边)减少3 m,得到一块长方形木板,求长方形木板的面积,并比较长方形木板的面积与正方形木板的面积的大小,两木板面积相差多少?
参考答案
【基础训练】
1.【答案】D
解:①④可以直接用平方差公式进行计算;②变形为
-(3x-4y)(3x+4y),③变形为[(3+y)-x][(3+y)+x]后都可以用平方差公式进行计算.所以选D.
2.【答案】A
解:连续两次运用平方差公式计算即可.
3.【答案】B 4.【答案】C 5.【答案】12
6.解:(1) (3x-1)(3x+1)=9x2-1.
(2)=(-2x)2-=4x2-.
(3)999.8×1 000.2=(1 000-0.2)(1 000+0.2)=1 0002-0.22=999 999.96.
(4)(2+1)(22+1)(24+1)(28+1)(216+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)+1=232-1+1=232.
【培优提升】
1.【答案】B
解:(m2-n2)-(m-n)(m+n)=(m2-n2)-(m2-n2)=m2-n2-m2+n2=0,故选B.
2.【答案】A
解:2 0142-2 013×2 015=2 0142-(2 014-1)×(2 014+1)=2 0142-(2 0142-1)=1.
3.【答案】C
4.【答案】B
解:(x+1)(x-1)-x2=x2-1-x2=-1.
5.【答案】20072-72 解:2000=2 007-7,2014=2007+7.
6.【答案】0
解:原式=x2-1-x2+3x=3x-1=0.
7.解:原方程左边
=(4x+1)(4x-1)+(3x-2)2-(5x+2)2=16x2-1+(3x-2+5x+2)(3x-2-5x-2)=16x2-1+8x(-2x-4)=-32x-1,所以原方程可化为-32x-1=-33,解得x=1.
8.解:3a(2a+1)-(2a+1)(2a-1)
=6a2+3a-4a2+1
=2a2+3a+1.
因为2a2+3a-6=0,
所以2a2+3a=6.
所以原式=7.
9.解:长方形木板的面积是(a+3)(a-3)=a2-9(m2),
正方形木板的面积是a2 m2,所以正方形木板的面积大.
两木板面积相差a2-(a2-9)=a2-a2+9=9(m2).
