2.2.2完全平方公式 同步练习
图片预览


文档简介
2.2 乘法公式
第2课时 完全平方公式
核心笔记:
1.两数和的平方:(a+b)2=a2+2ab+b2,两数差的平方:(a-b)2=a2-2ab+b2.即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.这两个公式可以合在一起写:(a±b)2=a2±2ab+b2.为便于记忆,可叙述为:“首平方、尾平方,2倍乘积在中央”.
2.几何背景:如图,大正方形的面积S可以表示为(a+b)2,也可以表示为SⅠ+SⅡ+SⅢ+SⅣ,即S=a2+ab+ab+b2=a2+2ab+b2.从而验证了完全平方公式(a+b)2=a2+2ab+b2.
基础训练
1.下列运算正确的是( )
A.2a+3b=5ab B.5a-2a=3a
C.a2·a3=a6 D.(a+b)2=a2+b2
2.(-x2-y)2 等于( )
A.-x2-2xy+y2 B.-x4-2x2y+y2
C.x4+2x2y+y2 D.x4-2xy+y2
3.如图,大正方形边长为a+b,中间空的小正方形边长为a-b,则阴影部分面积是( )
A.2ab B.4ab
C. a2+b2 D. a2-b2
4.化简:(a-b)2+a(2b-a)=________.?
5.若x2-ax+25是一个完全平方式,则a=________.?
6. (x-2y)2+ =(x+2y)2.?
7.计算:(1)(5+3p)2; (2)(2x-3y)2;
(3)(-2a-b)2; (4)2012.
8.先化简,再求值:(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
培优提升
1.下列运算中,错误的有( )
①(2x+y)2=4x2+y2;②(a-3b)2=a2-9b2 ;③(-x-y)2=x2-2xy+y2;④=x2-x+.
A.1个 B.2个 C.3个 D.4个
2.若要得到(a-b)2,则a2+3ab+b2需要加上( )
A.-ab B.-3ab C.-5ab D.-4ab
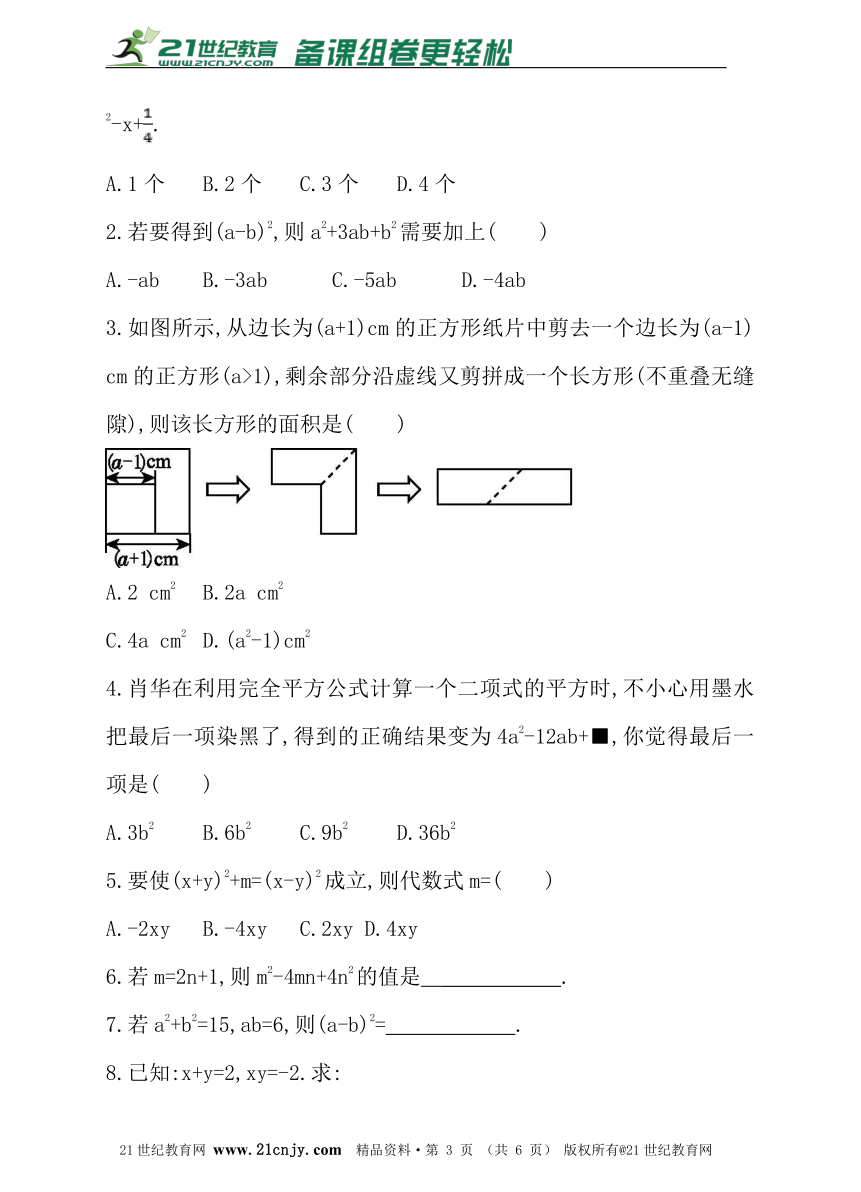
3.如图所示,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1) cm的正方形(a>1),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则该长方形的面积是( )
A.2 cm2 B.2a cm2
C.4a cm2 D.(a2-1)cm2
4.肖华在利用完全平方公式计算一个二项式的平方时,不小心用墨水把最后一项染黑了,得到的正确结果变为4a2-12ab+■,你觉得最后一项是( )
A.3b2 B.6b2 C.9b2 D.36b2
5.要使(x+y)2+m=(x-y)2成立,则代数式m=( )
A.-2xy B.-4xy C.2xy D.4xy
6.若m=2n+1,则m2-4mn+4n2的值是 ___________.?
7.若a2+b2=15,ab=6,则(a-b)2=____________.?
8.已知:x+y=2,xy=-2.求:
(1)x2+y2的值;
(2)(x-y)2的值.
9.如图,AB=a,P是线段AB上一点,分别以AP,BP为边作正方形.
(1)设AP=x,求两个正方形的面积之和S;
(2)当AP分别为a和a时,两个正方形的面积的和分别为S1和S2,比较S1和S2的大小.
参考答案
【基础训练】
1.【答案】B 2.【答案】C
3.【答案】B
解:阴影部分的面积=大正方形的面积-小正方形的面积=(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=4ab.
4.【答案】b2
解:原式=a2-2ab+b2+2ab-a2=b2.
5.【答案】±10 6.【答案】8xy
7.解:(1)(5+3p)2=52+2×5×3p+(3p)2=25+30p+9p2.
(2)(2x-3y)2=(2x)2-2×(2x)×(3y)+(3y)2=4x2-12xy+9y2.
(3)(-2a-b)2=(-2a)2+2×(-2a)·(-b)+(-b)2=4a2+4ab+b2.
(4)2012=(200+1)2=2002+2×200×1+12=40 401.
8.解:原式=a2+4ab+4b2+b2-a2=4ab+5b2.
当a=-1,b=2时,原式=4×(-1)×2+5×22=-8+20=12.
【培优提升】
1.【答案】C
解:①中运算结果应是4x2+4xy+y2,所以错误;②中运算结果应是a2-6ab+9b2,所以错误;③中运算结果应是x2+2xy+y2,所以错误;④中运算结果正确.故选C.
2.【答案】C
解:计算(a-b)2-(a2+3ab+b2)即得结果.
3.【答案】C
解:根据题意,得长方形的面积是
(a+1)2-(a-1)2=a2+2a+1-(a2-2a+1)=4a(cm2),故选C.
4.【答案】C
5.【答案】B
解:由题意可得m=(x-y)2-(x+y)2=x2-2xy+y2-(x2+2xy+y2)=-4xy.
6.【答案】1
解:m2-4mn+4n2=(m-2n)2=1.
7.【答案】3
解:(a-b)2=a2-2ab+b2=a2+b2-2ab=15-12=3.
8.解:(1)原式=(x+y)2-2xy,当x+y=2,xy=-2时,原式=22-2×(-2)=8.
(2)原式=x2+y2-2xy,
因为x2+y2=8,xy=-2,所以原式=8-2×(-2)=12.
9.解:(1)小正方形的面积=x2,大正方形的面积=(a-x)2,所以面积之和S=x2+(a-x)2=x2+a2-2ax+x2=2x2-2ax+a2.
(2)当AP=a时,将x=a代入2x2-2ax+a2得S1=a2;当AP=a时,将x=a代入2x2-2ax+a2得S2=a2,因为a2>a2,所以S1>S2.
第2课时 完全平方公式
核心笔记:
1.两数和的平方:(a+b)2=a2+2ab+b2,两数差的平方:(a-b)2=a2-2ab+b2.即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.这两个公式可以合在一起写:(a±b)2=a2±2ab+b2.为便于记忆,可叙述为:“首平方、尾平方,2倍乘积在中央”.
2.几何背景:如图,大正方形的面积S可以表示为(a+b)2,也可以表示为SⅠ+SⅡ+SⅢ+SⅣ,即S=a2+ab+ab+b2=a2+2ab+b2.从而验证了完全平方公式(a+b)2=a2+2ab+b2.
基础训练
1.下列运算正确的是( )
A.2a+3b=5ab B.5a-2a=3a
C.a2·a3=a6 D.(a+b)2=a2+b2
2.(-x2-y)2 等于( )
A.-x2-2xy+y2 B.-x4-2x2y+y2
C.x4+2x2y+y2 D.x4-2xy+y2
3.如图,大正方形边长为a+b,中间空的小正方形边长为a-b,则阴影部分面积是( )
A.2ab B.4ab
C. a2+b2 D. a2-b2
4.化简:(a-b)2+a(2b-a)=________.?
5.若x2-ax+25是一个完全平方式,则a=________.?
6. (x-2y)2+ =(x+2y)2.?
7.计算:(1)(5+3p)2; (2)(2x-3y)2;
(3)(-2a-b)2; (4)2012.
8.先化简,再求值:(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
培优提升
1.下列运算中,错误的有( )
①(2x+y)2=4x2+y2;②(a-3b)2=a2-9b2 ;③(-x-y)2=x2-2xy+y2;④=x2-x+.
A.1个 B.2个 C.3个 D.4个
2.若要得到(a-b)2,则a2+3ab+b2需要加上( )
A.-ab B.-3ab C.-5ab D.-4ab
3.如图所示,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1) cm的正方形(a>1),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则该长方形的面积是( )
A.2 cm2 B.2a cm2
C.4a cm2 D.(a2-1)cm2
4.肖华在利用完全平方公式计算一个二项式的平方时,不小心用墨水把最后一项染黑了,得到的正确结果变为4a2-12ab+■,你觉得最后一项是( )
A.3b2 B.6b2 C.9b2 D.36b2
5.要使(x+y)2+m=(x-y)2成立,则代数式m=( )
A.-2xy B.-4xy C.2xy D.4xy
6.若m=2n+1,则m2-4mn+4n2的值是 ___________.?
7.若a2+b2=15,ab=6,则(a-b)2=____________.?
8.已知:x+y=2,xy=-2.求:
(1)x2+y2的值;
(2)(x-y)2的值.
9.如图,AB=a,P是线段AB上一点,分别以AP,BP为边作正方形.
(1)设AP=x,求两个正方形的面积之和S;
(2)当AP分别为a和a时,两个正方形的面积的和分别为S1和S2,比较S1和S2的大小.
参考答案
【基础训练】
1.【答案】B 2.【答案】C
3.【答案】B
解:阴影部分的面积=大正方形的面积-小正方形的面积=(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=4ab.
4.【答案】b2
解:原式=a2-2ab+b2+2ab-a2=b2.
5.【答案】±10 6.【答案】8xy
7.解:(1)(5+3p)2=52+2×5×3p+(3p)2=25+30p+9p2.
(2)(2x-3y)2=(2x)2-2×(2x)×(3y)+(3y)2=4x2-12xy+9y2.
(3)(-2a-b)2=(-2a)2+2×(-2a)·(-b)+(-b)2=4a2+4ab+b2.
(4)2012=(200+1)2=2002+2×200×1+12=40 401.
8.解:原式=a2+4ab+4b2+b2-a2=4ab+5b2.
当a=-1,b=2时,原式=4×(-1)×2+5×22=-8+20=12.
【培优提升】
1.【答案】C
解:①中运算结果应是4x2+4xy+y2,所以错误;②中运算结果应是a2-6ab+9b2,所以错误;③中运算结果应是x2+2xy+y2,所以错误;④中运算结果正确.故选C.
2.【答案】C
解:计算(a-b)2-(a2+3ab+b2)即得结果.
3.【答案】C
解:根据题意,得长方形的面积是
(a+1)2-(a-1)2=a2+2a+1-(a2-2a+1)=4a(cm2),故选C.
4.【答案】C
5.【答案】B
解:由题意可得m=(x-y)2-(x+y)2=x2-2xy+y2-(x2+2xy+y2)=-4xy.
6.【答案】1
解:m2-4mn+4n2=(m-2n)2=1.
7.【答案】3
解:(a-b)2=a2-2ab+b2=a2+b2-2ab=15-12=3.
8.解:(1)原式=(x+y)2-2xy,当x+y=2,xy=-2时,原式=22-2×(-2)=8.
(2)原式=x2+y2-2xy,
因为x2+y2=8,xy=-2,所以原式=8-2×(-2)=12.
9.解:(1)小正方形的面积=x2,大正方形的面积=(a-x)2,所以面积之和S=x2+(a-x)2=x2+a2-2ax+x2=2x2-2ax+a2.
(2)当AP=a时,将x=a代入2x2-2ax+a2得S1=a2;当AP=a时,将x=a代入2x2-2ax+a2得S2=a2,因为a2>a2,所以S1>S2.
