4.1.2 相交直线所成的角 同步练习
文档属性
| 名称 | 4.1.2 相交直线所成的角 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 15:31:29 | ||
图片预览


文档简介
4.1.2 相交直线所成的角
核心笔记: 1.对顶角:两个角有共同的顶点,且其中一个角的两边分别是另一个角两边的反向延长线,这样的两个角叫做对顶角.
2.对顶角的性质:对顶角相等.
3.同位角:在截线的同侧且在被截两直线的同一方.
4.内错角:在截线的两侧且在被截两直线之间(内部).
5.同旁内角:在截线的同侧且在被截两直线之间(内部).
基础训练
1.下列图形中,∠1与∠2是对顶角的是( )
2.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
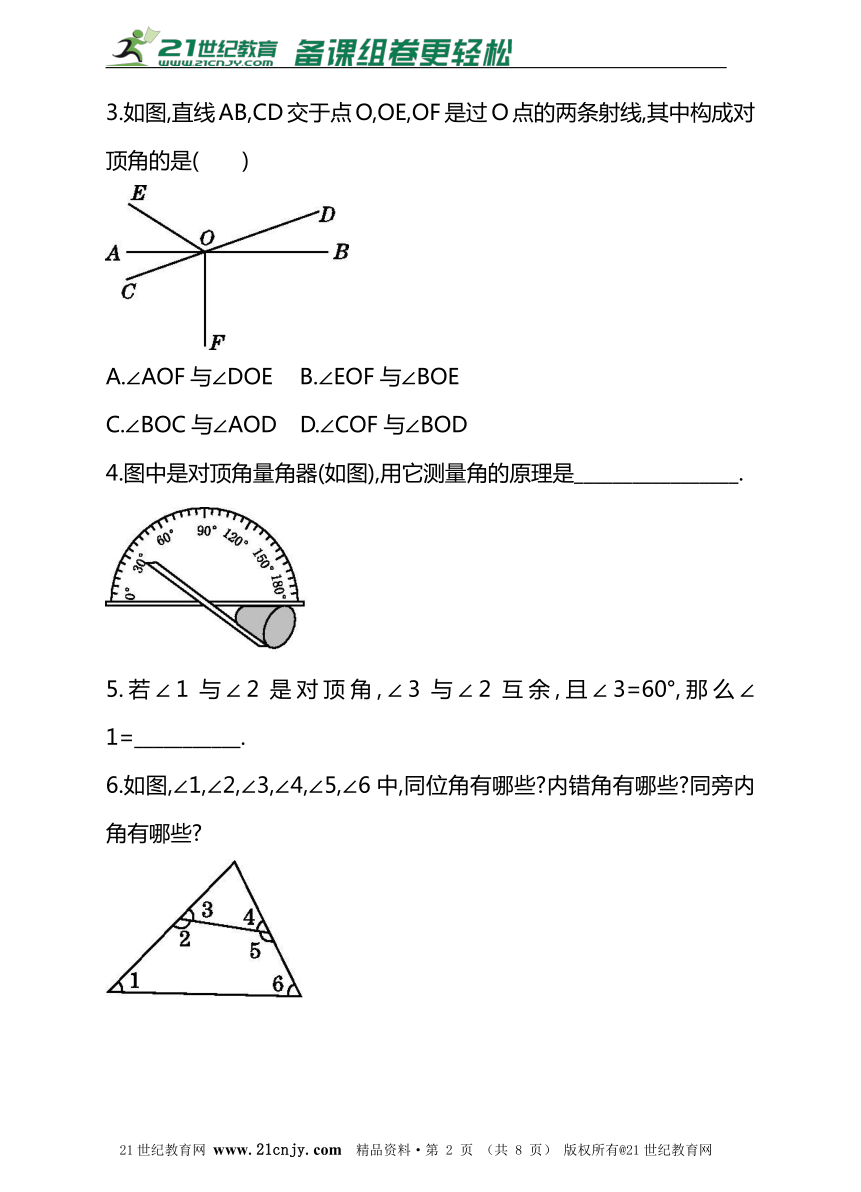
3.如图,直线AB,CD交于点O,OE,OF是过O点的两条射线,其中构成对顶角的是( )
A.∠AOF与∠DOE B.∠EOF与∠BOE
C.∠BOC与∠AOD D.∠COF与∠BOD
4.图中是对顶角量角器(如图),用它测量角的原理是_________________.?
5.若∠1与∠2是对顶角,∠3与∠2互余,且∠3=60°,那么∠1=___________.?
6.如图,∠1,∠2,∠3,∠4,∠5,∠6中,同位角有哪些?内错角有哪些?同旁内角有哪些?
7.如图,已知直线AD与BE相交于O,∠DOE与∠COE互余,∠COE=60°,求∠AOB的度数.
培优提升
1.下列说法中正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个
C.3个 D.4个
2.如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3
C.∠4 D.∠5
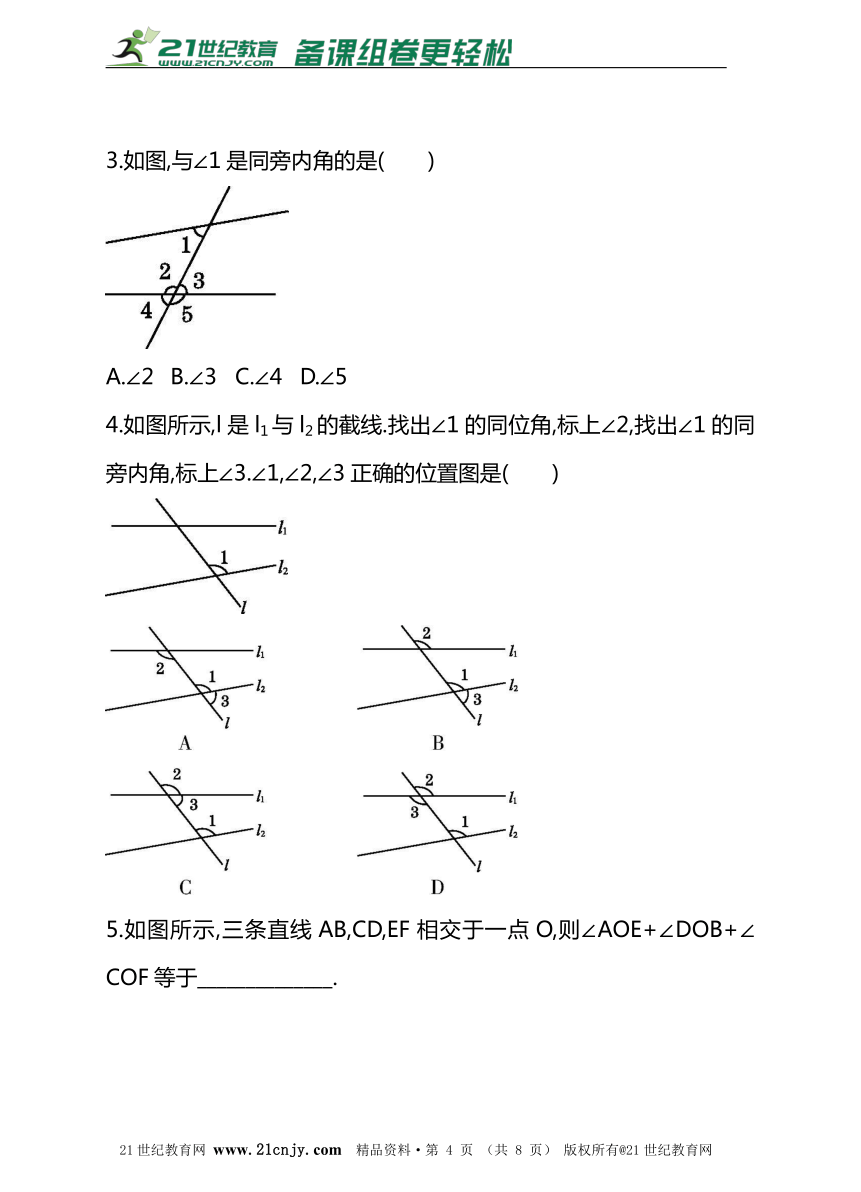
3.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图所示,l是l1与l2的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.∠1,∠2,∠3正确的位置图是( )21世纪教育网版权所有
5.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于______________.?21教育网
6.如图,直线AB,CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE=_____________.?21·cn·jy·com
7.已知,如图,直线AB,CD被EF所截,∠1=∠2.试说明:∠3+∠4=180°.
8.如图,直线AB,CD相交于点O,OE平分∠BOD,且∠AOC=∠AOD-80°,求∠AOE的度数.【来源:21·世纪·教育·网】
9.如图所示,三条直线AB,CD,EF相交于点O,找出图中的对顶角.猜想:如果n条直线相交于一点,那么有多少对对顶角?(n>1,且n为正整数)
参考答案
【基础训练】
1.【答案】C 2.【答案】A 3.【答案】C
4.【答案】对顶角相等
5.【答案】30°
解:因为∠3+∠2=90°,∠3=60°,所以∠2=30°,又因为∠1=∠2(对顶角相等),所以∠1=30°.2·1·c·n·j·y
6.解:同位角有:∠1和∠3,∠4和∠6.
内错角有:∠2和∠4,∠5和∠3.
同旁内角有:∠3和∠4,∠1和∠2,∠2和∠5,∠5和∠6,∠1和∠6.
7.解:因为∠DOE和∠COE互余,
所以∠DOE+∠COE=90°.
因为∠COE=60°,
所以∠DOE=30°.
因为∠DOE=∠AOB,
所以∠AOB=30°.
【培优训练】
1.【答案】B
解:①③正确.
2.【答案】A 3.【答案】A 4.【答案】C
5.【答案】180°
解:因为∠COF=∠EOD,所以
∠AOE+∠DOB+∠COF=∠AOE+∠DOB+∠EOD=180°.
6.【答案】40°
解:因为∠BOD=40°,所以∠AOC=∠BOD=40°,因为OA平分∠COE,所以∠AOE=∠AOC=40°.21cnjy.com
7.解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3(等量代换).
因为∠2+∠4=180°(平角定义),
所以∠3+∠4=180°(等量代换).
8.解:由题图知,∠AOC与∠AOD互补,即∠AOC+∠AOD=180°,又∠AOC=∠AOD-80°,所以∠AOC+80°+∠AOC=180°,所以2∠AOC=100°,即∠AOC=50°,又因为∠AOC与∠BOD是对顶角,所以∠BOD=∠AOC=50°.因为OE平分∠BOD,所以∠BOE=∠BOD=25°,所以∠AOE=180°-∠BOE=180°-25°=155°.www.21-cn-jy.com
9.解:题图中的对顶角有:∠AOC与∠BOD,∠BOC与∠AOD,∠AOE与∠BOF,∠EOD与∠COF,∠EOB与∠AOF,∠EOC与∠DOF,共6对.
n条直线相交于一点,共有[2+4+6+8+…+2(n-1)]对对顶角.
而2=1×2,2+4=6=2×3,2+4+6=12=3×4,…,
故[2+4+6+8+…+2(n-1)]=(n-1)n=n2-n.
即n条直线相交于一点,共有(n2-n)对对顶角.
分析:本题为探究题,应从最简单的情况入手,观察对顶角对数增加的规律,从而解决问题.
核心笔记: 1.对顶角:两个角有共同的顶点,且其中一个角的两边分别是另一个角两边的反向延长线,这样的两个角叫做对顶角.
2.对顶角的性质:对顶角相等.
3.同位角:在截线的同侧且在被截两直线的同一方.
4.内错角:在截线的两侧且在被截两直线之间(内部).
5.同旁内角:在截线的同侧且在被截两直线之间(内部).
基础训练
1.下列图形中,∠1与∠2是对顶角的是( )
2.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
3.如图,直线AB,CD交于点O,OE,OF是过O点的两条射线,其中构成对顶角的是( )
A.∠AOF与∠DOE B.∠EOF与∠BOE
C.∠BOC与∠AOD D.∠COF与∠BOD
4.图中是对顶角量角器(如图),用它测量角的原理是_________________.?
5.若∠1与∠2是对顶角,∠3与∠2互余,且∠3=60°,那么∠1=___________.?
6.如图,∠1,∠2,∠3,∠4,∠5,∠6中,同位角有哪些?内错角有哪些?同旁内角有哪些?
7.如图,已知直线AD与BE相交于O,∠DOE与∠COE互余,∠COE=60°,求∠AOB的度数.
培优提升
1.下列说法中正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个
C.3个 D.4个
2.如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3
C.∠4 D.∠5
3.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图所示,l是l1与l2的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.∠1,∠2,∠3正确的位置图是( )21世纪教育网版权所有
5.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于______________.?21教育网
6.如图,直线AB,CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE=_____________.?21·cn·jy·com
7.已知,如图,直线AB,CD被EF所截,∠1=∠2.试说明:∠3+∠4=180°.
8.如图,直线AB,CD相交于点O,OE平分∠BOD,且∠AOC=∠AOD-80°,求∠AOE的度数.【来源:21·世纪·教育·网】
9.如图所示,三条直线AB,CD,EF相交于点O,找出图中的对顶角.猜想:如果n条直线相交于一点,那么有多少对对顶角?(n>1,且n为正整数)
参考答案
【基础训练】
1.【答案】C 2.【答案】A 3.【答案】C
4.【答案】对顶角相等
5.【答案】30°
解:因为∠3+∠2=90°,∠3=60°,所以∠2=30°,又因为∠1=∠2(对顶角相等),所以∠1=30°.2·1·c·n·j·y
6.解:同位角有:∠1和∠3,∠4和∠6.
内错角有:∠2和∠4,∠5和∠3.
同旁内角有:∠3和∠4,∠1和∠2,∠2和∠5,∠5和∠6,∠1和∠6.
7.解:因为∠DOE和∠COE互余,
所以∠DOE+∠COE=90°.
因为∠COE=60°,
所以∠DOE=30°.
因为∠DOE=∠AOB,
所以∠AOB=30°.
【培优训练】
1.【答案】B
解:①③正确.
2.【答案】A 3.【答案】A 4.【答案】C
5.【答案】180°
解:因为∠COF=∠EOD,所以
∠AOE+∠DOB+∠COF=∠AOE+∠DOB+∠EOD=180°.
6.【答案】40°
解:因为∠BOD=40°,所以∠AOC=∠BOD=40°,因为OA平分∠COE,所以∠AOE=∠AOC=40°.21cnjy.com
7.解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3(等量代换).
因为∠2+∠4=180°(平角定义),
所以∠3+∠4=180°(等量代换).
8.解:由题图知,∠AOC与∠AOD互补,即∠AOC+∠AOD=180°,又∠AOC=∠AOD-80°,所以∠AOC+80°+∠AOC=180°,所以2∠AOC=100°,即∠AOC=50°,又因为∠AOC与∠BOD是对顶角,所以∠BOD=∠AOC=50°.因为OE平分∠BOD,所以∠BOE=∠BOD=25°,所以∠AOE=180°-∠BOE=180°-25°=155°.www.21-cn-jy.com
9.解:题图中的对顶角有:∠AOC与∠BOD,∠BOC与∠AOD,∠AOE与∠BOF,∠EOD与∠COF,∠EOB与∠AOF,∠EOC与∠DOF,共6对.
n条直线相交于一点,共有[2+4+6+8+…+2(n-1)]对对顶角.
而2=1×2,2+4=6=2×3,2+4+6=12=3×4,…,
故[2+4+6+8+…+2(n-1)]=(n-1)n=n2-n.
即n条直线相交于一点,共有(n2-n)对对顶角.
分析:本题为探究题,应从最简单的情况入手,观察对顶角对数增加的规律,从而解决问题.
