4.4.2 利用“内错角、同旁内角”判定平行线 同步练习
文档属性
| 名称 | 4.4.2 利用“内错角、同旁内角”判定平行线 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 431.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 15:40:46 | ||
图片预览


文档简介
4.4.2 利用“内错角、同旁内角”判定平行线
核心笔记: 1.平行线的判定方法2:内错角相等,两直线平行.
2.平行线的判定方法3:同旁内角互补,两直线平行.
基础训练
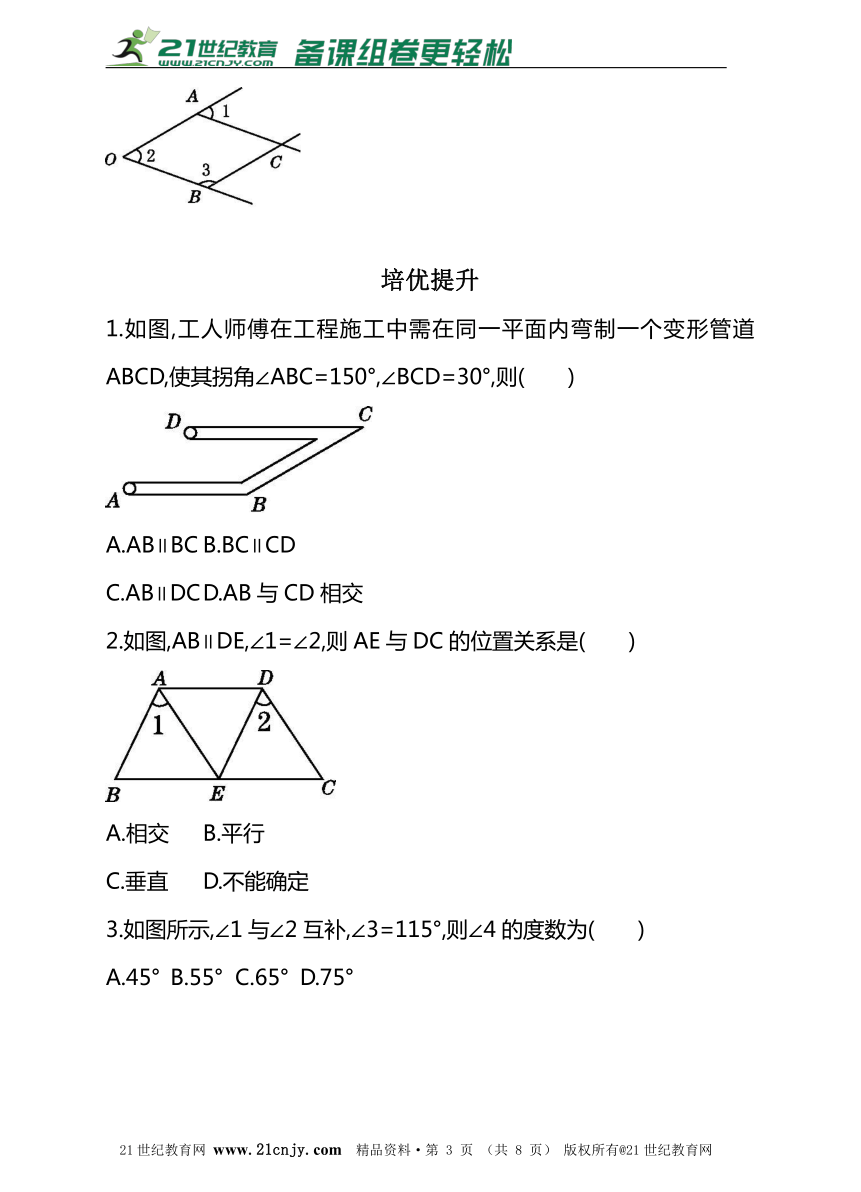
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,某住宅小区要修一条小路b与公路c的左侧相连,为保证小路b与已有小路a平行,测量得∠1=62°,则∠2的度数应是( )
A.28° B.82° C.118° D.128°
3.下列说法:①不相交且不重合的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交;⑤内错角相等,两直线平行;⑥同旁内角互补,两直线平行.其中正确的个数为( )21世纪教育网版权所有
A.1 B.2 C.3 D.4
4.如图所示,已知∠1+∠2=180°,那么__________∥_________.?
5.如图,根据平行线的判定填空:内错角相等,两直线平行.
如__________=__________,则FE ∥ HG.?
同旁内角互补,两直线平行.
如__________+__________=180°,则FE∥HG.?
6.如图,一条街道的两个拐角∠ABC与∠BCD均为140°,街道AB与CD平行吗?为什么?
7.如图是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21cnjy.com
培优提升
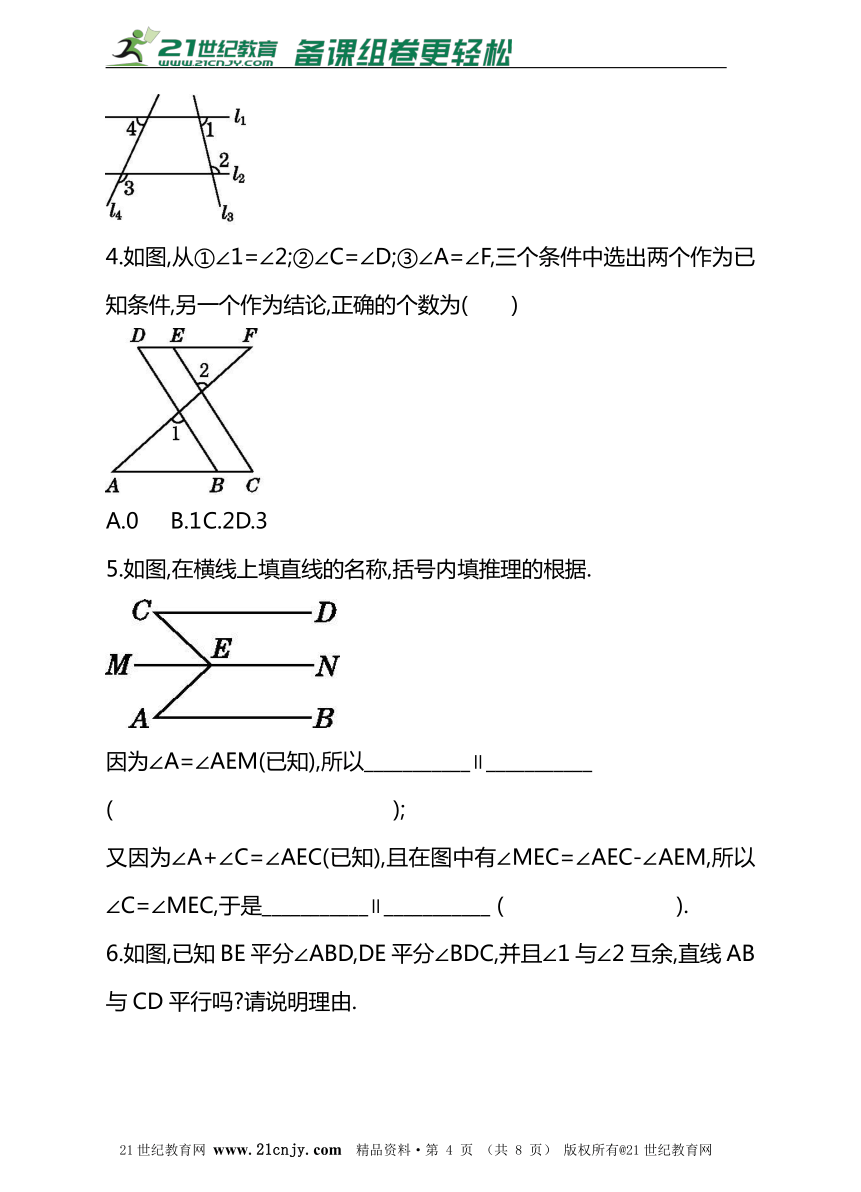
1.如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )21·cn·jy·com
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
2.如图,AB∥DE,∠1=∠2,则AE与DC的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
3.如图所示,∠1与∠2互补,∠3=115°,则∠4的度数为( )
A.45° B.55° C.65° D.75°
4.如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F,三个条件中选出两个作为已知条件,另一个作为结论,正确的个数为( )21教育网
A.0 B.1 C.2 D.3
5.如图,在横线上填直线的名称,括号内填推理的根据.
因为∠A=∠AEM(已知),所以___________∥___________
( );?
又因为∠A+∠C=∠AEC(已知),且在图中有∠MEC=∠AEC-∠AEM,所以∠C=∠MEC,于是___________∥___________ ( ).?
6.如图,已知BE平分∠ABD,DE平分∠BDC,并且∠1与∠2互余,直线AB与CD平行吗?请说明理由.www.21-cn-jy.com
7.如图:∠AHF+∠FMD=180°,HG平分∠AHM,MN平分∠DMH.
试说明:GH∥MN.
8.将一副三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°),当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值,并说明是哪组边互相平行.2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】B 2.【答案】C
3.【答案】C
解:①缺少前提条件:在同一平面内;②在同一平面内,两条直线的位置关系有三种:相交、平行、重合;③线段AB与CD没有交点,但是线段AB与CD所在的直线有可能有交点;④⑤⑥正确.故选C.【来源:21·世纪·教育·网】
4.【答案】AB;DC
5.【答案】∠FBC;∠BCG;∠FBC;∠BCH(答案不唯一)
6.解:平行,因为∠ABC=∠BCD=140°,所以AB∥CD(内错角相等,两直线平行).
7.解:OB∥AC,OA∥BC.理由如下:
因为∠1=50°,∠2=50°,
所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
【培优提升】
1.【答案】C
2.【答案】B
解:因为AB∥DE,所以∠1=∠AED,因为∠1=∠2,所以∠AED=∠2,所以AE∥DC.
3.【答案】C
4.【答案】D
解:直接利用平行线的判定与性质分别判断得出各结论均正确.
5.【答案】AB;MN;内错角相等,两直线平行;MN;CD;内错角相等,两直线平行
6.解:平行.理由:设∠ABE=∠4,∠CDE=∠3.因为BE平分∠ABD,DE平分∠BDC,所以∠2=∠4,∠1=∠3.又因为∠1与∠2互余(已知),所以∠1+∠2=90°,又因为∠1=∠3,∠2=∠4,所以∠3+∠4=90°(等量代换),所以∠1+∠3+∠2+∠4=180°,而∠1+∠3=∠BDC,∠2+∠4=∠ABD,所以∠BDC+∠ABD=180°,故AB∥CD(同旁内角互补,两直线平行).
7.解:因为∠AHF+∠FMD=180°,∠FMD=∠CME(对顶角相等),
所以∠AHF+∠CME=180°(等量代换).
所以AB∥CD(同旁内角互补,两直线平行).
所以∠AHF=∠DME(两直线平行,内错角相等).
因为HG平分∠AHM,MN平分∠DMH,
所以∠GHF=∠AHF,∠HMN=∠DME(角平分线定义).
所以∠GHF=∠HMN.
所以GH∥MN(内错角相等,两直线平行).
8.解:存在,
当∠ACE=30°时,AD∥BC,
当∠ACE=∠E=45°时,AC∥BE,
当∠ACE=120°时,AD∥CE,
当∠ACE=135°时,BE∥CD,
当∠ACE=165°时,BE∥AD.
核心笔记: 1.平行线的判定方法2:内错角相等,两直线平行.
2.平行线的判定方法3:同旁内角互补,两直线平行.
基础训练
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,某住宅小区要修一条小路b与公路c的左侧相连,为保证小路b与已有小路a平行,测量得∠1=62°,则∠2的度数应是( )
A.28° B.82° C.118° D.128°
3.下列说法:①不相交且不重合的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交;⑤内错角相等,两直线平行;⑥同旁内角互补,两直线平行.其中正确的个数为( )21世纪教育网版权所有
A.1 B.2 C.3 D.4
4.如图所示,已知∠1+∠2=180°,那么__________∥_________.?
5.如图,根据平行线的判定填空:内错角相等,两直线平行.
如__________=__________,则FE ∥ HG.?
同旁内角互补,两直线平行.
如__________+__________=180°,则FE∥HG.?
6.如图,一条街道的两个拐角∠ABC与∠BCD均为140°,街道AB与CD平行吗?为什么?
7.如图是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21cnjy.com
培优提升
1.如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )21·cn·jy·com
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
2.如图,AB∥DE,∠1=∠2,则AE与DC的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
3.如图所示,∠1与∠2互补,∠3=115°,则∠4的度数为( )
A.45° B.55° C.65° D.75°
4.如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F,三个条件中选出两个作为已知条件,另一个作为结论,正确的个数为( )21教育网
A.0 B.1 C.2 D.3
5.如图,在横线上填直线的名称,括号内填推理的根据.
因为∠A=∠AEM(已知),所以___________∥___________
( );?
又因为∠A+∠C=∠AEC(已知),且在图中有∠MEC=∠AEC-∠AEM,所以∠C=∠MEC,于是___________∥___________ ( ).?
6.如图,已知BE平分∠ABD,DE平分∠BDC,并且∠1与∠2互余,直线AB与CD平行吗?请说明理由.www.21-cn-jy.com
7.如图:∠AHF+∠FMD=180°,HG平分∠AHM,MN平分∠DMH.
试说明:GH∥MN.
8.将一副三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°),当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值,并说明是哪组边互相平行.2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】B 2.【答案】C
3.【答案】C
解:①缺少前提条件:在同一平面内;②在同一平面内,两条直线的位置关系有三种:相交、平行、重合;③线段AB与CD没有交点,但是线段AB与CD所在的直线有可能有交点;④⑤⑥正确.故选C.【来源:21·世纪·教育·网】
4.【答案】AB;DC
5.【答案】∠FBC;∠BCG;∠FBC;∠BCH(答案不唯一)
6.解:平行,因为∠ABC=∠BCD=140°,所以AB∥CD(内错角相等,两直线平行).
7.解:OB∥AC,OA∥BC.理由如下:
因为∠1=50°,∠2=50°,
所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
【培优提升】
1.【答案】C
2.【答案】B
解:因为AB∥DE,所以∠1=∠AED,因为∠1=∠2,所以∠AED=∠2,所以AE∥DC.
3.【答案】C
4.【答案】D
解:直接利用平行线的判定与性质分别判断得出各结论均正确.
5.【答案】AB;MN;内错角相等,两直线平行;MN;CD;内错角相等,两直线平行
6.解:平行.理由:设∠ABE=∠4,∠CDE=∠3.因为BE平分∠ABD,DE平分∠BDC,所以∠2=∠4,∠1=∠3.又因为∠1与∠2互余(已知),所以∠1+∠2=90°,又因为∠1=∠3,∠2=∠4,所以∠3+∠4=90°(等量代换),所以∠1+∠3+∠2+∠4=180°,而∠1+∠3=∠BDC,∠2+∠4=∠ABD,所以∠BDC+∠ABD=180°,故AB∥CD(同旁内角互补,两直线平行).
7.解:因为∠AHF+∠FMD=180°,∠FMD=∠CME(对顶角相等),
所以∠AHF+∠CME=180°(等量代换).
所以AB∥CD(同旁内角互补,两直线平行).
所以∠AHF=∠DME(两直线平行,内错角相等).
因为HG平分∠AHM,MN平分∠DMH,
所以∠GHF=∠AHF,∠HMN=∠DME(角平分线定义).
所以∠GHF=∠HMN.
所以GH∥MN(内错角相等,两直线平行).
8.解:存在,
当∠ACE=30°时,AD∥BC,
当∠ACE=∠E=45°时,AC∥BE,
当∠ACE=120°时,AD∥CE,
当∠ACE=135°时,BE∥CD,
当∠ACE=165°时,BE∥AD.
