4.6 两条平行线间的距离 同步练习
图片预览



文档简介
4.6 两条平行线间的距离
核心笔记: 1.公垂线、公垂线段的概念:与两条平行直线都垂直的直线,叫做这两条平行直线的公垂线,这时连接两个垂足的线段,叫做这两条平行直线的公垂线段.www.21-cn-jy.com
2.两条平行线的所有公垂线段都相等.
3.两条平行线的公垂线段的长度叫做两条平行线间的距离.
基础训练
1.如图,AB∥CD,EF⊥CD,MN,PQ都与AB,CD相交,则AB与CD的距离是( )
A.线段EF的长度 B.线段MN的长度
C.线段PQ的长度 D.无法确定
2.下列说法中,错误的是( )
A.平行线间的距离就是两条平行线间的公垂线
B.两平行线的所有公垂线段都相等
C.两点之间,线段最短
D.直线外一点到直线上各点连接的线段中,垂线段最短
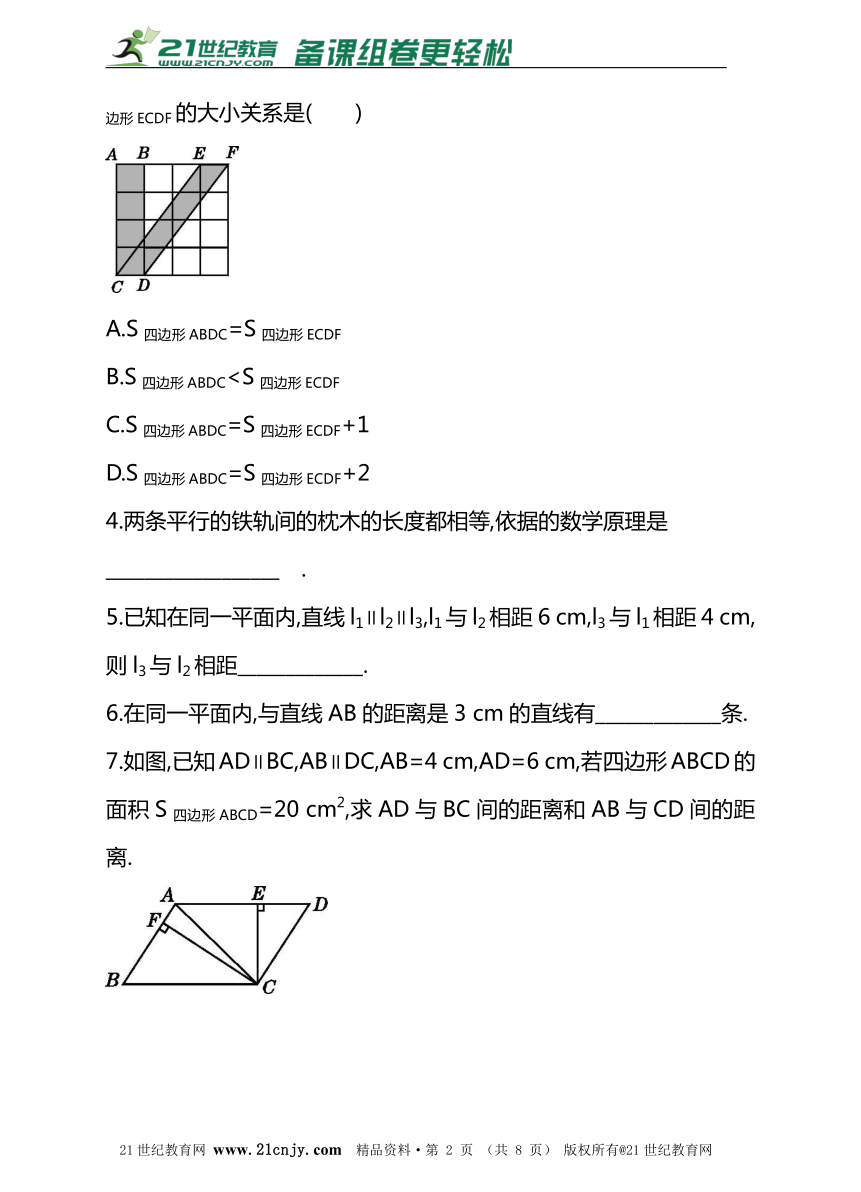
3.如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABDC与S四边形ECDF的大小关系是( )21cnjy.com
A.S四边形ABDC=S四边形ECDF
B.S四边形ABDCC.S四边形ABDC=S四边形ECDF+1
D.S四边形ABDC=S四边形ECDF+2
4.两条平行的铁轨间的枕木的长度都相等,依据的数学原理是
__________________ .?
5.已知在同一平面内,直线l1∥l2∥l3,l1与l2相距6 cm,l3与l1相距4 cm,则l3与l2相距_____________.?【来源:21·世纪·教育·网】
6.在同一平面内,与直线AB的距离是3 cm的直线有_____________条.?
7.如图,已知AD∥BC,AB∥DC,AB=4 cm,AD=6 cm,若四边形ABCD的面积S四边形ABCD=20 cm2,求AD与BC间的距离和AB与CD间的距离.
培优提升
1.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p,q,则称有序数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )2·1·c·n·j·y
A.2 B.3 C.4 D.5
2.如图,在一块平地上,雨后中间有一条积水沟,沟的两边是平行的,一只蚂蚁在A点,想过水沟来B点取食,几个学生在沟上沿与沟边垂直的方向放了四根小木棍,这只蚂蚁通过第( )号木棍,才能使从A到B的路径最短. 21·世纪*教育网
A. 1 B.2 C.3 D.4
3.如图所示,若a∥b,AB⊥b,CD⊥b,AB=4 cm,则CD=____________.?
4.如图为某大楼一、二楼间的楼梯台阶示意图,共20阶台阶,每阶台阶的高度均为a cm,宽度均为b cm(a≠b).求图中一楼地面与二楼地面的距离为cm.www-2-1-cnjy-com
5.如图,已知直线AD∥BC,三角形ABC的面积为6,线段DC=3,则点B到CD的距离是 .?21*cnjy*com
6.如图,在长方形ABCD中,AB=6 cm,长方形的面积为24 cm2.求AB与CD之间的距离.
7.如图,已知直线l1∥l2∥l3∥l4∥l5,若l1与l5的距离为8 cm,且l1与l2的距离、l2与l3的距离、l3与l4的距离、l4与l5的距离依次增加1 cm,求l1与l2的距离.21·cn·jy·com
8.如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E和点F,H,G分别在直线AD和BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是否是两条平行线AD,BC之间的距离?请说明理由.2-1-c-n-j-y
参考答案
【基础训练】
1.【答案】A 2.【答案】A
3.【答案】A
解:S四边形ABDC=CD·AC=1×4=4,S四边形ECDF=CD·AC=1×4=4,故选A.
4.【答案】两条平行线的所有公垂线段都相等
5.【答案】2 cm或10 cm
解:分两种情况讨论:①如图①所示,l3与l2相距2 cm;②如图②所示,l3与l2相距10 cm.
①
②
6.【答案】2
7.解:由题知,AD与BC间的距离为CE的长度,AB与CD间的距离为CF的长度.
S四边形ABCD=2S三角形ABC=2×AB·CF=2××4·CF=20,解得CF=5(cm).
S四边形ABCD=2S三角形ADC=2×AD·CE=2××6·CE=20,解得CE=(cm).
故AD与BC间的距离为cm,AB与CD间的距离为5 cm.
【培优提升】
1.【答案】C
解:如图,因为到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1,b2上,所以“距离坐标”是(1,2)的点是M1,M2,M3,M4,一共4个.21世纪教育网版权所有
2.【答案】B 3.【答案】4 cm
4.【答案】20a
解:因为一楼地面与二楼地面的距离=全部台阶的高度总和,所以一楼地面与二楼地面的距离为:a×20=20a(cm).21教育网
5.【答案】4
解:因为AD∥BC,所以三角形BCD的面积=三角形ABC的面积=6,所以点B到CD的距离为=4.
6.解:由题意知,AD的长即为AB与CD之间的距离,AD=S长方形
÷AB=24÷6=4(cm)
故AB与CD之间的距离为4 cm.
7.解:如图所示,在l1上取一点A,过点A作AE⊥l5分别交l2,l3,l4,l5于点B,C,D,E,则线段AB,BC,CD,DE的长分别为l1与l2,l2与l3,l3与l4,l4与l5的距离.设AB=x cm,则BC=(x+1) cm,CD=(x+1)+1=(x+2)cm,DE=(x+2)+1=(x+3)cm,于是可列方程:x+(x+1)+(x+2)+(x+3)=8,解得x=0.5.所以l1与l2的距离为0.5 cm.
8.解:是.理由如下:
因为AB∥EF,所以∠A=∠FED=110°,
因为CD∥EG,所以∠D=∠AEG=110°,
所以∠FED=∠AEG,
又因为∠FED=∠FEG+∠DEG,
∠AEG=∠FEG+∠AEF,
所以∠DEG=∠AEF,
因为EH平分∠FEG,
所以∠FEH=∠GEH,
所以∠FEH+∠AEF=∠GEH+∠DEG,
即∠AEH=∠DEH,
而∠AEH+∠DEH=180°,
所以∠AEH=∠DEH=90°,
所以EH⊥AD,即EH的长是两条平行线AD,BC之间的距离.
核心笔记: 1.公垂线、公垂线段的概念:与两条平行直线都垂直的直线,叫做这两条平行直线的公垂线,这时连接两个垂足的线段,叫做这两条平行直线的公垂线段.www.21-cn-jy.com
2.两条平行线的所有公垂线段都相等.
3.两条平行线的公垂线段的长度叫做两条平行线间的距离.
基础训练
1.如图,AB∥CD,EF⊥CD,MN,PQ都与AB,CD相交,则AB与CD的距离是( )
A.线段EF的长度 B.线段MN的长度
C.线段PQ的长度 D.无法确定
2.下列说法中,错误的是( )
A.平行线间的距离就是两条平行线间的公垂线
B.两平行线的所有公垂线段都相等
C.两点之间,线段最短
D.直线外一点到直线上各点连接的线段中,垂线段最短
3.如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABDC与S四边形ECDF的大小关系是( )21cnjy.com
A.S四边形ABDC=S四边形ECDF
B.S四边形ABDC
D.S四边形ABDC=S四边形ECDF+2
4.两条平行的铁轨间的枕木的长度都相等,依据的数学原理是
__________________ .?
5.已知在同一平面内,直线l1∥l2∥l3,l1与l2相距6 cm,l3与l1相距4 cm,则l3与l2相距_____________.?【来源:21·世纪·教育·网】
6.在同一平面内,与直线AB的距离是3 cm的直线有_____________条.?
7.如图,已知AD∥BC,AB∥DC,AB=4 cm,AD=6 cm,若四边形ABCD的面积S四边形ABCD=20 cm2,求AD与BC间的距离和AB与CD间的距离.
培优提升
1.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p,q,则称有序数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )2·1·c·n·j·y
A.2 B.3 C.4 D.5
2.如图,在一块平地上,雨后中间有一条积水沟,沟的两边是平行的,一只蚂蚁在A点,想过水沟来B点取食,几个学生在沟上沿与沟边垂直的方向放了四根小木棍,这只蚂蚁通过第( )号木棍,才能使从A到B的路径最短. 21·世纪*教育网
A. 1 B.2 C.3 D.4
3.如图所示,若a∥b,AB⊥b,CD⊥b,AB=4 cm,则CD=____________.?
4.如图为某大楼一、二楼间的楼梯台阶示意图,共20阶台阶,每阶台阶的高度均为a cm,宽度均为b cm(a≠b).求图中一楼地面与二楼地面的距离为cm.www-2-1-cnjy-com
5.如图,已知直线AD∥BC,三角形ABC的面积为6,线段DC=3,则点B到CD的距离是 .?21*cnjy*com
6.如图,在长方形ABCD中,AB=6 cm,长方形的面积为24 cm2.求AB与CD之间的距离.
7.如图,已知直线l1∥l2∥l3∥l4∥l5,若l1与l5的距离为8 cm,且l1与l2的距离、l2与l3的距离、l3与l4的距离、l4与l5的距离依次增加1 cm,求l1与l2的距离.21·cn·jy·com
8.如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E和点F,H,G分别在直线AD和BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是否是两条平行线AD,BC之间的距离?请说明理由.2-1-c-n-j-y
参考答案
【基础训练】
1.【答案】A 2.【答案】A
3.【答案】A
解:S四边形ABDC=CD·AC=1×4=4,S四边形ECDF=CD·AC=1×4=4,故选A.
4.【答案】两条平行线的所有公垂线段都相等
5.【答案】2 cm或10 cm
解:分两种情况讨论:①如图①所示,l3与l2相距2 cm;②如图②所示,l3与l2相距10 cm.
①
②
6.【答案】2
7.解:由题知,AD与BC间的距离为CE的长度,AB与CD间的距离为CF的长度.
S四边形ABCD=2S三角形ABC=2×AB·CF=2××4·CF=20,解得CF=5(cm).
S四边形ABCD=2S三角形ADC=2×AD·CE=2××6·CE=20,解得CE=(cm).
故AD与BC间的距离为cm,AB与CD间的距离为5 cm.
【培优提升】
1.【答案】C
解:如图,因为到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1,b2上,所以“距离坐标”是(1,2)的点是M1,M2,M3,M4,一共4个.21世纪教育网版权所有
2.【答案】B 3.【答案】4 cm
4.【答案】20a
解:因为一楼地面与二楼地面的距离=全部台阶的高度总和,所以一楼地面与二楼地面的距离为:a×20=20a(cm).21教育网
5.【答案】4
解:因为AD∥BC,所以三角形BCD的面积=三角形ABC的面积=6,所以点B到CD的距离为=4.
6.解:由题意知,AD的长即为AB与CD之间的距离,AD=S长方形
÷AB=24÷6=4(cm)
故AB与CD之间的距离为4 cm.
7.解:如图所示,在l1上取一点A,过点A作AE⊥l5分别交l2,l3,l4,l5于点B,C,D,E,则线段AB,BC,CD,DE的长分别为l1与l2,l2与l3,l3与l4,l4与l5的距离.设AB=x cm,则BC=(x+1) cm,CD=(x+1)+1=(x+2)cm,DE=(x+2)+1=(x+3)cm,于是可列方程:x+(x+1)+(x+2)+(x+3)=8,解得x=0.5.所以l1与l2的距离为0.5 cm.
8.解:是.理由如下:
因为AB∥EF,所以∠A=∠FED=110°,
因为CD∥EG,所以∠D=∠AEG=110°,
所以∠FED=∠AEG,
又因为∠FED=∠FEG+∠DEG,
∠AEG=∠FEG+∠AEF,
所以∠DEG=∠AEF,
因为EH平分∠FEG,
所以∠FEH=∠GEH,
所以∠FEH+∠AEF=∠GEH+∠DEG,
即∠AEH=∠DEH,
而∠AEH+∠DEH=180°,
所以∠AEH=∠DEH=90°,
所以EH⊥AD,即EH的长是两条平行线AD,BC之间的距离.
