2017年中考数学二轮专题复习讲义--第5讲图表信息问题
文档属性
| 名称 | 2017年中考数学二轮专题复习讲义--第5讲图表信息问题 |  | |
| 格式 | zip | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-24 09:29:38 | ||
图片预览



文档简介
2017年中考数学二轮专题复习讲义(5)图表信息问题
【专题点拨】
图表信息题关键是“识图”和“用图”,主要是通过图形及表格信息,考查学生收集信息和处理信息的能力.解题时,要充分审视图形、表格,全面掌握其提供的信息,理解其实质,把握其方法规律,从而解决问题。21·世纪*教育网
【解题策略】
抓住图形或表格中的关键数据,筛选出有价值的信息,利用数据反映出的信息、规律、性质等建立数学模型解决。
【典例解析】
类型一:图像信息题
例题1:.(2016广东省贺州市第10题)抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为( )21*cnjy*com
A. B. C. D.
【答案】B
【解析】(1)、二次函数的图象;(2)、一次函数的图象;(3)、反比例函数的图象
【解答】根据二次函数图象与系数的关系确定a>0,b<0,c<0,根据一次函数和反比例函数的性质确定答案.由抛物线可知,a>0,b<0,c<0,∴一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=的图象在第二、四象限,
变式训练1:
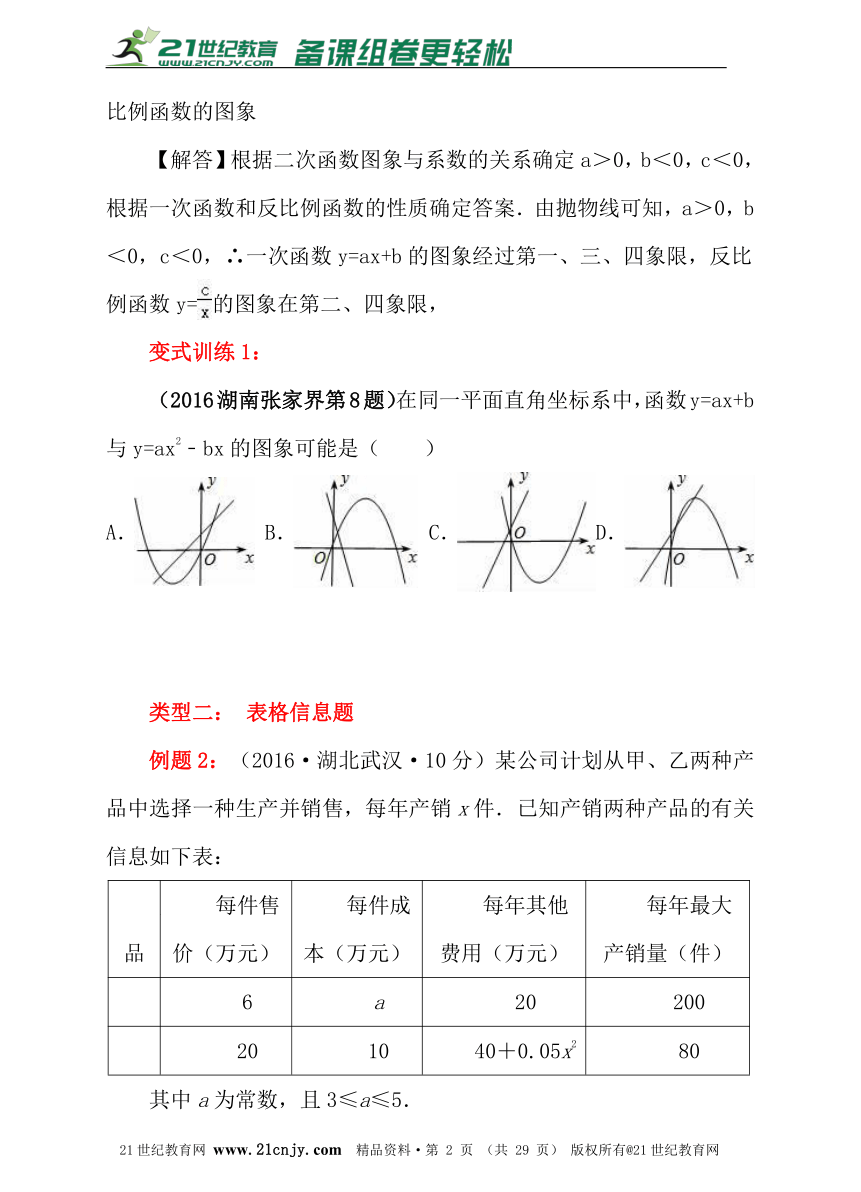
(2016湖南张家界第8题)在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A. B. C.D.
类型二: 表格信息题
例题2:(2016·湖北武汉·10分)某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:
产品
每件售价(万元)
每件成本(万元)
每年其他费用(万元)
每年最大产销量(件)
甲
6
a
20
200
乙
20
10
40+0.05x2
80
其中a为常数,且3≤a≤5.
(1) 若产销甲、 乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【考点】二次函数的应用,一次函数的应用
【答案】 (1)y1=(6-a)x-20(0<x≤200),y2=-0.05x2+10x-40(0<x≤80);(2) 产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)当3≤a<3.7时,选择甲产品;当a=3.7时,选择甲乙产品;当3.7<a≤5时,选择乙产品
【解析】解:(1) y1=(6-a)x-20(0<x≤200),y2=-0.05x2+10x-40(0<x≤80);
(2)甲产品:∵3≤a≤5,∴6-a>0,∴y1随x的增大而增大.
∴当x=200时,y1max=1180-200a(3≤a≤5)
乙产品:y2=-0.05x2+10x-40(0<x≤80)
∴当0<x≤80时,y2随x的增大而增大.
当x=80时,y2max=440(万元).
∴产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)1180-200>440,解得3≤a<3.7时,此时选择甲产品;
1180-200=440,解得a=3.7时,此时选择甲乙产品;
1180-200<440,解得3.7<a≤5时,此时选择乙产品.
∴当3≤a<3.7时,生产甲产品的利润高;
当a=3.7时,生产甲乙两种产品的利润相同;
当3.7<a≤5时,上产乙产品的利润高.
变式训练2:
(2016·四川眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
类型三: 图文信息题
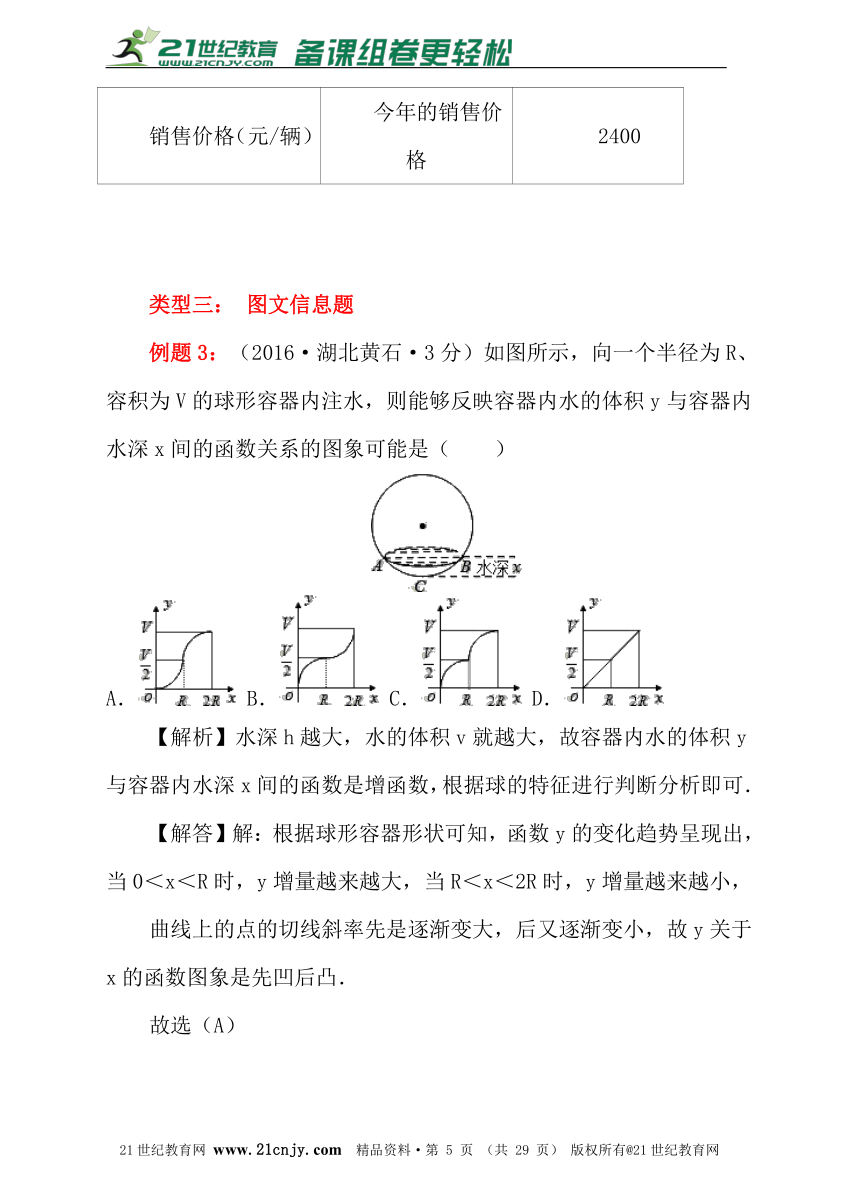
例题3:(2016·湖北黄石·3分)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )www.21-cn-jy.com
A. B. C. D.
【解析】水深h越大,水的体积v就越大,故容器内水的体积y与容器内水深x间的函数是增函数,根据球的特征进行判断分析即可.
【解答】解:根据球形容器形状可知,函数y的变化趋势呈现出,当0<x<R时,y增量越来越大,当R<x<2R时,y增量越来越小,
曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,故y关于x的函数图象是先凹后凸.
故选(A)
【点评】本题主要考查了函数图象的变化特征,解题的关键是利用数形结合的数学思想方法.解得此类试题时注意,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.21*cnjy*com
变式训练3:
(2016·黑龙江龙东·3分)如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
A. B. C. D.
类型四: 综合创新类信息题
例题4:(2016·湖北随州·9分)九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
【解析】二次函数的应用;一元一次不等式的应用.(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50<x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,套入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当0≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50<x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
【解答】解:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b(k、b为常数且k≠0),
∵y=kx+b经过点(0,40)、(50,90),
∴,解得:,
∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90.
∴售价y与时间x的函数关系式为y=.
由书记可知每天的销售量p与时间x成一次函数关系,
设每天的销售量p与时间x的函数关系式为p=mx+n(m、n为常数,且m≠0),
∵p=mx+n过点(60,80)、(30,140),
∴,解得:,
∴p=﹣2x+200(0≤x≤90,且x为整数),
当0≤x≤50时,w=(y﹣30)?p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;21教育网
当50<x≤90时,w=(90﹣30)(﹣2x+200)=﹣120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是
w=.
(2)当0≤x≤50时,w=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,
∵a=﹣2<0且0≤x≤50,
∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,w=﹣120x+12000,
∵k=﹣120<0,w随x增大而减小,
∴当x=50时,w取最大值,最大值为6000元.
∵6050>6000,
∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当0≤x≤50时,令w=﹣2x2+180x+2000≥5600,即﹣2x2+180x﹣3600≥0,
解得:30≤x≤50,
50﹣30+1=21(天);
当50<x≤90时,令w=﹣120x+12000≥5600,即﹣120x+6400≥0,
解得:50<x≤53,
∵x为整数,
∴50<x≤53,
53﹣50=3(天).
综上可知:21+3=24(天),
故该商品在销售过程中,共有24天每天的销售利润不低于5600元.
变式训练4:
(2016·四川南充)已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=?请说明理由.
【能力检测】
1. (2016广西南宁3分)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
2. (2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
3. (2016·山东省德州市·4分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:21世纪教育网版权所有
第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
4. (2016·浙江省绍兴市·10分)课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
5. (2016·重庆市B卷·12分)如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.21cnjy.com
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y=x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.www-2-1-cnjy-com
【参考答案】
变式训练1:
(2016湖南张家界第8题)在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )【来源:21·世纪·教育·网】
A. B. C.D.
【答案】C.
【解析】考点:1一次函数图像;2二次函数图像.
【解答】:选项A:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误;选项B:一次函数图像经过一、二、四象限,因此a<0,b>0,对于二次函数y=ax2﹣bx图像应该开口向下,对称轴在y轴左侧,不合题意,此选项错误;2-1-c-n-j-y
选项C:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,符合题意,此选项正确;选项D:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误.故选C.【出处:21教育名师】
变式训练2:
(2016·四川眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.【版权所有:21教育】
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?21教育名师原创作品
A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
【解析】(1)设去年A型车每辆x元,那么今年每辆(x+400)元,列出方程即可解决问题.
(2)设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.
【解答】解:(1)设去年A型车每辆x元,那么今年每辆(x+400)元,
根据题意得,
解之得x=1600,
经检验,x=1600是方程的解.
答:今年A型车每辆2000元.
(2)设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,
根据题意得50﹣m≤2m
解之得m≥,
∵y=(2000﹣1100)m+(2400﹣1400)(50﹣m)=﹣100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆.
【点评】不同考查一次函数的应用、分式方程等知识,解题的关键是设未知数列出方程解决问题,注意分式方程必须检验,学会构建一次函数,利用一次函数性质解决实际问题中的最值问题,属于中考常考题型.
变式训练3:
(2016·黑龙江龙东·3分)如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
A. B. C. D.
【解析】动点问题的函数图象.根据直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形可知,当0≤t≤时,以及当<t≤2时,当2<t≤3时,求出函数关系式,即可得出答案.
【解答】解:∵直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s,
∴s关于t的函数大致图象应为:三角形进入正方形以前s增大,
当0≤t≤时,s=×1×1+2×2﹣=﹣t2;
当<t≤2时,s=×12=;
当2<t≤3时,s=﹣(3﹣t)2=t2﹣3t,
∴A符合要求,故选A.
变式训练4:
(2016·四川南充)已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=?请说明理由.
【分析】(1)由△PBC∽△PAM,推出∠PAM=∠PBC,由∠PBC+∠PBA=90°,推出∠PAM+∠PBA=90°即可证明AP⊥BN,由△PBC∽△PAM,推出==,由△BAP∽△BNA,推出=,得到=,由此即可证明.
(2)①结论仍然成立,证明方法类似(1).②这样的点P不存在.利用反证法证明.假设PC=,推出矛盾即可.
【解答】(1)证明:如图一中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC, ==,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴=,
∴=,
∵AB=BC,
∴AN=AM.
(2)解:①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC, ==,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴=,
∴=,
∵AB=BC,
∴AN=AM.
②这样的点P不存在.
理由:假设PC=,
如图三中,以点C为圆心为半径画圆,以AB为直径画圆,
CO==>1+,
∴两个圆外离,∴∠APB<90°,这与AP⊥PB矛盾,
∴假设不可能成立,
∴满足PC=的点P不存在.
【点评】本题考查相似三角形综合题、正方形的性质、圆的有关知识,解题的关键是熟练应用相似三角形性质解决问题,最后一个问题利用圆的位置关系解决问题,有一定难度,属于中考压轴题.
【能力检测】
1. (2016广西南宁3分)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
【解析】函数的概念.根据函数的意义求解即可求出答案.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,故D正确.
故选D.
【点评】主要考查了函数的定义.注意函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.21·cn·jy·com
2. (2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
【解析】动点问题的函数图象.△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
3. (2016·山东省德州市·4分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
【解析】一次函数的应用.(1)由表中数据得出xy=6000,即可得出结果;
(2)由题意得出方程,解方程即可,注意检验.
【解答】解:(1)由表中数据得:xy=6000,
∴y=,
∴y是x的反比例函数,
故所求函数关系式为y=;
(2)由题意得:(x﹣120)y=3000,
把y=代入得:(x﹣120)?=3000,
解得:x=240;
经检验,x=240是原方程的根;
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
【点评】本题考查了反比例函数的应用、列分式方程解应用题;根据题意得出函数关系式和列出方程是解决问题的关键.
4. (2016·浙江省绍兴市·10分)课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
【分析】二次函数的应用.(1)根据矩形和正方形的周长进行解答即可;
(2)设AB为xcm,利用二次函数的最值解答即可.
【解答】解:(1)由已知可得:AD=,
则S=1×m2,
(2)设AB=xm,则AD=3﹣m,
∵,
∴,
设窗户面积为S,由已知得:
,
当x=m时,且x=m在的范围内,,
∴与课本中的例题比较,现在窗户透光面积的最大值变大.
5. (2016·重庆市B卷·12分)如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.【来源:21cnj*y.co*m】
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y=x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
【解析】二次函数综合题.(1)根据S△AMO:S四边形AONB=1:48,求出三角形相似的相似比为1:7,从而求出BN,继而求出点B的坐标,用待定系数法求出直线解析式.
(2)先判断出PE×PF最大时,PE×PD也最大,再求出PE×PF最大时G(5,),再简单的计算即可;
(3)由平移的特点及坐标系中,两点间的距离公式得A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,最后分三种情况计算即可.
【解答】解:(1)∵点C是二次函数y=x2﹣2x+1图象的顶点,
∴C(2,﹣1),
∵PE⊥x轴,BN⊥x轴,
∴△MAO∽△MBN,
∵S△AMO:S四边形AONB=1:48,
∴S△AMO:S△BMN=1:49,
∴OA:BN=1:7,
∵OA=1
∴BN=7,
把y=7代入二次函数解析式y=x2﹣2x+1中,可得7=x2﹣2x+1,
∴x1=﹣2(舍),x2=6
∴B(6,7),
∵A的坐标为(0,1),
∴直线AB解析式为y=x+1,
∵C(2,﹣1),B(6,7),
∴直线BC解析式为y=2x﹣5.
(2)如图1,
设点P(x0,x0+1),
∴D(,x0+1),
∴PE=x0+1,PD=3﹣x0,
∵△PDF∽△BGN,
∴PF:PD的值固定,
∴PE×PF最大时,PE×PD也最大,
PE×PD=(x0+1)(3﹣x0)=﹣x02+x0+3,
∴当x0=时,PE×PD最大,
即:PE×PF最大.此时G(5,)
∵△MNB是等腰直角三角形,
过B作x轴的平行线,
∴BH=B1H,
GH+BH的最小值转化为求GH+HB1的最小值,
∴当GH和HB1在一条直线上时,GH+HB1的值最小,
此时H(5,6),最小值为7﹣=
(3)令直线BC与x轴交于点I,
∴I(,0)
∴IN=,IN:BN=1:2,
∴沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A′(m,1+2m),C′(2+m,﹣1+2m),2·1·c·n·j·y
∴A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,
当∠A′KC′=90°时,A′K2+KC′2=A′C′2,解得m=,此时t=m=2±;
当∠KC′A′=90°时,KC′2+A′C′2=A′K2,解得m=4,此时t=m=4;
当∠KA′C′=90°时,A′C′2+A′K2=KC′2,解得m=0,此时t=0.
【点评】此题是二次函数综合题,主要考查了相似三角形的性质,待定系数法求函数解析式,两点间的结论公式,解本题的关键是相似三角形的性质的运用.
【专题点拨】
图表信息题关键是“识图”和“用图”,主要是通过图形及表格信息,考查学生收集信息和处理信息的能力.解题时,要充分审视图形、表格,全面掌握其提供的信息,理解其实质,把握其方法规律,从而解决问题。21·世纪*教育网
【解题策略】
抓住图形或表格中的关键数据,筛选出有价值的信息,利用数据反映出的信息、规律、性质等建立数学模型解决。
【典例解析】
类型一:图像信息题
例题1:.(2016广东省贺州市第10题)抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为( )21*cnjy*com
A. B. C. D.
【答案】B
【解析】(1)、二次函数的图象;(2)、一次函数的图象;(3)、反比例函数的图象
【解答】根据二次函数图象与系数的关系确定a>0,b<0,c<0,根据一次函数和反比例函数的性质确定答案.由抛物线可知,a>0,b<0,c<0,∴一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=的图象在第二、四象限,
变式训练1:
(2016湖南张家界第8题)在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A. B. C.D.
类型二: 表格信息题
例题2:(2016·湖北武汉·10分)某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:
产品
每件售价(万元)
每件成本(万元)
每年其他费用(万元)
每年最大产销量(件)
甲
6
a
20
200
乙
20
10
40+0.05x2
80
其中a为常数,且3≤a≤5.
(1) 若产销甲、 乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【考点】二次函数的应用,一次函数的应用
【答案】 (1)y1=(6-a)x-20(0<x≤200),y2=-0.05x2+10x-40(0<x≤80);(2) 产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)当3≤a<3.7时,选择甲产品;当a=3.7时,选择甲乙产品;当3.7<a≤5时,选择乙产品
【解析】解:(1) y1=(6-a)x-20(0<x≤200),y2=-0.05x2+10x-40(0<x≤80);
(2)甲产品:∵3≤a≤5,∴6-a>0,∴y1随x的增大而增大.
∴当x=200时,y1max=1180-200a(3≤a≤5)
乙产品:y2=-0.05x2+10x-40(0<x≤80)
∴当0<x≤80时,y2随x的增大而增大.
当x=80时,y2max=440(万元).
∴产销甲种产品的最大年利润为(1180-200a)万元,产销乙种产品的最大年利润为440万元;(3)1180-200>440,解得3≤a<3.7时,此时选择甲产品;
1180-200=440,解得a=3.7时,此时选择甲乙产品;
1180-200<440,解得3.7<a≤5时,此时选择乙产品.
∴当3≤a<3.7时,生产甲产品的利润高;
当a=3.7时,生产甲乙两种产品的利润相同;
当3.7<a≤5时,上产乙产品的利润高.
变式训练2:
(2016·四川眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
类型三: 图文信息题
例题3:(2016·湖北黄石·3分)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )www.21-cn-jy.com
A. B. C. D.
【解析】水深h越大,水的体积v就越大,故容器内水的体积y与容器内水深x间的函数是增函数,根据球的特征进行判断分析即可.
【解答】解:根据球形容器形状可知,函数y的变化趋势呈现出,当0<x<R时,y增量越来越大,当R<x<2R时,y增量越来越小,
曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,故y关于x的函数图象是先凹后凸.
故选(A)
【点评】本题主要考查了函数图象的变化特征,解题的关键是利用数形结合的数学思想方法.解得此类试题时注意,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.21*cnjy*com
变式训练3:
(2016·黑龙江龙东·3分)如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
A. B. C. D.
类型四: 综合创新类信息题
例题4:(2016·湖北随州·9分)九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
【解析】二次函数的应用;一元一次不等式的应用.(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50<x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,套入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当0≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50<x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
【解答】解:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b(k、b为常数且k≠0),
∵y=kx+b经过点(0,40)、(50,90),
∴,解得:,
∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90.
∴售价y与时间x的函数关系式为y=.
由书记可知每天的销售量p与时间x成一次函数关系,
设每天的销售量p与时间x的函数关系式为p=mx+n(m、n为常数,且m≠0),
∵p=mx+n过点(60,80)、(30,140),
∴,解得:,
∴p=﹣2x+200(0≤x≤90,且x为整数),
当0≤x≤50时,w=(y﹣30)?p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;21教育网
当50<x≤90时,w=(90﹣30)(﹣2x+200)=﹣120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是
w=.
(2)当0≤x≤50时,w=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,
∵a=﹣2<0且0≤x≤50,
∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,w=﹣120x+12000,
∵k=﹣120<0,w随x增大而减小,
∴当x=50时,w取最大值,最大值为6000元.
∵6050>6000,
∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当0≤x≤50时,令w=﹣2x2+180x+2000≥5600,即﹣2x2+180x﹣3600≥0,
解得:30≤x≤50,
50﹣30+1=21(天);
当50<x≤90时,令w=﹣120x+12000≥5600,即﹣120x+6400≥0,
解得:50<x≤53,
∵x为整数,
∴50<x≤53,
53﹣50=3(天).
综上可知:21+3=24(天),
故该商品在销售过程中,共有24天每天的销售利润不低于5600元.
变式训练4:
(2016·四川南充)已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=?请说明理由.
【能力检测】
1. (2016广西南宁3分)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
2. (2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
3. (2016·山东省德州市·4分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:21世纪教育网版权所有
第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
4. (2016·浙江省绍兴市·10分)课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
5. (2016·重庆市B卷·12分)如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.21cnjy.com
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y=x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.www-2-1-cnjy-com
【参考答案】
变式训练1:
(2016湖南张家界第8题)在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )【来源:21·世纪·教育·网】
A. B. C.D.
【答案】C.
【解析】考点:1一次函数图像;2二次函数图像.
【解答】:选项A:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误;选项B:一次函数图像经过一、二、四象限,因此a<0,b>0,对于二次函数y=ax2﹣bx图像应该开口向下,对称轴在y轴左侧,不合题意,此选项错误;2-1-c-n-j-y
选项C:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,符合题意,此选项正确;选项D:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误.故选C.【出处:21教育名师】
变式训练2:
(2016·四川眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.【版权所有:21教育】
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?21教育名师原创作品
A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
【解析】(1)设去年A型车每辆x元,那么今年每辆(x+400)元,列出方程即可解决问题.
(2)设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.
【解答】解:(1)设去年A型车每辆x元,那么今年每辆(x+400)元,
根据题意得,
解之得x=1600,
经检验,x=1600是方程的解.
答:今年A型车每辆2000元.
(2)设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,
根据题意得50﹣m≤2m
解之得m≥,
∵y=(2000﹣1100)m+(2400﹣1400)(50﹣m)=﹣100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆.
【点评】不同考查一次函数的应用、分式方程等知识,解题的关键是设未知数列出方程解决问题,注意分式方程必须检验,学会构建一次函数,利用一次函数性质解决实际问题中的最值问题,属于中考常考题型.
变式训练3:
(2016·黑龙江龙东·3分)如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
A. B. C. D.
【解析】动点问题的函数图象.根据直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形可知,当0≤t≤时,以及当<t≤2时,当2<t≤3时,求出函数关系式,即可得出答案.
【解答】解:∵直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s,
∴s关于t的函数大致图象应为:三角形进入正方形以前s增大,
当0≤t≤时,s=×1×1+2×2﹣=﹣t2;
当<t≤2时,s=×12=;
当2<t≤3时,s=﹣(3﹣t)2=t2﹣3t,
∴A符合要求,故选A.
变式训练4:
(2016·四川南充)已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=?请说明理由.
【分析】(1)由△PBC∽△PAM,推出∠PAM=∠PBC,由∠PBC+∠PBA=90°,推出∠PAM+∠PBA=90°即可证明AP⊥BN,由△PBC∽△PAM,推出==,由△BAP∽△BNA,推出=,得到=,由此即可证明.
(2)①结论仍然成立,证明方法类似(1).②这样的点P不存在.利用反证法证明.假设PC=,推出矛盾即可.
【解答】(1)证明:如图一中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC, ==,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴=,
∴=,
∵AB=BC,
∴AN=AM.
(2)解:①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC, ==,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴=,
∴=,
∵AB=BC,
∴AN=AM.
②这样的点P不存在.
理由:假设PC=,
如图三中,以点C为圆心为半径画圆,以AB为直径画圆,
CO==>1+,
∴两个圆外离,∴∠APB<90°,这与AP⊥PB矛盾,
∴假设不可能成立,
∴满足PC=的点P不存在.
【点评】本题考查相似三角形综合题、正方形的性质、圆的有关知识,解题的关键是熟练应用相似三角形性质解决问题,最后一个问题利用圆的位置关系解决问题,有一定难度,属于中考压轴题.
【能力检测】
1. (2016广西南宁3分)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
【解析】函数的概念.根据函数的意义求解即可求出答案.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,故D正确.
故选D.
【点评】主要考查了函数的定义.注意函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.21·cn·jy·com
2. (2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
【解析】动点问题的函数图象.△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
3. (2016·山东省德州市·4分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
【解析】一次函数的应用.(1)由表中数据得出xy=6000,即可得出结果;
(2)由题意得出方程,解方程即可,注意检验.
【解答】解:(1)由表中数据得:xy=6000,
∴y=,
∴y是x的反比例函数,
故所求函数关系式为y=;
(2)由题意得:(x﹣120)y=3000,
把y=代入得:(x﹣120)?=3000,
解得:x=240;
经检验,x=240是原方程的根;
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
【点评】本题考查了反比例函数的应用、列分式方程解应用题;根据题意得出函数关系式和列出方程是解决问题的关键.
4. (2016·浙江省绍兴市·10分)课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
【分析】二次函数的应用.(1)根据矩形和正方形的周长进行解答即可;
(2)设AB为xcm,利用二次函数的最值解答即可.
【解答】解:(1)由已知可得:AD=,
则S=1×m2,
(2)设AB=xm,则AD=3﹣m,
∵,
∴,
设窗户面积为S,由已知得:
,
当x=m时,且x=m在的范围内,,
∴与课本中的例题比较,现在窗户透光面积的最大值变大.
5. (2016·重庆市B卷·12分)如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.【来源:21cnj*y.co*m】
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y=x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
【解析】二次函数综合题.(1)根据S△AMO:S四边形AONB=1:48,求出三角形相似的相似比为1:7,从而求出BN,继而求出点B的坐标,用待定系数法求出直线解析式.
(2)先判断出PE×PF最大时,PE×PD也最大,再求出PE×PF最大时G(5,),再简单的计算即可;
(3)由平移的特点及坐标系中,两点间的距离公式得A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,最后分三种情况计算即可.
【解答】解:(1)∵点C是二次函数y=x2﹣2x+1图象的顶点,
∴C(2,﹣1),
∵PE⊥x轴,BN⊥x轴,
∴△MAO∽△MBN,
∵S△AMO:S四边形AONB=1:48,
∴S△AMO:S△BMN=1:49,
∴OA:BN=1:7,
∵OA=1
∴BN=7,
把y=7代入二次函数解析式y=x2﹣2x+1中,可得7=x2﹣2x+1,
∴x1=﹣2(舍),x2=6
∴B(6,7),
∵A的坐标为(0,1),
∴直线AB解析式为y=x+1,
∵C(2,﹣1),B(6,7),
∴直线BC解析式为y=2x﹣5.
(2)如图1,
设点P(x0,x0+1),
∴D(,x0+1),
∴PE=x0+1,PD=3﹣x0,
∵△PDF∽△BGN,
∴PF:PD的值固定,
∴PE×PF最大时,PE×PD也最大,
PE×PD=(x0+1)(3﹣x0)=﹣x02+x0+3,
∴当x0=时,PE×PD最大,
即:PE×PF最大.此时G(5,)
∵△MNB是等腰直角三角形,
过B作x轴的平行线,
∴BH=B1H,
GH+BH的最小值转化为求GH+HB1的最小值,
∴当GH和HB1在一条直线上时,GH+HB1的值最小,
此时H(5,6),最小值为7﹣=
(3)令直线BC与x轴交于点I,
∴I(,0)
∴IN=,IN:BN=1:2,
∴沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A′(m,1+2m),C′(2+m,﹣1+2m),2·1·c·n·j·y
∴A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,
当∠A′KC′=90°时,A′K2+KC′2=A′C′2,解得m=,此时t=m=2±;
当∠KC′A′=90°时,KC′2+A′C′2=A′K2,解得m=4,此时t=m=4;
当∠KA′C′=90°时,A′C′2+A′K2=KC′2,解得m=0,此时t=0.
【点评】此题是二次函数综合题,主要考查了相似三角形的性质,待定系数法求函数解析式,两点间的结论公式,解本题的关键是相似三角形的性质的运用.
同课章节目录
