6.1.3 中位数 同步练习
图片预览

文档简介
6.1.3 中位数
核心笔记: 1.中位数:把一组数据按从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
2.中位数的意义:中位数常用来描述“中间位置”或“中等水平”.
基础训练
1.小明记录了一星期每天的最高气温如下表,则这个星期每天最高气温的中位数是( )
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22 ℃ B.23 ℃ C.24 ℃ D.25 ℃
2.已知一组从小到大排列的数据:0,4,x,10的中位数是5,则x=( )
A.5 B.6 C.7 D.8
3.孔明同学参加暑假军事训练的射击成绩如下表:
射击次序
第一次
第二次
第三次
第四次
第五次
成绩(环)
9
8
7
9
6
则孔明射击成绩的中位数是( )
A.6环 B.7环 C.8环 D.9环
4.一组正整数2,3,4,x从小到大排列,已知这组数据的中位数和平均数相等,那么x的值是___________.
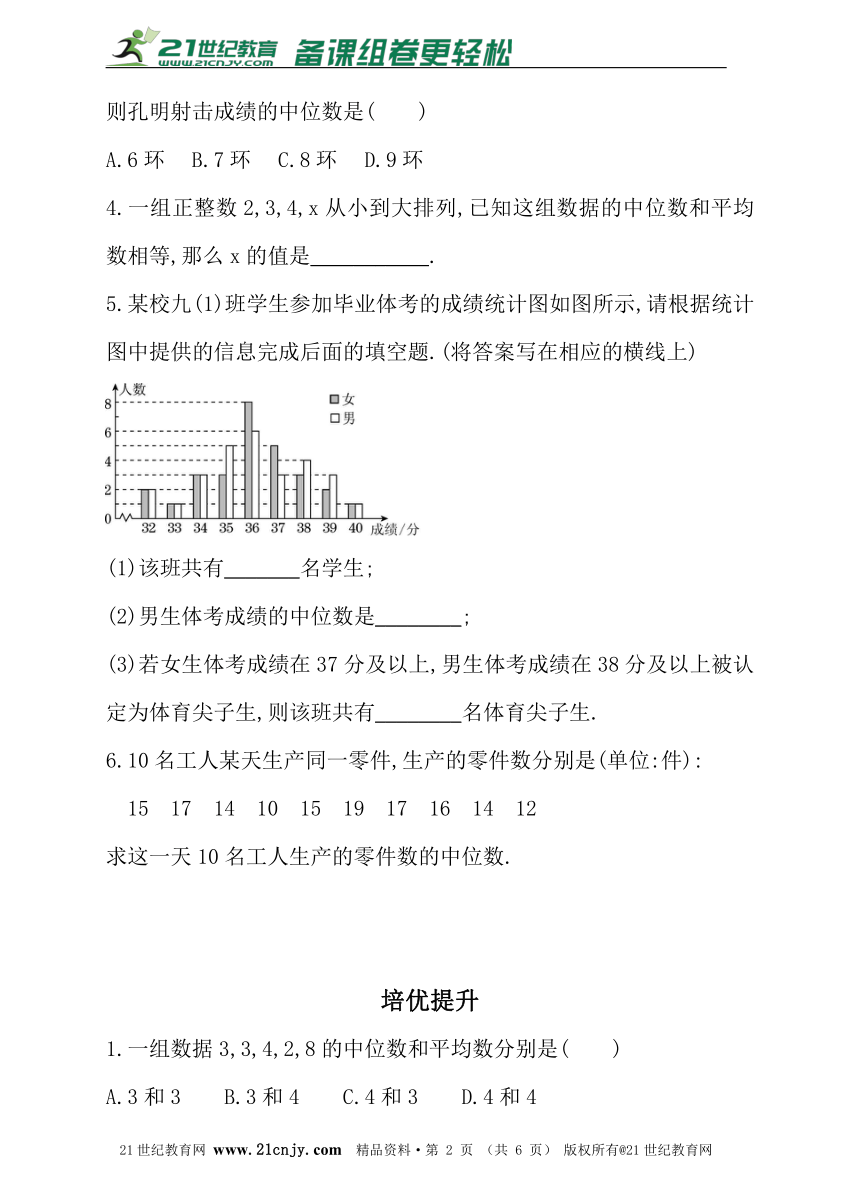
5.某校九(1)班学生参加毕业体考的成绩统计图如图所示,请根据统计图中提供的信息完成后面的填空题.(将答案写在相应的横线上)
(1)该班共有_______名学生;?
(2)男生体考成绩的中位数是________;?
(3)若女生体考成绩在37分及以上,男生体考成绩在38分及以上被认定为体育尖子生,则该班共有________名体育尖子生.?
6.10名工人某天生产同一零件,生产的零件数分别是(单位:件):
15 17 14 10 15 19 17 16 14 12
求这一天10名工人生产的零件数的中位数.
培优提升
1.一组数据3,3,4,2,8的中位数和平均数分别是( )
A.3和3 B.3和4 C.4和3 D.4和4
2.若一组数据1,2,3,4,x的平均数与中位数相同,则x的值不可能是( )
A.0 B.2.5 C.3 D.5
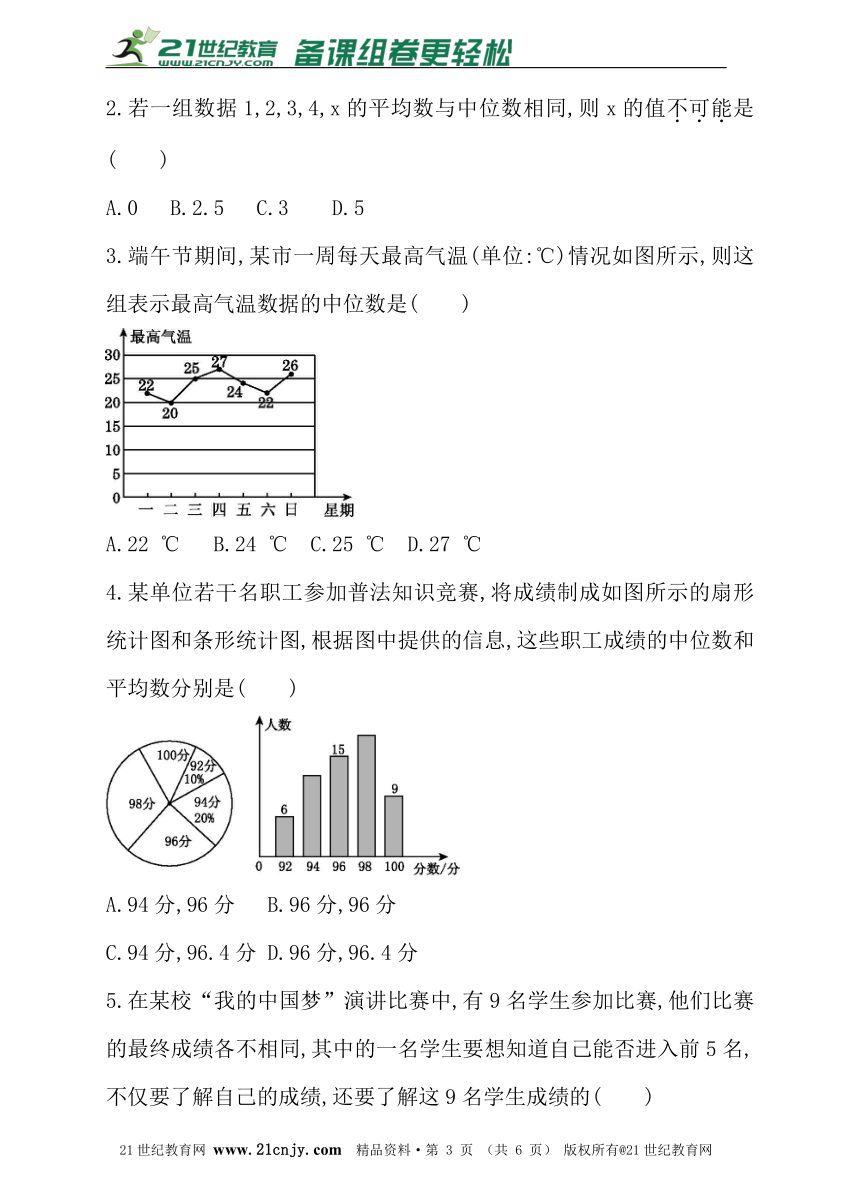
3.端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22 ℃ B.24 ℃ C.25 ℃ D.27 ℃
4.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
5.在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们比赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.加权平均数 B.平均数
C.中位数 D.不能确定
6.某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是________岁.?
7.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为________.?
8. 数据20,16,x的平均数等于中位数,则x=________.?
9.甲班有41名学生,乙班有40名学生.在一次科技知识竞赛中,甲班学生成绩的平均分为86分,中位数为80分;乙班学生成绩的平均分为85分,中位数为85分.
(1)求这两个班81名学生成绩的平均分;(精确到0.1分)
(2)若规定成绩在80分以上(包括80分)为优秀,则两个班81名学生中成绩达到优秀的至少有多少?
(3)甲班成绩的平均分与中位数相差较大,说明什么?
参考答案
【基础训练】
1.【答案】B
2.【答案】B
解:中位数是5,则(4+x)÷2=5,解得x=6.
3.【答案】C
4.【答案】5
解:由中位数和平均数相等,得(3+4)÷2=(2+3+4+x)÷4,解得x=5.
5.【答案】(1)56 (2)36分 (3)19
6.解:将10个数据按从小到大的顺序排
列:10,12,14,14,15,15,16,17,17,19.
位于中间的两个数据都是15,它们的平均数是15,即这组数据的中位数是15.
所以这一天10名工人生产的零件数的中位数是15件.
【培优提升】
1.【答案】B 2.【答案】C 3.【答案】B
4.【答案】D 5.【答案】C 6.【答案】15
7.【答案】1,3,5或2,3,4
解:因为三个数的中位数是3,因此中间的数必是3,而三个数的平均数也是3,则这三个数的和为9,故第一个数与第三个数的和为6,由于是互不相等的正整数,所以这三个数分别为1,3,5或2,3,4.
8.【答案】12或18或24
解:分三种情况讨论,①当x<16时,从小到大排列为x,16,20,故
=16,解得x=12;②当16≤x≤20时,从小到大排列为16,x,20,
故=x,解得x=18;③当x>20时,从小到大排列为16,20,x,故=20,解得x=24.
9.解:(1)这两个班81名学生成绩的平均分
=×(86×41+85×40)≈85.5(分).
(2)甲班学生成绩的中位数为80分,说明至少有21名学生的成绩大于或等于80分;乙班学生成绩的中位数为85分,说明至少有20名学生的成绩大于或等于85分,所以这两个班81名学生中成绩达到优秀的至少有41名.
(3)甲班成绩的平均分与中位数相差较大,说明甲班学生的成绩两极分化比较严重.
解:(3)题答案不唯一.
核心笔记: 1.中位数:把一组数据按从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
2.中位数的意义:中位数常用来描述“中间位置”或“中等水平”.
基础训练
1.小明记录了一星期每天的最高气温如下表,则这个星期每天最高气温的中位数是( )
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22 ℃ B.23 ℃ C.24 ℃ D.25 ℃
2.已知一组从小到大排列的数据:0,4,x,10的中位数是5,则x=( )
A.5 B.6 C.7 D.8
3.孔明同学参加暑假军事训练的射击成绩如下表:
射击次序
第一次
第二次
第三次
第四次
第五次
成绩(环)
9
8
7
9
6
则孔明射击成绩的中位数是( )
A.6环 B.7环 C.8环 D.9环
4.一组正整数2,3,4,x从小到大排列,已知这组数据的中位数和平均数相等,那么x的值是___________.
5.某校九(1)班学生参加毕业体考的成绩统计图如图所示,请根据统计图中提供的信息完成后面的填空题.(将答案写在相应的横线上)
(1)该班共有_______名学生;?
(2)男生体考成绩的中位数是________;?
(3)若女生体考成绩在37分及以上,男生体考成绩在38分及以上被认定为体育尖子生,则该班共有________名体育尖子生.?
6.10名工人某天生产同一零件,生产的零件数分别是(单位:件):
15 17 14 10 15 19 17 16 14 12
求这一天10名工人生产的零件数的中位数.
培优提升
1.一组数据3,3,4,2,8的中位数和平均数分别是( )
A.3和3 B.3和4 C.4和3 D.4和4
2.若一组数据1,2,3,4,x的平均数与中位数相同,则x的值不可能是( )
A.0 B.2.5 C.3 D.5
3.端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22 ℃ B.24 ℃ C.25 ℃ D.27 ℃
4.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
5.在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们比赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.加权平均数 B.平均数
C.中位数 D.不能确定
6.某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是________岁.?
7.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为________.?
8. 数据20,16,x的平均数等于中位数,则x=________.?
9.甲班有41名学生,乙班有40名学生.在一次科技知识竞赛中,甲班学生成绩的平均分为86分,中位数为80分;乙班学生成绩的平均分为85分,中位数为85分.
(1)求这两个班81名学生成绩的平均分;(精确到0.1分)
(2)若规定成绩在80分以上(包括80分)为优秀,则两个班81名学生中成绩达到优秀的至少有多少?
(3)甲班成绩的平均分与中位数相差较大,说明什么?
参考答案
【基础训练】
1.【答案】B
2.【答案】B
解:中位数是5,则(4+x)÷2=5,解得x=6.
3.【答案】C
4.【答案】5
解:由中位数和平均数相等,得(3+4)÷2=(2+3+4+x)÷4,解得x=5.
5.【答案】(1)56 (2)36分 (3)19
6.解:将10个数据按从小到大的顺序排
列:10,12,14,14,15,15,16,17,17,19.
位于中间的两个数据都是15,它们的平均数是15,即这组数据的中位数是15.
所以这一天10名工人生产的零件数的中位数是15件.
【培优提升】
1.【答案】B 2.【答案】C 3.【答案】B
4.【答案】D 5.【答案】C 6.【答案】15
7.【答案】1,3,5或2,3,4
解:因为三个数的中位数是3,因此中间的数必是3,而三个数的平均数也是3,则这三个数的和为9,故第一个数与第三个数的和为6,由于是互不相等的正整数,所以这三个数分别为1,3,5或2,3,4.
8.【答案】12或18或24
解:分三种情况讨论,①当x<16时,从小到大排列为x,16,20,故
=16,解得x=12;②当16≤x≤20时,从小到大排列为16,x,20,
故=x,解得x=18;③当x>20时,从小到大排列为16,20,x,故=20,解得x=24.
9.解:(1)这两个班81名学生成绩的平均分
=×(86×41+85×40)≈85.5(分).
(2)甲班学生成绩的中位数为80分,说明至少有21名学生的成绩大于或等于80分;乙班学生成绩的中位数为85分,说明至少有20名学生的成绩大于或等于85分,所以这两个班81名学生中成绩达到优秀的至少有41名.
(3)甲班成绩的平均分与中位数相差较大,说明甲班学生的成绩两极分化比较严重.
解:(3)题答案不唯一.
