6.2 方差 同步练习
图片预览



文档简介
6.2方差
核心笔记: 1.方差:设一组数据为x1,x2,…,xn,各数据与平均数之差的平方的平均值,叫做这组数据的方差,记做s2,即2·1·c·n·j·y
s2=[++…+].
2.方差的特征:方差反映的是一组数据与其 ( http: / / www.21cnjy.com )平均数的偏离程度.一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.www-2-1-cnjy-com
基础训练
1.下列各统计量中,表示一组数据波动程度的量是( )
A.平均数 B.众数 C.方差 D.频率
2.已知一组数据:1,3,5,5,6,则这组数据的方差是( )
A.16 B.5 C.4 D.3.2
3.教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛.两人在相同条件下各打了5发子弹,命中环数如下:
甲:9,8,7,7,9;
乙:10,8,9,7,6.
应该选( )参加.
A.甲 B.乙
C.甲、乙都可以 D.无法确定
4.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:=2,=1.5,则射击成绩较稳定的是 (填“甲”或“乙”). 21·cn·jy·com
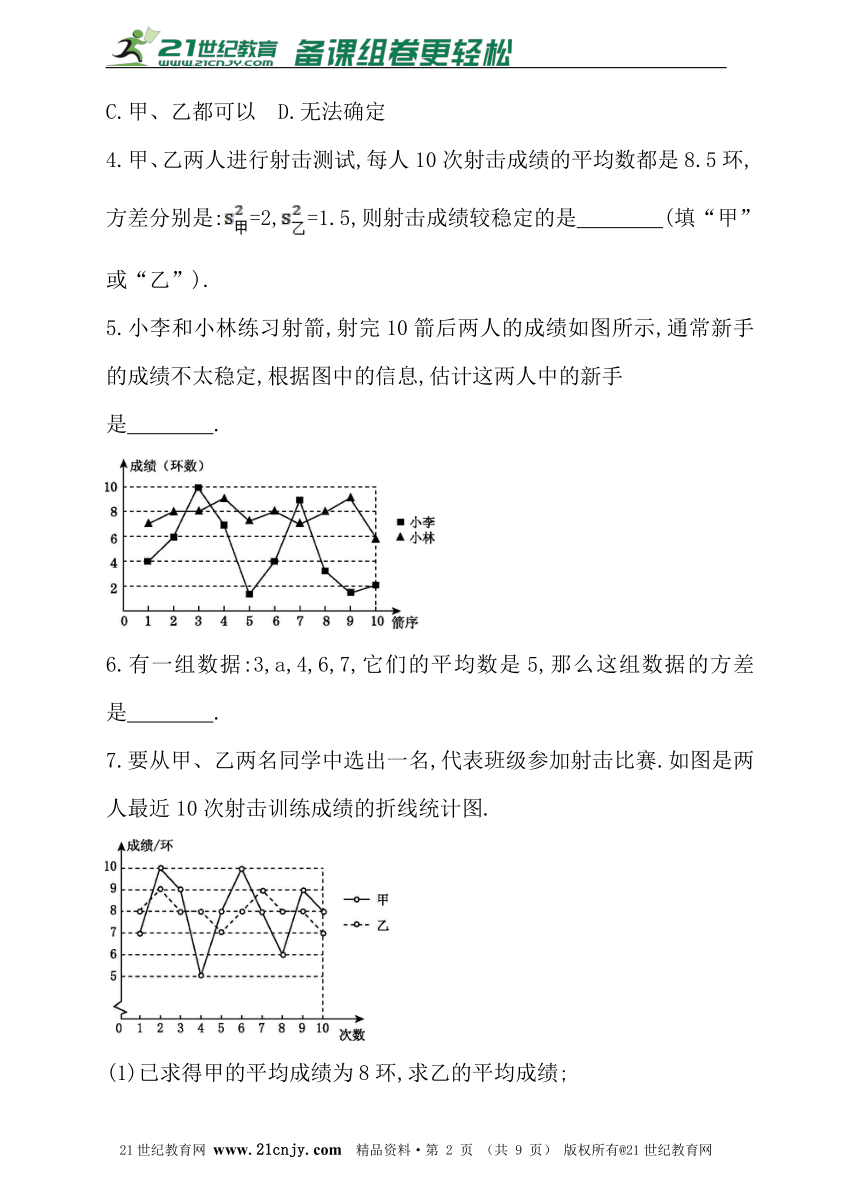
5.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计这两人中的新手
是 .
( http: / / www.21cnjy.com )
6.有一组数据:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是 .
7.要从甲、乙两名同学中选出一名,代表班级参加射击比赛.如图是两人最近10次射击训练成绩的折线统计图.www.21-cn-jy.com
( http: / / www.21cnjy.com )
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察折线统计图,直接写出甲、乙这10次射击成绩的方差,哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选________参赛;
如果其他班级参赛选手的射击成绩都在9环左右,本班应该选________参赛.
培优提升
1.设x1,x2,x3,…,x10的平均数为,方差为s2,若s2=0,则( )
A.=0
B.x1=x2=x3=…=x10
C.x1,x2,…,x10不全为0
D.x1=x2=x3=…=x10=0
2.一组数据a,b,c,d的方差为2,则数据3a,3b,3c,3d的方差为( )
A.2 B.6 C.32 D.18
3.如果给一组数据中每个数减去同一个非零常数,那么该组数据的( )
A.平均数改变,方差不变
B.平均数改变,方差改变
C.平均数不变,方差改变
D.平均数不变,方差不变
4.在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是=0.35,=0.15,=0.25,=0.27,这4人中成绩发挥最稳定的是( )【来源:21·世纪·教育·网】
A.甲 B.乙 C.丙 D.丁
5.若40个数据的平方和是46,平均数是,则这组数据的方差
是 .
6.甲、乙两种水稻实验品种连续5年的平均单位面积产量(单位:t/hm2)如下:
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
经计算,=10,=10,试根据这组数据估计种水稻品种的产量比较稳定.
7.统计学规定:某次测量得到n个结果x1,x2,…,xn.当函数
y=[(x-x1)2+(x-x2)2+…+(x-xn)2]取最小值时,对应x的值称为这次测
量的“最佳近似值”.若某次测量得到5个结果
9.8,10.1,10.5,10.3,9.8.则这次测量的“最佳近似值”
x= ,相应的y= .
8.某厂生产A,B两种产品,其单价随市场变 ( http: / / www.21cnjy.com )化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图如图,并求得了A产品三次单价的平均数和方差:21·世纪*教育网
=5.9;=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
A,B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
( http: / / www.21cnjy.com )
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为 ( http: / / www.21cnjy.com )6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数比B产品这四次单价的中位数的2倍少1,求m的值.21cnjy.com
参考答案
【基础训练】
1.【答案】C
2.【答案】D
解:这组数据的平均数
=(1+3+5+5+6)÷5=4,s2=×[(1-4)2+(3-4)2+(5-4)2+(5-4)2+(6-4)2]=3
.2,故选D.
3.【答案】A
解:由题意可得,
甲的平均数为=8,方差为:
=0.8,同样算得乙的平均数为8,方差为2.
∵0.8<2,∴选择甲射击运动员,故选A.
4.【答案】乙
5.【答案】小李
解:根据图中的信息可知,小李的成绩波动性大,则这两人中的新手是小李.
6.【答案】2
7.解:(1)==8(环).
(2)>.
(3)乙;甲
【培优提升】
1.【答案】B 2.【答案】D 3.【答案】A
4.【答案】B
5.【答案】0.9
解:设这40个数据分别为x1,x2,…,x40.因为
++…+=46,x1+x2+…+x40=×40=20,所以
s2=×[+(-+…+]=×[(-2x1+)+(-2+)+…+(-2x4021教育网
+)]=×[(++…+)-2(x1
++…+)+40]
=×
=×[46-20+10]
=0.9.
6.【答案】甲
7.【答案】10.1;0.076
解:根据题意,x是所有数的平均数,故
x=(9.8+10.1+10.5+10.3+9.8)÷5=10.1,
y=[(9.8-10.1)2+(10.1-10.1)2+(10.5-10.1)2+(10.3-10.1)2+(9.8-10.1)2]=0.076.21世纪教育网版权所有
8.解:(1)如图所示;25
( http: / / www.21cnjy.com )
(2)=×(3.5+4+3)=3.5,
==.
因为<,
所以B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=;
对于B产品,因为m>0,
所以第四次单价大于3元/件.
又因为×2-1=>,
所以第四次单价小于4元/件.
所以×2-1=,
所以m=25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
核心笔记: 1.方差:设一组数据为x1,x2,…,xn,各数据与平均数之差的平方的平均值,叫做这组数据的方差,记做s2,即2·1·c·n·j·y
s2=[++…+].
2.方差的特征:方差反映的是一组数据与其 ( http: / / www.21cnjy.com )平均数的偏离程度.一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.www-2-1-cnjy-com
基础训练
1.下列各统计量中,表示一组数据波动程度的量是( )
A.平均数 B.众数 C.方差 D.频率
2.已知一组数据:1,3,5,5,6,则这组数据的方差是( )
A.16 B.5 C.4 D.3.2
3.教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛.两人在相同条件下各打了5发子弹,命中环数如下:
甲:9,8,7,7,9;
乙:10,8,9,7,6.
应该选( )参加.
A.甲 B.乙
C.甲、乙都可以 D.无法确定
4.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:=2,=1.5,则射击成绩较稳定的是 (填“甲”或“乙”). 21·cn·jy·com
5.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计这两人中的新手
是 .
( http: / / www.21cnjy.com )
6.有一组数据:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是 .
7.要从甲、乙两名同学中选出一名,代表班级参加射击比赛.如图是两人最近10次射击训练成绩的折线统计图.www.21-cn-jy.com
( http: / / www.21cnjy.com )
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察折线统计图,直接写出甲、乙这10次射击成绩的方差,哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选________参赛;
如果其他班级参赛选手的射击成绩都在9环左右,本班应该选________参赛.
培优提升
1.设x1,x2,x3,…,x10的平均数为,方差为s2,若s2=0,则( )
A.=0
B.x1=x2=x3=…=x10
C.x1,x2,…,x10不全为0
D.x1=x2=x3=…=x10=0
2.一组数据a,b,c,d的方差为2,则数据3a,3b,3c,3d的方差为( )
A.2 B.6 C.32 D.18
3.如果给一组数据中每个数减去同一个非零常数,那么该组数据的( )
A.平均数改变,方差不变
B.平均数改变,方差改变
C.平均数不变,方差改变
D.平均数不变,方差不变
4.在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是=0.35,=0.15,=0.25,=0.27,这4人中成绩发挥最稳定的是( )【来源:21·世纪·教育·网】
A.甲 B.乙 C.丙 D.丁
5.若40个数据的平方和是46,平均数是,则这组数据的方差
是 .
6.甲、乙两种水稻实验品种连续5年的平均单位面积产量(单位:t/hm2)如下:
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
经计算,=10,=10,试根据这组数据估计种水稻品种的产量比较稳定.
7.统计学规定:某次测量得到n个结果x1,x2,…,xn.当函数
y=[(x-x1)2+(x-x2)2+…+(x-xn)2]取最小值时,对应x的值称为这次测
量的“最佳近似值”.若某次测量得到5个结果
9.8,10.1,10.5,10.3,9.8.则这次测量的“最佳近似值”
x= ,相应的y= .
8.某厂生产A,B两种产品,其单价随市场变 ( http: / / www.21cnjy.com )化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图如图,并求得了A产品三次单价的平均数和方差:21·世纪*教育网
=5.9;=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
A,B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
( http: / / www.21cnjy.com )
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为 ( http: / / www.21cnjy.com )6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数比B产品这四次单价的中位数的2倍少1,求m的值.21cnjy.com
参考答案
【基础训练】
1.【答案】C
2.【答案】D
解:这组数据的平均数
=(1+3+5+5+6)÷5=4,s2=×[(1-4)2+(3-4)2+(5-4)2+(5-4)2+(6-4)2]=3
.2,故选D.
3.【答案】A
解:由题意可得,
甲的平均数为=8,方差为:
=0.8,同样算得乙的平均数为8,方差为2.
∵0.8<2,∴选择甲射击运动员,故选A.
4.【答案】乙
5.【答案】小李
解:根据图中的信息可知,小李的成绩波动性大,则这两人中的新手是小李.
6.【答案】2
7.解:(1)==8(环).
(2)>.
(3)乙;甲
【培优提升】
1.【答案】B 2.【答案】D 3.【答案】A
4.【答案】B
5.【答案】0.9
解:设这40个数据分别为x1,x2,…,x40.因为
++…+=46,x1+x2+…+x40=×40=20,所以
s2=×[+(-+…+]=×[(-2x1+)+(-2+)+…+(-2x4021教育网
+)]=×[(++…+)-2(x1
++…+)+40]
=×
=×[46-20+10]
=0.9.
6.【答案】甲
7.【答案】10.1;0.076
解:根据题意,x是所有数的平均数,故
x=(9.8+10.1+10.5+10.3+9.8)÷5=10.1,
y=[(9.8-10.1)2+(10.1-10.1)2+(10.5-10.1)2+(10.3-10.1)2+(9.8-10.1)2]=0.076.21世纪教育网版权所有
8.解:(1)如图所示;25
( http: / / www.21cnjy.com )
(2)=×(3.5+4+3)=3.5,
==.
因为<,
所以B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=;
对于B产品,因为m>0,
所以第四次单价大于3元/件.
又因为×2-1=>,
所以第四次单价小于4元/件.
所以×2-1=,
所以m=25.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
