9.2.1 一元一次不等式及其解法 同步练习
文档属性
| 名称 | 9.2.1 一元一次不等式及其解法 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-25 21:07:32 | ||
图片预览


文档简介
9.2.1 一元一次不等式及其解法
基础训练
知识点1 一元一次不等式
1.下列不等式中,是一元一次不等式的是( )
A.x-<0 B.a2+b2>0
C.>1 D.x2.若(m+1)x|m|+2>0是关于x的一元一次不等式,则m=( )
A.±1 B.1 C.-1 D.0
知识点2 一元一次不等式的解法
3.解不等式-≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
4.解不等式>的过程中,出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项,得5x-6x>-10-3;
④系数化为1,得x>13.
A.① B.② C.③ D.④
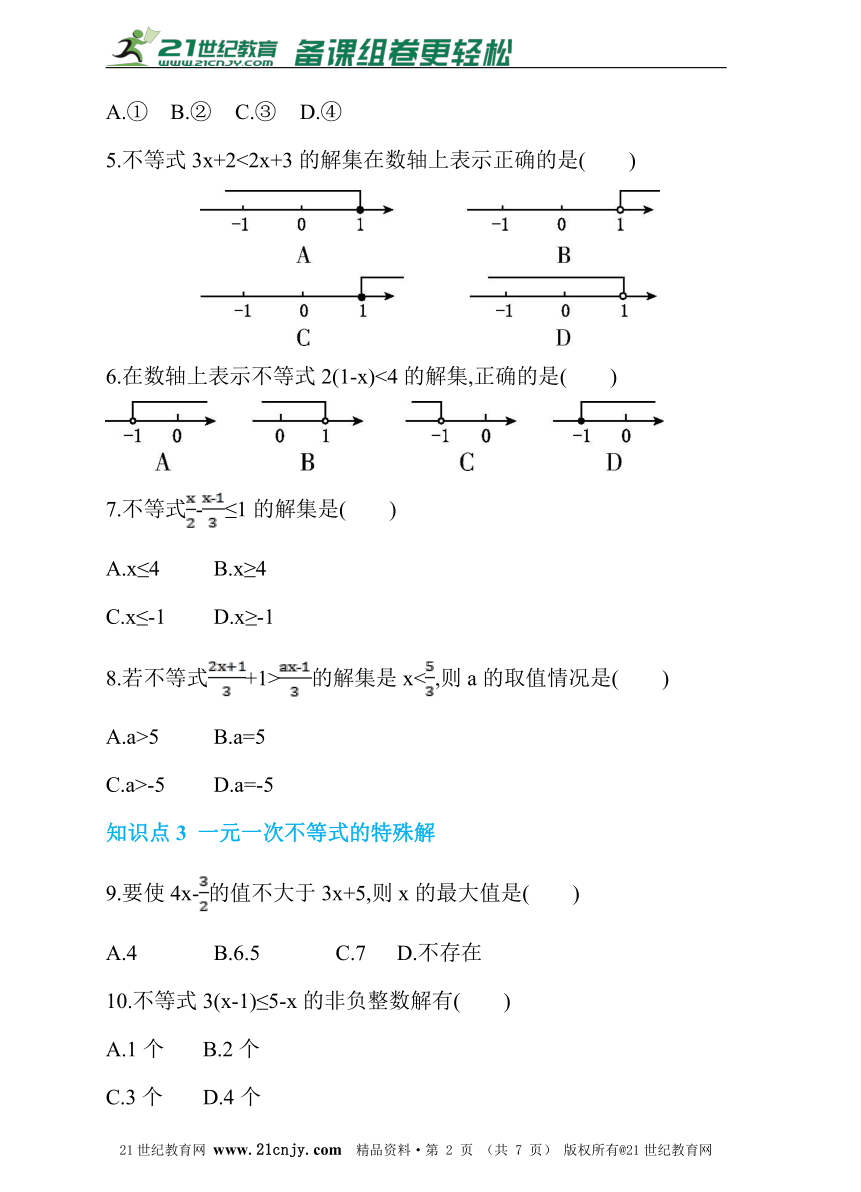
5.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
6.在数轴上表示不等式2(1-x)<4的解集,正确的是( )
7.不等式-≤1的解集是( )
A.x≤4 B.x≥4
C.x≤-1 D.x≥-1
8.若不等式+1>的解集是x<,则a的取值情况是( )
A.a>5 B.a=5
C.a>-5 D.a=-5
知识点3 一元一次不等式的特殊解
9.要使4x-的值不大于3x+5,则x的最大值是( )
A.4 B.6.5 C.7 D.不存在
10.不等式3(x-1)≤5-x的非负整数解有( )
A.1个 B.2个
C.3个 D.4个
11.关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A.-3C.-3≤b≤-2 D.-3≤b<-2
12.当自然数k=________时,关于x的方程x-3k=5(x-k)+6的解是负数.
13.下列不等式中,是一元一次不等式的是( )
A.2x2-5>0 B.+x<5
C.-5y+8>0 D.2x+3>2(1+x)
提升训练
考查角度1 利用不等式的性质解简单的不等式
14.解不等式:≤-1,并把解集表示在数轴上.
考查角度2 利用不等式的性质解较复杂的不等式
15.解不等式->.
考查角度3 利用解不等式求特殊解
16.求不等式->+的正整数解.
考查角度4 利用不等式的解集求字母的值
17.不等式(x-m)>3-m的解集为x>1,求m的值.
探究培优
拔尖角度1利用解不等式解与方程组的解有关的综合问题
18.若关于x,y的二元一次方程组的解满足x+y>-,求出满足条件的m的所有正整数值.
拔尖角度2 利用不等式的解集求字母的取值范围
19.关于x的两个不等式①<1与②1-3x>0
(1)若两个不等式的解集相同,求a的值;
(2)若不等式①的解都是②的解,求a的取值范围.
参考答案
1.【答案】A
2.【答案】B
解:∵(m+1)x|m|+2>0是关于x的一元一次不等式,∴m+1≠0.|m|=1,解得m=1,故选B.
3.【答案】D 4.【答案】D 5.【答案】D 6.【答案】A
7.【答案】A
解:去分母,得3x-2(x-1)≤6,去括号,得3x-2x+2≤6,移项,合并同类项,得x≤4.故选A.
8.【答案】B
解:不等式+1>可以转化为(2-a)x>-5.由题意知x<,所以知2-a<0,即a>2.所以x<,即=.所以2-a=-3.所以a=5.故选B.
9.【答案】B 10.【答案】C
11.【答案】D
解:由不等式x-b>0,解得x>b,∵不等式只有两个负整数解,∴-3≤b<-2,故选D.
12.【答案】0,1,2
13.【答案】C
解:此题学生常常不化简直接进行判断而错选D.
14.解:去分母得,4(2x-1)≤3(3x+2)-12,去括号得,8x-4≤9x+6-12,移项得,8x-9x≤6-12+4,合并同类项得,-x≤-2,把x的系数化为1得,x≥2.
解集在数轴上表示如图:
15.解:->.
整理,得4x-3-15x+3>19-30x.
移项、合并同类项,得19x>19.
系数化为1,得x>1.
分析:不等式的化简是为了计算的方便,当不等式的形式较复杂时,一定要先进行化简.
16.解:去分母,得3(2-3x)-3(x-5)>2(-4x+1)+8.
去括号,得6-9x-3x+15>-8x+2+8.
移项、合并同类项,得-4x>-11.
系数化为1,得x<.
因为小于的正整数有1,2,所以这个不等式的正整数解是1,2.
分析:求不等式的特殊解时,应先求出不等式的解集,然后在解集中确定符合要求的特殊解.
17.解:去分母,得x-m>3(3-m),
去括号、移项、合并同类项,得x>9-2m.
又因为不等式的解集为x>1,所以9-2m=1,解得m=4.
18.解:
①+②得:3(x+y)=-3m+6,∴x+y=-m+2.∵x+y>-,
∴-m+2>-.解得m<.
∵m为正整数,∴m=1,2,3.
19.解:(1)由①得x<,
由②得x<,
由两个不等式的解集相同得=,
解得a=1.
(2)由不等式①的解都是②的解得≤,
解得a≥1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
基础训练
知识点1 一元一次不等式
1.下列不等式中,是一元一次不等式的是( )
A.x-<0 B.a2+b2>0
C.>1 D.x
A.±1 B.1 C.-1 D.0
知识点2 一元一次不等式的解法
3.解不等式-≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
4.解不等式>的过程中,出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项,得5x-6x>-10-3;
④系数化为1,得x>13.
A.① B.② C.③ D.④
5.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
6.在数轴上表示不等式2(1-x)<4的解集,正确的是( )
7.不等式-≤1的解集是( )
A.x≤4 B.x≥4
C.x≤-1 D.x≥-1
8.若不等式+1>的解集是x<,则a的取值情况是( )
A.a>5 B.a=5
C.a>-5 D.a=-5
知识点3 一元一次不等式的特殊解
9.要使4x-的值不大于3x+5,则x的最大值是( )
A.4 B.6.5 C.7 D.不存在
10.不等式3(x-1)≤5-x的非负整数解有( )
A.1个 B.2个
C.3个 D.4个
11.关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A.-3
12.当自然数k=________时,关于x的方程x-3k=5(x-k)+6的解是负数.
13.下列不等式中,是一元一次不等式的是( )
A.2x2-5>0 B.+x<5
C.-5y+8>0 D.2x+3>2(1+x)
提升训练
考查角度1 利用不等式的性质解简单的不等式
14.解不等式:≤-1,并把解集表示在数轴上.
考查角度2 利用不等式的性质解较复杂的不等式
15.解不等式->.
考查角度3 利用解不等式求特殊解
16.求不等式->+的正整数解.
考查角度4 利用不等式的解集求字母的值
17.不等式(x-m)>3-m的解集为x>1,求m的值.
探究培优
拔尖角度1利用解不等式解与方程组的解有关的综合问题
18.若关于x,y的二元一次方程组的解满足x+y>-,求出满足条件的m的所有正整数值.
拔尖角度2 利用不等式的解集求字母的取值范围
19.关于x的两个不等式①<1与②1-3x>0
(1)若两个不等式的解集相同,求a的值;
(2)若不等式①的解都是②的解,求a的取值范围.
参考答案
1.【答案】A
2.【答案】B
解:∵(m+1)x|m|+2>0是关于x的一元一次不等式,∴m+1≠0.|m|=1,解得m=1,故选B.
3.【答案】D 4.【答案】D 5.【答案】D 6.【答案】A
7.【答案】A
解:去分母,得3x-2(x-1)≤6,去括号,得3x-2x+2≤6,移项,合并同类项,得x≤4.故选A.
8.【答案】B
解:不等式+1>可以转化为(2-a)x>-5.由题意知x<,所以知2-a<0,即a>2.所以x<,即=.所以2-a=-3.所以a=5.故选B.
9.【答案】B 10.【答案】C
11.【答案】D
解:由不等式x-b>0,解得x>b,∵不等式只有两个负整数解,∴-3≤b<-2,故选D.
12.【答案】0,1,2
13.【答案】C
解:此题学生常常不化简直接进行判断而错选D.
14.解:去分母得,4(2x-1)≤3(3x+2)-12,去括号得,8x-4≤9x+6-12,移项得,8x-9x≤6-12+4,合并同类项得,-x≤-2,把x的系数化为1得,x≥2.
解集在数轴上表示如图:
15.解:->.
整理,得4x-3-15x+3>19-30x.
移项、合并同类项,得19x>19.
系数化为1,得x>1.
分析:不等式的化简是为了计算的方便,当不等式的形式较复杂时,一定要先进行化简.
16.解:去分母,得3(2-3x)-3(x-5)>2(-4x+1)+8.
去括号,得6-9x-3x+15>-8x+2+8.
移项、合并同类项,得-4x>-11.
系数化为1,得x<.
因为小于的正整数有1,2,所以这个不等式的正整数解是1,2.
分析:求不等式的特殊解时,应先求出不等式的解集,然后在解集中确定符合要求的特殊解.
17.解:去分母,得x-m>3(3-m),
去括号、移项、合并同类项,得x>9-2m.
又因为不等式的解集为x>1,所以9-2m=1,解得m=4.
18.解:
①+②得:3(x+y)=-3m+6,∴x+y=-m+2.∵x+y>-,
∴-m+2>-.解得m<.
∵m为正整数,∴m=1,2,3.
19.解:(1)由①得x<,
由②得x<,
由两个不等式的解集相同得=,
解得a=1.
(2)由不等式①的解都是②的解得≤,
解得a≥1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
