福建省泉州市鹏峰中学2016-2017学年八年级(上)期中数学试卷(解析版)
文档属性
| 名称 | 福建省泉州市鹏峰中学2016-2017学年八年级(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-26 09:36:08 | ||
图片预览




文档简介
2016-2017学年福建省泉州市鹏峰中学八年级(上)期中数学试卷
一.选择题:(每小题4分,共40分)
1.4的平方根是( )
A.﹣2
B.2
C.±2
D.4
2.下列运算正确的是( )
A.(﹣3x)2=9x2
B.x x2=x2
C.(a3)2=9
D.a6÷a2=a3
3.下列命题是真命题的是( )
A.是无理数
B.﹣27没有立方根
C.相等的角是对顶角
D.全等三角形的对应边相等
4.下列各式由左边到右边的变形中,是因式分解的是( )
A.a2﹣3a+2=a(a﹣3)
B.a2x﹣a=a(ax﹣1)
C.x2+3x+9=(x+3)2
D.(x+1)(x﹣1)=x2﹣1
5.下列选项中,可用来说明命题“任何偶数都是8的倍数”是假命题的反例是( )
A.15
B.24
C.42
D.2k
6.如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( )
A.80°
B.60°
C.40°
D.20°
7.若x2+mx﹣15=(x+3)(x+n),则m的值是( )
A.﹣5
B.5
C.﹣2
D.2
8.若3x﹣2nym与xmy﹣3n的积与x4y3是同类项,则m+2n的立方根( )
A.﹣2
B.2
C.±2
D.8
9.若a﹣b=1,ab=4,则下列代数式a3b﹣2a2b2+ab3的值( )
A.3
B.4
C.5
D.6
10.如果一长方形的面积为2x2+x,它的一条边长为x,则它的周长为( )
A.2x+1
B.3x+1
C.6x+1
D.6x+2
二、填空题:(每小题4分,共40分)
11.设整数m满足﹣<m<,则m的个数是 .
12.命题“等角的余角相等”的条件是“两个角相等”,则结论是 .
13.如图,AC=AD,请你添加一个条件,根据“边角边”判定△ADB≌△ACB,你所添加的条件是 .
14.如果am=3,a2m+n=36,则an的值是 .
15.若a﹣b=1,则代数式a2﹣b2﹣2b的值为 .
16.已知a,b是△ABC的两边长,且满足a2﹣10a+=﹣25,则第三边c的取值范围是 .
三、解答题:
17.计算:
(1)(﹣1)2016+×+
(2)4x2 x+6x5y3÷(﹣3x2y3)
(3)(x+1)(x2﹣x+1)
(4)(2+a)(2﹣a)+(a+3)2.
18.因式分解:
(1)4x3﹣8x2+4x
(2)x2(a﹣1)+1﹣a.
19.化简求值:(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1),其中x,y的值满足y=+﹣1.
20.一个长方形活动场地的长为2am,宽比长少5m,实施“阳光体育”行动后,学校将长方形的长与宽都增加了4m,则
(1)扩大后长方形的宽为 m(用含a的代数式表示);
(2)求场地面积增加了多少m2?
21.如图,已知点E,C在线段BF上,AB=DE,AC=DF,∠A=∠D,
求证:(1)△ABC≌△DEF
(2)AB∥DE.
22.拼图与数学:
(1)如图1,观察左边方格图中阴影所示的图形(注:每一小方格的边长为1).若将它剪开,可重新拼成一个正方形,请你在右边的方格图中画出你所拼成的正方形,可用阴影增加效果,并写出你所拼成的正方形的边长 ;
(2)如图2是用4个相同的小长方形与1个正方形镶嵌而成的正方形图案.若用x、y表示小长方形的两边长(x>y),则请利用图中的面积关系直接写来代数式x+y、x﹣y、xy三者之间存在着等式关系: ;
(3)如图3,右图是2002年在北京召开的国际数学家大会的会标,它来源于我国古代著名的“赵爽弦图”.它是由4个全等的直角三角形(如左图,三边长分别为BC=a、AC=b、AB=c)及中间一个小正方形拼成的大正方形.请你利用图中的面积关系推导出一个有关直角三角形三边长a、b、c简洁的等量关系.
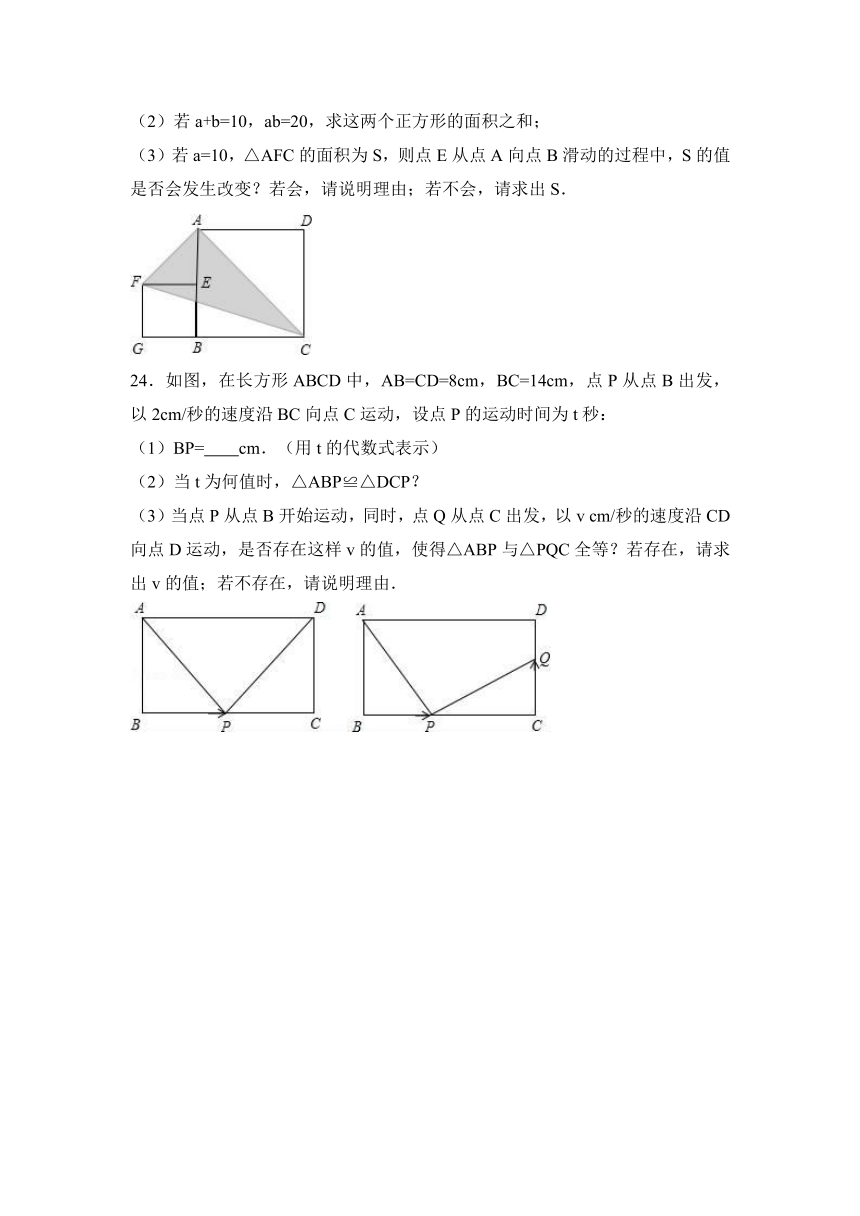
23.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
(1)用含a、b的代数式表示AE= ;
(2)若a+b=10,ab=20,求这两个正方形的面积之和;
(3)若a=10,△AFC的面积为S,则点E从点A向点B滑动的过程中,S的值是否会发生改变?若会,请说明理由;若不会,请求出S.
24.如图,在长方形ABCD中,AB=CD=8cm,BC=14cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)BP= cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
2016-2017学年福建省泉州市鹏峰中学八年级(上)期中数学试卷
参考答案与试题解析
一.选择题:(每小题4分,共40分)
1.4的平方根是( )
A.﹣2
B.2
C.±2
D.4
【考点】平方根.
【分析】首先根据平方根的定义求出4的平方根,然后就可以解决问题.
【解答】解:∵±2的平方等于4,
∴4的平方根是:±2.
故选C.
2.下列运算正确的是( )
A.(﹣3x)2=9x2
B.x x2=x2
C.(a3)2=9
D.a6÷a2=a3
【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.
【分析】结合同底数幂的除法、同底数幂的乘法、幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:A、(﹣3x)2=9x2,本选项正确;
B、x x2=x3≠x2,本选项错误;
C、(a3)2=a6≠a9,本选项错误;
D、a6÷a2=a4≠a3,本选项错误.
故选A.
3.下列命题是真命题的是( )
A.是无理数
B.﹣27没有立方根
C.相等的角是对顶角
D.全等三角形的对应边相等
【考点】命题与定理.
【分析】根据算术平方根的概念、立方根的概念、对顶角的定义、全等三角形的性质进行判断即可.
【解答】解:
=3是有理数,A错误;
﹣27的立方根是﹣3,B错误;
相等的角不一定是对顶角,C错误;
全等三角形的对应边相等,D正确,
故选:D.
4.下列各式由左边到右边的变形中,是因式分解的是( )
A.a2﹣3a+2=a(a﹣3)
B.a2x﹣a=a(ax﹣1)
C.x2+3x+9=(x+3)2
D.(x+1)(x﹣1)=x2﹣1
【考点】因式分解的意义.
【分析】利用因式分解的定义判断即可.
【解答】解:下列各式由左边到右边的变形中,是因式分解的是a2x﹣a=a(ax﹣1),
故选B
5.下列选项中,可用来说明命题“任何偶数都是8的倍数”是假命题的反例是( )
A.15
B.24
C.42
D.2k
【考点】命题与定理.
【分析】根据偶数与倍数的定义对各选项进行验证即可.
【解答】解:A、15不是偶数,故本选项错误;
B、24是8的倍数,故本选项错误;
C、42是偶数但不是8的倍数,故本选项正确;
D、2k是偶数,但不一定是8的倍数,故本选项错误;
故选C.
6.如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( )
A.80°
B.60°
C.40°
D.20°
【考点】全等三角形的性质.
【分析】根据三角形内角和定理可求∠ABC=60°,根据全等三角形的性质可证∠DCB=∠ABC,即可求∠DCB.
【解答】解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,∠ABC=∠DCB,
△ABC中,∠A=80°,∠ACB=40°,
∴∠ABC=180°﹣80°﹣40°=60°,
∴∠BCD=∠ABC=60°,
故选B.
7.若x2+mx﹣15=(x+3)(x+n),则m的值是( )
A.﹣5
B.5
C.﹣2
D.2
【考点】因式分解的意义.
【分析】把等式的右边展开得:x2+mx﹣15=x2+nx+3x+3n,然后根据对应项系数相等列式求解即可.
【解答】解:∵x2+mx﹣15=(x+3)(x+n),
∴x2+mx﹣15=x2+nx+3x+3n,
∴3n=﹣15,m=n+3,
解得n=﹣5,m=﹣5+3=﹣2.
故选C.
8.若3x﹣2nym与xmy﹣3n的积与x4y3是同类项,则m+2n的立方根( )
A.﹣2
B.2
C.±2
D.8
【考点】单项式乘单项式;立方根;同类项.
【分析】先依据单项式乘单项式法则计算,然后依据同类项的定义得到关于m、n的方程组,于是可求得m、n的值,然后再求得m+2n的值,最后求立方根即可.
【解答】解:3x﹣2nym xmy﹣3n=3xm﹣2nym﹣3n.
∵3x﹣2nym与xmy﹣3n的积与()4y3是同类项,
∴m﹣2n=4,m﹣3n=3,
解得n=1,m=6.
∴m+2n=8.
∴m+2n的立方根为2.
故选:B.
9.若a﹣b=1,ab=4,则下列代数式a3b﹣2a2b2+ab3的值( )
A.3
B.4
C.5
D.6
【考点】因式分解的应用.
【分析】提取公因式ab后再利用完全平方公式因式分解后整体代入即可求解.
【解答】解:a3b﹣2a2b2+ab3=ab(a﹣b)2=4×1=4.
故选:B.
10.如果一长方形的面积为2x2+x,它的一条边长为x,则它的周长为( )
A.2x+1
B.3x+1
C.6x+1
D.6x+2
【考点】整式的除法.
【分析】根据整式的除法,可得另一边长,根据整式的加法,可得答案.
【解答】解:另一边长为(2x2+x)÷x=2x+1,
周长为2[x+(2x+1)]=2(x+2x+1)=6x+2,
故选:D.
二、填空题:(每小题4分,共40分)
11.设整数m满足﹣<m<,则m的个数是 4 .
【考点】估算无理数的大小.
【分析】直接利用,的取值范围,进而得出符合题意的个数.
【解答】解:∵整数m满足﹣<m<,
∴m可以为:﹣1,0,1,2,
∴m的个数为4个.
故答案为:4.
12.命题“等角的余角相等”的条件是“两个角相等”,则结论是 它们的余角相等 .
【考点】命题与定理.
【分析】命题的已知部分是条件,即题设,由条件得出结果是结论.
【解答】解:“等角的余角相等”的条件是“两个角相等”,则结论是它们的余角相等;
故答案为:它们的余角相等.
13.如图,AC=AD,请你添加一个条件,根据“边角边”判定△ADB≌△ACB,你所添加的条件是 ∠CAB=∠DAB .
【考点】全等三角形的判定.
【分析】根据AC=AD,AB为公共边可知需要添加∠CAB=∠DAB.
【解答】解:在△ADB与△ACB中,
∵,
∴△ADB≌△ACB(SAS).
故答案为:∠CAB=∠DAB.
14.如果am=3,a2m+n=36,则an的值是 4 .
【考点】幂的乘方与积的乘方;同底数幂的乘法.
【分析】先将a2m+n变形为(am)2×an,然后结合幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:∵am=3,a2m+n=36=(am)2×an,
∴an
=a2m+n÷(am)2
=36÷32
=36÷9
=4.
故答案为:4.
15.若a﹣b=1,则代数式a2﹣b2﹣2b的值为 1 .
【考点】完全平方公式.
【分析】运用平方差公式,化简代入求值,
【解答】解:因为a﹣b=1,
a2﹣b2﹣2b=(a+b)(a﹣b)﹣2b=a+b﹣2b=a﹣b=1,
故答案为:1.
16.已知a,b是△ABC的两边长,且满足a2﹣10a+=﹣25,则第三边c的取值范围是 2<c<8 .
【考点】三角形三边关系.
【分析】已知等式左边前三项利用完全平方公式变形后,根据非负数的性质求出a与b的值,即可确定出c的范围.
【解答】解:∵a2﹣10a+25+=(a﹣5)2+=0,
∴a﹣5=0,b﹣3=0,即a=5,b=3,
则第三边c的取值范围是2<c<8.
故答案为:2<c<8.
三、解答题:
17.计算:
(1)(﹣1)2016+×+
(2)4x2 x+6x5y3÷(﹣3x2y3)
(3)(x+1)(x2﹣x+1)
(4)(2+a)(2﹣a)+(a+3)2.
【考点】整式的混合运算;实数的运算.
【分析】根据整式的混合运算法则、实数的性质解答即可.
【解答】解:(1)(﹣1)2016+×+=1﹣×5+2=1;
(2)4x2 x+6x5y3÷(﹣3x2y3)=10x3﹣2x3=8x3;
(3)(x+1)(x2﹣x+1)=x3﹣x2+x+x2﹣x+1=x3+1;
(4)(2+a)(2﹣a)+(a+3)2=4﹣a2+a2+6a+9=6a+13.
18.因式分解:
(1)4x3﹣8x2+4x
(2)x2(a﹣1)+1﹣a.
【考点】提公因式法与公式法的综合运用.
【分析】(1)先提公因式,然后利用完全平方公式分解因式;
(2)先提公因式,然后利用平方差公式分解因式.
【解答】解:(1)原式=4x(x2﹣2x+1)
=4x(x﹣1)2;
(2)原式=(a﹣1)(x2﹣1)
=(a﹣1)(x+1)(x﹣1).
19.化简求值:(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1),其中x,y的值满足y=+﹣1.
【考点】整式的混合运算—化简求值;二次根式有意义的条件.
【分析】先求出x、y的值,算乘法和除法,再合并同类项,最后代入求出即可.
【解答】解;∵x,y的值满足y=+﹣1,
∴x﹣3≥0且3﹣x≥0,
∴x=3,
∴y=﹣1,
(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1)
=3x2+2xy+x2﹣2xy+y2﹣4x2+1
=y2+1
=(﹣1)2+1
=2.
20.一个长方形活动场地的长为2am,宽比长少5m,实施“阳光体育”行动后,学校将长方形的长与宽都增加了4m,则
(1)扩大后长方形的宽为 2a﹣1 m(用含a的代数式表示);
(2)求场地面积增加了多少m2?
【考点】整式的混合运算.
【分析】(1)根据题意即可得到结论;
(2)根据矩形
面积公式即可得到结论.
【解答】解:(1)∵长方形活动场地的长为2am,宽比长少5m,
∴宽是2a﹣5,
∵将长方形的长与宽都增加了4m,
∴扩大后长方形的宽为2a﹣1,
故答案为:2a﹣1;
(2)(2a+4)(2a﹣1)﹣2a(2a﹣5)=16a﹣4m2,
∴场地面积增加了多少(16a﹣4)m2.
21.如图,已知点E,C在线段BF上,AB=DE,AC=DF,∠A=∠D,
求证:(1)△ABC≌△DEF
(2)AB∥DE.
【考点】全等三角形的判定与性质.
【分析】(1)根据SAS即可证明.
(2)利用全等三角形的性质可得∠B=∠DEC,由此可以推出AB∥DE.
【解答】证明:(1)在△BAC和△EDC中,
,
∴△BAC≌△EDC(SAS).
(2)∵△BAC≌△EDC,
∴∠B=∠EDC,
∴AB∥DE.
22.拼图与数学:
(1)如图1,观察左边方格图中阴影所示的图形(注:每一小方格的边长为1).若将它剪开,可重新拼成一个正方形,请你在右边的方格图中画出你所拼成的正方形,可用阴影增加效果,并写出你所拼成的正方形的边长 ;
(2)如图2是用4个相同的小长方形与1个正方形镶嵌而成的正方形图案.若用x、y表示小长方形的两边长(x>y),则请利用图中的面积关系直接写来代数式x+y、x﹣y、xy三者之间存在着等式关系: (x+y)2﹣4xy=(x﹣y)2 ;
(3)如图3,右图是2002年在北京召开的国际数学家大会的会标,它来源于我国古代著名的“赵爽弦图”.它是由4个全等的直角三角形(如左图,三边长分别为BC=a、AC=b、AB=c)及中间一个小正方形拼成的大正方形.请你利用图中的面积关系推导出一个有关直角三角形三边长a、b、c简洁的等量关系.
【考点】勾股定理的证明.
【分析】(1)根据正方形的面积求出边长,即可得解;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式x+y、x﹣y、xy之间的等量关系.
(3)先表示出中间小正方形的边长,然后根据大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积列出等式,然后整理即可得解.
【解答】解:(1)如图1所示:
(2)代数式x+y、x﹣y、xy三者之间存在着等式关系:(x+y)2﹣4xy=(x﹣y)2;
(3)它能说明的等式为:c2=a2+b2.
推导如下:中间小正方形的边长为(b﹣a),
∴大正方形的面积可表示为:
c2=4×ab+(b﹣a)2,
整理得,c2=2ab+b2﹣2ab+a2,
即c2=a2+b2.
故答案为:;(x+y)2﹣4xy=(x﹣y)2.
23.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
(1)用含a、b的代数式表示AE= a﹣b ;
(2)若a+b=10,ab=20,求这两个正方形的面积之和;
(3)若a=10,△AFC的面积为S,则点E从点A向点B滑动的过程中,S的值是否会发生改变?若会,请说明理由;若不会,请求出S.
【考点】完全平方公式的几何背景.
【分析】(1)根据题意可知:AE=AB﹣BE=a﹣b;
(2)根据完全平方公式即可求出答案.
(3)设CF与AB交于点H,分别求出AH、EF、BC的长度即可求出S的值.
【解答】解:(1)AE=AB﹣BE=a﹣b
(2)∵(a+b)2=a2+2ab+b2,
∴这两个正方形的面积之和为:a2+b2=(a+b)2﹣2ab=100﹣40=60
(3)设CF与AB交于H,
∴BC=10,GB=GF=b,
∵BH∥GF,
∴△BCH∽△GCF
∴,
∴BH=,
∴AH=AB﹣BH=,
∴S=S△AFH+S△CHA
=AH GB+AH BC
=AH(GB+BC)
=AH GC
=××(10+b)
=50
∴S的值不会发生改变;
24.如图,在长方形ABCD中,AB=CD=8cm,BC=14cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)BP= 2t cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
【考点】四边形综合题.
【分析】(1)根据P点的运动速度可得BP的长;
(2)根据全等三角形的性质即可得出BP=CP即可;
(3)此题主要分两种情况①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
【解答】解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,
则PC=14﹣2t;
(2)当t=时,△ABP≌△DCP,
理由:∵BP=2t,CP=14﹣2t,
∵△ABP≌△DCP,
∴BP=CP,
∴2t=14﹣2t,
∴t=,
(2)①当△ABP≌△PCQ时,
∴BP=CQ,AB=PC,
∵AB=8,
∴PC=8,
∴BP=BC﹣PC=14﹣8=6,
2t=6,
解得:t=3,
CQ=BP=6,
v×3=6,
解得:v=2;
②当△ABP≌△QCP时,
∴BA=CQ,PB=PC
∵PB=PC,
∴BP=PC=BC=7,
2t=7,
解得:t=,
CQ=BA=8,
v×=8,
解得:v=.
综上所述:当v=2或时,△ABP与△PQC全等.
2017年2月25日
一.选择题:(每小题4分,共40分)
1.4的平方根是( )
A.﹣2
B.2
C.±2
D.4
2.下列运算正确的是( )
A.(﹣3x)2=9x2
B.x x2=x2
C.(a3)2=9
D.a6÷a2=a3
3.下列命题是真命题的是( )
A.是无理数
B.﹣27没有立方根
C.相等的角是对顶角
D.全等三角形的对应边相等
4.下列各式由左边到右边的变形中,是因式分解的是( )
A.a2﹣3a+2=a(a﹣3)
B.a2x﹣a=a(ax﹣1)
C.x2+3x+9=(x+3)2
D.(x+1)(x﹣1)=x2﹣1
5.下列选项中,可用来说明命题“任何偶数都是8的倍数”是假命题的反例是( )
A.15
B.24
C.42
D.2k
6.如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( )
A.80°
B.60°
C.40°
D.20°
7.若x2+mx﹣15=(x+3)(x+n),则m的值是( )
A.﹣5
B.5
C.﹣2
D.2
8.若3x﹣2nym与xmy﹣3n的积与x4y3是同类项,则m+2n的立方根( )
A.﹣2
B.2
C.±2
D.8
9.若a﹣b=1,ab=4,则下列代数式a3b﹣2a2b2+ab3的值( )
A.3
B.4
C.5
D.6
10.如果一长方形的面积为2x2+x,它的一条边长为x,则它的周长为( )
A.2x+1
B.3x+1
C.6x+1
D.6x+2
二、填空题:(每小题4分,共40分)
11.设整数m满足﹣<m<,则m的个数是 .
12.命题“等角的余角相等”的条件是“两个角相等”,则结论是 .
13.如图,AC=AD,请你添加一个条件,根据“边角边”判定△ADB≌△ACB,你所添加的条件是 .
14.如果am=3,a2m+n=36,则an的值是 .
15.若a﹣b=1,则代数式a2﹣b2﹣2b的值为 .
16.已知a,b是△ABC的两边长,且满足a2﹣10a+=﹣25,则第三边c的取值范围是 .
三、解答题:
17.计算:
(1)(﹣1)2016+×+
(2)4x2 x+6x5y3÷(﹣3x2y3)
(3)(x+1)(x2﹣x+1)
(4)(2+a)(2﹣a)+(a+3)2.
18.因式分解:
(1)4x3﹣8x2+4x
(2)x2(a﹣1)+1﹣a.
19.化简求值:(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1),其中x,y的值满足y=+﹣1.
20.一个长方形活动场地的长为2am,宽比长少5m,实施“阳光体育”行动后,学校将长方形的长与宽都增加了4m,则
(1)扩大后长方形的宽为 m(用含a的代数式表示);
(2)求场地面积增加了多少m2?
21.如图,已知点E,C在线段BF上,AB=DE,AC=DF,∠A=∠D,
求证:(1)△ABC≌△DEF
(2)AB∥DE.
22.拼图与数学:
(1)如图1,观察左边方格图中阴影所示的图形(注:每一小方格的边长为1).若将它剪开,可重新拼成一个正方形,请你在右边的方格图中画出你所拼成的正方形,可用阴影增加效果,并写出你所拼成的正方形的边长 ;
(2)如图2是用4个相同的小长方形与1个正方形镶嵌而成的正方形图案.若用x、y表示小长方形的两边长(x>y),则请利用图中的面积关系直接写来代数式x+y、x﹣y、xy三者之间存在着等式关系: ;
(3)如图3,右图是2002年在北京召开的国际数学家大会的会标,它来源于我国古代著名的“赵爽弦图”.它是由4个全等的直角三角形(如左图,三边长分别为BC=a、AC=b、AB=c)及中间一个小正方形拼成的大正方形.请你利用图中的面积关系推导出一个有关直角三角形三边长a、b、c简洁的等量关系.
23.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
(1)用含a、b的代数式表示AE= ;
(2)若a+b=10,ab=20,求这两个正方形的面积之和;
(3)若a=10,△AFC的面积为S,则点E从点A向点B滑动的过程中,S的值是否会发生改变?若会,请说明理由;若不会,请求出S.
24.如图,在长方形ABCD中,AB=CD=8cm,BC=14cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)BP= cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
2016-2017学年福建省泉州市鹏峰中学八年级(上)期中数学试卷
参考答案与试题解析
一.选择题:(每小题4分,共40分)
1.4的平方根是( )
A.﹣2
B.2
C.±2
D.4
【考点】平方根.
【分析】首先根据平方根的定义求出4的平方根,然后就可以解决问题.
【解答】解:∵±2的平方等于4,
∴4的平方根是:±2.
故选C.
2.下列运算正确的是( )
A.(﹣3x)2=9x2
B.x x2=x2
C.(a3)2=9
D.a6÷a2=a3
【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.
【分析】结合同底数幂的除法、同底数幂的乘法、幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:A、(﹣3x)2=9x2,本选项正确;
B、x x2=x3≠x2,本选项错误;
C、(a3)2=a6≠a9,本选项错误;
D、a6÷a2=a4≠a3,本选项错误.
故选A.
3.下列命题是真命题的是( )
A.是无理数
B.﹣27没有立方根
C.相等的角是对顶角
D.全等三角形的对应边相等
【考点】命题与定理.
【分析】根据算术平方根的概念、立方根的概念、对顶角的定义、全等三角形的性质进行判断即可.
【解答】解:
=3是有理数,A错误;
﹣27的立方根是﹣3,B错误;
相等的角不一定是对顶角,C错误;
全等三角形的对应边相等,D正确,
故选:D.
4.下列各式由左边到右边的变形中,是因式分解的是( )
A.a2﹣3a+2=a(a﹣3)
B.a2x﹣a=a(ax﹣1)
C.x2+3x+9=(x+3)2
D.(x+1)(x﹣1)=x2﹣1
【考点】因式分解的意义.
【分析】利用因式分解的定义判断即可.
【解答】解:下列各式由左边到右边的变形中,是因式分解的是a2x﹣a=a(ax﹣1),
故选B
5.下列选项中,可用来说明命题“任何偶数都是8的倍数”是假命题的反例是( )
A.15
B.24
C.42
D.2k
【考点】命题与定理.
【分析】根据偶数与倍数的定义对各选项进行验证即可.
【解答】解:A、15不是偶数,故本选项错误;
B、24是8的倍数,故本选项错误;
C、42是偶数但不是8的倍数,故本选项正确;
D、2k是偶数,但不一定是8的倍数,故本选项错误;
故选C.
6.如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( )
A.80°
B.60°
C.40°
D.20°
【考点】全等三角形的性质.
【分析】根据三角形内角和定理可求∠ABC=60°,根据全等三角形的性质可证∠DCB=∠ABC,即可求∠DCB.
【解答】解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,∠ABC=∠DCB,
△ABC中,∠A=80°,∠ACB=40°,
∴∠ABC=180°﹣80°﹣40°=60°,
∴∠BCD=∠ABC=60°,
故选B.
7.若x2+mx﹣15=(x+3)(x+n),则m的值是( )
A.﹣5
B.5
C.﹣2
D.2
【考点】因式分解的意义.
【分析】把等式的右边展开得:x2+mx﹣15=x2+nx+3x+3n,然后根据对应项系数相等列式求解即可.
【解答】解:∵x2+mx﹣15=(x+3)(x+n),
∴x2+mx﹣15=x2+nx+3x+3n,
∴3n=﹣15,m=n+3,
解得n=﹣5,m=﹣5+3=﹣2.
故选C.
8.若3x﹣2nym与xmy﹣3n的积与x4y3是同类项,则m+2n的立方根( )
A.﹣2
B.2
C.±2
D.8
【考点】单项式乘单项式;立方根;同类项.
【分析】先依据单项式乘单项式法则计算,然后依据同类项的定义得到关于m、n的方程组,于是可求得m、n的值,然后再求得m+2n的值,最后求立方根即可.
【解答】解:3x﹣2nym xmy﹣3n=3xm﹣2nym﹣3n.
∵3x﹣2nym与xmy﹣3n的积与()4y3是同类项,
∴m﹣2n=4,m﹣3n=3,
解得n=1,m=6.
∴m+2n=8.
∴m+2n的立方根为2.
故选:B.
9.若a﹣b=1,ab=4,则下列代数式a3b﹣2a2b2+ab3的值( )
A.3
B.4
C.5
D.6
【考点】因式分解的应用.
【分析】提取公因式ab后再利用完全平方公式因式分解后整体代入即可求解.
【解答】解:a3b﹣2a2b2+ab3=ab(a﹣b)2=4×1=4.
故选:B.
10.如果一长方形的面积为2x2+x,它的一条边长为x,则它的周长为( )
A.2x+1
B.3x+1
C.6x+1
D.6x+2
【考点】整式的除法.
【分析】根据整式的除法,可得另一边长,根据整式的加法,可得答案.
【解答】解:另一边长为(2x2+x)÷x=2x+1,
周长为2[x+(2x+1)]=2(x+2x+1)=6x+2,
故选:D.
二、填空题:(每小题4分,共40分)
11.设整数m满足﹣<m<,则m的个数是 4 .
【考点】估算无理数的大小.
【分析】直接利用,的取值范围,进而得出符合题意的个数.
【解答】解:∵整数m满足﹣<m<,
∴m可以为:﹣1,0,1,2,
∴m的个数为4个.
故答案为:4.
12.命题“等角的余角相等”的条件是“两个角相等”,则结论是 它们的余角相等 .
【考点】命题与定理.
【分析】命题的已知部分是条件,即题设,由条件得出结果是结论.
【解答】解:“等角的余角相等”的条件是“两个角相等”,则结论是它们的余角相等;
故答案为:它们的余角相等.
13.如图,AC=AD,请你添加一个条件,根据“边角边”判定△ADB≌△ACB,你所添加的条件是 ∠CAB=∠DAB .
【考点】全等三角形的判定.
【分析】根据AC=AD,AB为公共边可知需要添加∠CAB=∠DAB.
【解答】解:在△ADB与△ACB中,
∵,
∴△ADB≌△ACB(SAS).
故答案为:∠CAB=∠DAB.
14.如果am=3,a2m+n=36,则an的值是 4 .
【考点】幂的乘方与积的乘方;同底数幂的乘法.
【分析】先将a2m+n变形为(am)2×an,然后结合幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:∵am=3,a2m+n=36=(am)2×an,
∴an
=a2m+n÷(am)2
=36÷32
=36÷9
=4.
故答案为:4.
15.若a﹣b=1,则代数式a2﹣b2﹣2b的值为 1 .
【考点】完全平方公式.
【分析】运用平方差公式,化简代入求值,
【解答】解:因为a﹣b=1,
a2﹣b2﹣2b=(a+b)(a﹣b)﹣2b=a+b﹣2b=a﹣b=1,
故答案为:1.
16.已知a,b是△ABC的两边长,且满足a2﹣10a+=﹣25,则第三边c的取值范围是 2<c<8 .
【考点】三角形三边关系.
【分析】已知等式左边前三项利用完全平方公式变形后,根据非负数的性质求出a与b的值,即可确定出c的范围.
【解答】解:∵a2﹣10a+25+=(a﹣5)2+=0,
∴a﹣5=0,b﹣3=0,即a=5,b=3,
则第三边c的取值范围是2<c<8.
故答案为:2<c<8.
三、解答题:
17.计算:
(1)(﹣1)2016+×+
(2)4x2 x+6x5y3÷(﹣3x2y3)
(3)(x+1)(x2﹣x+1)
(4)(2+a)(2﹣a)+(a+3)2.
【考点】整式的混合运算;实数的运算.
【分析】根据整式的混合运算法则、实数的性质解答即可.
【解答】解:(1)(﹣1)2016+×+=1﹣×5+2=1;
(2)4x2 x+6x5y3÷(﹣3x2y3)=10x3﹣2x3=8x3;
(3)(x+1)(x2﹣x+1)=x3﹣x2+x+x2﹣x+1=x3+1;
(4)(2+a)(2﹣a)+(a+3)2=4﹣a2+a2+6a+9=6a+13.
18.因式分解:
(1)4x3﹣8x2+4x
(2)x2(a﹣1)+1﹣a.
【考点】提公因式法与公式法的综合运用.
【分析】(1)先提公因式,然后利用完全平方公式分解因式;
(2)先提公因式,然后利用平方差公式分解因式.
【解答】解:(1)原式=4x(x2﹣2x+1)
=4x(x﹣1)2;
(2)原式=(a﹣1)(x2﹣1)
=(a﹣1)(x+1)(x﹣1).
19.化简求值:(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1),其中x,y的值满足y=+﹣1.
【考点】整式的混合运算—化简求值;二次根式有意义的条件.
【分析】先求出x、y的值,算乘法和除法,再合并同类项,最后代入求出即可.
【解答】解;∵x,y的值满足y=+﹣1,
∴x﹣3≥0且3﹣x≥0,
∴x=3,
∴y=﹣1,
(3x3y+2x2y2)÷xy+(x﹣y)2﹣(2x﹣1)(2x+1)
=3x2+2xy+x2﹣2xy+y2﹣4x2+1
=y2+1
=(﹣1)2+1
=2.
20.一个长方形活动场地的长为2am,宽比长少5m,实施“阳光体育”行动后,学校将长方形的长与宽都增加了4m,则
(1)扩大后长方形的宽为 2a﹣1 m(用含a的代数式表示);
(2)求场地面积增加了多少m2?
【考点】整式的混合运算.
【分析】(1)根据题意即可得到结论;
(2)根据矩形
面积公式即可得到结论.
【解答】解:(1)∵长方形活动场地的长为2am,宽比长少5m,
∴宽是2a﹣5,
∵将长方形的长与宽都增加了4m,
∴扩大后长方形的宽为2a﹣1,
故答案为:2a﹣1;
(2)(2a+4)(2a﹣1)﹣2a(2a﹣5)=16a﹣4m2,
∴场地面积增加了多少(16a﹣4)m2.
21.如图,已知点E,C在线段BF上,AB=DE,AC=DF,∠A=∠D,
求证:(1)△ABC≌△DEF
(2)AB∥DE.
【考点】全等三角形的判定与性质.
【分析】(1)根据SAS即可证明.
(2)利用全等三角形的性质可得∠B=∠DEC,由此可以推出AB∥DE.
【解答】证明:(1)在△BAC和△EDC中,
,
∴△BAC≌△EDC(SAS).
(2)∵△BAC≌△EDC,
∴∠B=∠EDC,
∴AB∥DE.
22.拼图与数学:
(1)如图1,观察左边方格图中阴影所示的图形(注:每一小方格的边长为1).若将它剪开,可重新拼成一个正方形,请你在右边的方格图中画出你所拼成的正方形,可用阴影增加效果,并写出你所拼成的正方形的边长 ;
(2)如图2是用4个相同的小长方形与1个正方形镶嵌而成的正方形图案.若用x、y表示小长方形的两边长(x>y),则请利用图中的面积关系直接写来代数式x+y、x﹣y、xy三者之间存在着等式关系: (x+y)2﹣4xy=(x﹣y)2 ;
(3)如图3,右图是2002年在北京召开的国际数学家大会的会标,它来源于我国古代著名的“赵爽弦图”.它是由4个全等的直角三角形(如左图,三边长分别为BC=a、AC=b、AB=c)及中间一个小正方形拼成的大正方形.请你利用图中的面积关系推导出一个有关直角三角形三边长a、b、c简洁的等量关系.
【考点】勾股定理的证明.
【分析】(1)根据正方形的面积求出边长,即可得解;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式x+y、x﹣y、xy之间的等量关系.
(3)先表示出中间小正方形的边长,然后根据大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积列出等式,然后整理即可得解.
【解答】解:(1)如图1所示:
(2)代数式x+y、x﹣y、xy三者之间存在着等式关系:(x+y)2﹣4xy=(x﹣y)2;
(3)它能说明的等式为:c2=a2+b2.
推导如下:中间小正方形的边长为(b﹣a),
∴大正方形的面积可表示为:
c2=4×ab+(b﹣a)2,
整理得,c2=2ab+b2﹣2ab+a2,
即c2=a2+b2.
故答案为:;(x+y)2﹣4xy=(x﹣y)2.
23.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连结AF、CF、AC.
(1)用含a、b的代数式表示AE= a﹣b ;
(2)若a+b=10,ab=20,求这两个正方形的面积之和;
(3)若a=10,△AFC的面积为S,则点E从点A向点B滑动的过程中,S的值是否会发生改变?若会,请说明理由;若不会,请求出S.
【考点】完全平方公式的几何背景.
【分析】(1)根据题意可知:AE=AB﹣BE=a﹣b;
(2)根据完全平方公式即可求出答案.
(3)设CF与AB交于点H,分别求出AH、EF、BC的长度即可求出S的值.
【解答】解:(1)AE=AB﹣BE=a﹣b
(2)∵(a+b)2=a2+2ab+b2,
∴这两个正方形的面积之和为:a2+b2=(a+b)2﹣2ab=100﹣40=60
(3)设CF与AB交于H,
∴BC=10,GB=GF=b,
∵BH∥GF,
∴△BCH∽△GCF
∴,
∴BH=,
∴AH=AB﹣BH=,
∴S=S△AFH+S△CHA
=AH GB+AH BC
=AH(GB+BC)
=AH GC
=××(10+b)
=50
∴S的值不会发生改变;
24.如图,在长方形ABCD中,AB=CD=8cm,BC=14cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)BP= 2t cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v
cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
【考点】四边形综合题.
【分析】(1)根据P点的运动速度可得BP的长;
(2)根据全等三角形的性质即可得出BP=CP即可;
(3)此题主要分两种情况①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
【解答】解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,
则PC=14﹣2t;
(2)当t=时,△ABP≌△DCP,
理由:∵BP=2t,CP=14﹣2t,
∵△ABP≌△DCP,
∴BP=CP,
∴2t=14﹣2t,
∴t=,
(2)①当△ABP≌△PCQ时,
∴BP=CQ,AB=PC,
∵AB=8,
∴PC=8,
∴BP=BC﹣PC=14﹣8=6,
2t=6,
解得:t=3,
CQ=BP=6,
v×3=6,
解得:v=2;
②当△ABP≌△QCP时,
∴BA=CQ,PB=PC
∵PB=PC,
∴BP=PC=BC=7,
2t=7,
解得:t=,
CQ=BA=8,
v×=8,
解得:v=.
综上所述:当v=2或时,△ABP与△PQC全等.
2017年2月25日
同课章节目录
