华师大版八年级下《第17章函数及图象》单元检测题含答案
文档属性
| 名称 | 华师大版八年级下《第17章函数及图象》单元检测题含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 221.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-27 00:00:00 | ||
图片预览

文档简介
华师大版八年级下册
第17章
函数及图象
单元检测题
1.函数y=中,自变量的取值范围是(
)
A.x>-2
B.x≥-2
C.x≠-2
D.x≤-2
2.一次函数y=-2x+1的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
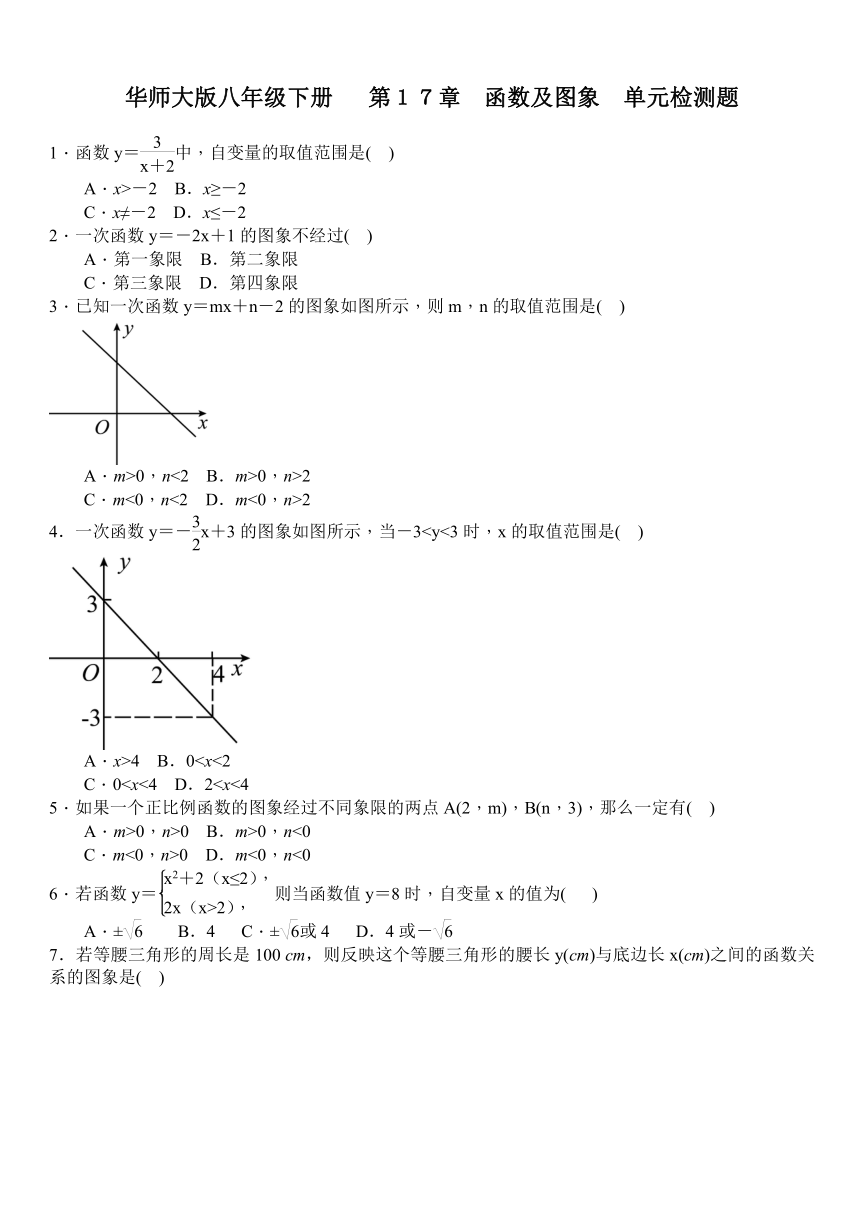
3.已知一次函数y=mx+n-2的图象如图所示,则m,n的取值范围是(
)
A.m>0,n<2
B.m>0,n>2
C.m<0,n<2
D.m<0,n>2
4.一次函数y=-x+3的图象如图所示,当-3)
A.x>4
B.0C.0D.25.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有(
)
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
6.若函数y=则当函数值y=8时,自变量x的值为(
)
A.±
B.4
C.±或4
D.4或-
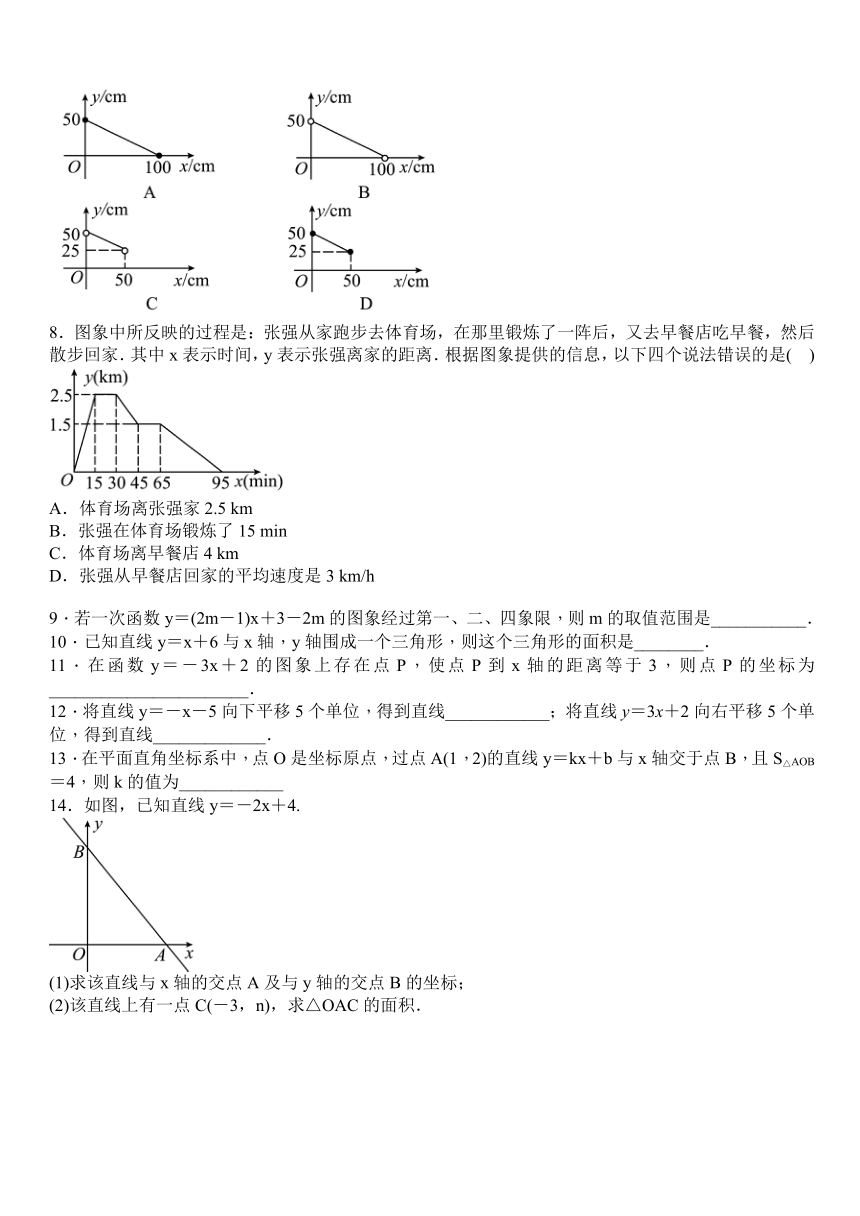
7.若等腰三角形的周长是100
cm,则反映这个等腰三角形的腰长y(cm)与底边长x(cm)之间的函数关系的图象是(
)
8.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是(
)
A.体育场离张强家2.5
km
B.张强在体育场锻炼了15
min
C.体育场离早餐店4
km
D.张强从早餐店回家的平均速度是3
km/h
9.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是___________.
10.已知直线y=x+6与x轴,y轴围成一个三角形,则这个三角形的面积是________.
11.在函数y=-3x+2的图象上存在点P,使点P到x轴的距离等于3,则点P的坐标为_______________________.
12.将直线y=-x-5向下平移5个单位,得到直线____________;将直线y=3x+2向右平移5个单位,得到直线_____________.
13.在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且S△AOB=4,则k的值为____________
14.如图,已知直线y=-2x+4.
(1)求该直线与x轴的交点A及与y轴的交点B的坐标;
(2)该直线上有一点C(-3,n),求△OAC的面积.
15.已知一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第三象限,它的横坐标为-2,△AOB的面积为6,求正比例函数和一次函数的表达式.
16.如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.
17.从甲地到乙地,先是一段平路,然后是一段上坡路.小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5
km,下坡的速度比平路上的速度每小时多5
km.设小明出发x
h后,到达离甲地y
km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为_______km/h;他途中休息了________h;
(2)求线段AB,BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15
h,那么该地点离甲地多远?
18.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2
h,并且甲车途中休息了0.5
h.如图是甲、乙两车行驶的路程y(km)与时间x(h)之间的函数图象.
(1)求出图中m,a的值;
(2)求出甲车行驶的路程y(km)与时间x(h)之间的函数表达式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50
km
答案:
1---8
CCDCD
DCC
9.
m<
10.
18
11.
(-,3)或(,-3)
12.
y=-x-10
y=3x-13
13.
-或
14.
解:(1)A(2,0),B(0,4)
(2)S△OAC=S△OBC+S△OBA=×4×3+×4×2=10
15.
解:∵S△AOB=×6·BD=6,∴BD=2,∴B(-2,-2).设正比例函数的表达式为y=k1x,一次函数的表达式为y=k2x+b,∴-2=-2k1,k1=1,∴解得∴正比例函数和一次函数的表达式分别为y=x和y=-x-3
16.
解:(1)由题意,得M(2,2).将M(2,2)代入y=-x+b,得b=3,∴y=-x+3.当y=0时,x=6,∴A(6,0)
(2)∵B(0,3),∴OB=CD=3,∴C(a,-a+3),D(a,a),∴CD=a-(-a+3)=3,a=4
17.
(1)
15
0.1
(2)yAB=10x+1.5(0.3≤x≤0.5),yBC=-20x+16.5(0.5≤x≤0.6)
(3)设小明第一次经过该地点的时间为t
h,则第二次经过该地点的时间为(t+0.15)h
,由题意,得10t+1.5=-20(t+0.15)+16.5,解得t=0.4,∴y=10×0.4+1.5=5.5.故该地点离甲地5.5
km
第17章
函数及图象
单元检测题
1.函数y=中,自变量的取值范围是(
)
A.x>-2
B.x≥-2
C.x≠-2
D.x≤-2
2.一次函数y=-2x+1的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.已知一次函数y=mx+n-2的图象如图所示,则m,n的取值范围是(
)
A.m>0,n<2
B.m>0,n>2
C.m<0,n<2
D.m<0,n>2
4.一次函数y=-x+3的图象如图所示,当-3
A.x>4
B.0
)
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
6.若函数y=则当函数值y=8时,自变量x的值为(
)
A.±
B.4
C.±或4
D.4或-
7.若等腰三角形的周长是100
cm,则反映这个等腰三角形的腰长y(cm)与底边长x(cm)之间的函数关系的图象是(
)
8.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是(
)
A.体育场离张强家2.5
km
B.张强在体育场锻炼了15
min
C.体育场离早餐店4
km
D.张强从早餐店回家的平均速度是3
km/h
9.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是___________.
10.已知直线y=x+6与x轴,y轴围成一个三角形,则这个三角形的面积是________.
11.在函数y=-3x+2的图象上存在点P,使点P到x轴的距离等于3,则点P的坐标为_______________________.
12.将直线y=-x-5向下平移5个单位,得到直线____________;将直线y=3x+2向右平移5个单位,得到直线_____________.
13.在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且S△AOB=4,则k的值为____________
14.如图,已知直线y=-2x+4.
(1)求该直线与x轴的交点A及与y轴的交点B的坐标;
(2)该直线上有一点C(-3,n),求△OAC的面积.
15.已知一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第三象限,它的横坐标为-2,△AOB的面积为6,求正比例函数和一次函数的表达式.
16.如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.
17.从甲地到乙地,先是一段平路,然后是一段上坡路.小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5
km,下坡的速度比平路上的速度每小时多5
km.设小明出发x
h后,到达离甲地y
km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为_______km/h;他途中休息了________h;
(2)求线段AB,BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15
h,那么该地点离甲地多远?
18.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2
h,并且甲车途中休息了0.5
h.如图是甲、乙两车行驶的路程y(km)与时间x(h)之间的函数图象.
(1)求出图中m,a的值;
(2)求出甲车行驶的路程y(km)与时间x(h)之间的函数表达式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50
km
答案:
1---8
CCDCD
DCC
9.
m<
10.
18
11.
(-,3)或(,-3)
12.
y=-x-10
y=3x-13
13.
-或
14.
解:(1)A(2,0),B(0,4)
(2)S△OAC=S△OBC+S△OBA=×4×3+×4×2=10
15.
解:∵S△AOB=×6·BD=6,∴BD=2,∴B(-2,-2).设正比例函数的表达式为y=k1x,一次函数的表达式为y=k2x+b,∴-2=-2k1,k1=1,∴解得∴正比例函数和一次函数的表达式分别为y=x和y=-x-3
16.
解:(1)由题意,得M(2,2).将M(2,2)代入y=-x+b,得b=3,∴y=-x+3.当y=0时,x=6,∴A(6,0)
(2)∵B(0,3),∴OB=CD=3,∴C(a,-a+3),D(a,a),∴CD=a-(-a+3)=3,a=4
17.
(1)
15
0.1
(2)yAB=10x+1.5(0.3≤x≤0.5),yBC=-20x+16.5(0.5≤x≤0.6)
(3)设小明第一次经过该地点的时间为t
h,则第二次经过该地点的时间为(t+0.15)h
,由题意,得10t+1.5=-20(t+0.15)+16.5,解得t=0.4,∴y=10×0.4+1.5=5.5.故该地点离甲地5.5
km
