中考数学压轴题解法探究(4)—动态几何定值问题
文档属性
| 名称 | 中考数学压轴题解法探究(4)—动态几何定值问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 965.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览




文档简介
中考数学压轴题解法探讨
动态几何定值问题
【专题解析】
考题研究:
数学因运动而充满活力,数学因变化而精彩纷呈。动态题是近年来中考的的一个热点问题,以运动的观点探究几何图形的变化规律问题,称之为动态几何问题,随之产生的动态几何试题就是研究在几何图形的运动中,伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题,就其运动对象而言,有点动、线动、面动三大类,就其运动形式而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等,就问题类型而言,有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。解这类题目要 “以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。以动态几何问题为基架而精心设计的考题,可谓璀璨夺目、精彩四射。2·1·c·n·j·y
解题攻略:
动态几何形成的定值和恒等问题是动态几何中的常见问题,其考点包括线段(和差)为定值问题;角度(和差)为定值问题;面积(和差)为定值问题;其它定值问题。【来源:21·世纪·教育·网】
解答动态几何定值问题的方法,一般有两种:
第一种是分两步完成 :先探求定值. 它要用题中固有的几何量表示.再证明它能成立.探求的方法,常用特殊位置定值法,即把动点放在特殊的位置,找出定值的表达式,然后写出证明.
第二种是采用综合法,直接写出证明.
解题思路:
在中考中,动态几何形成的定值和恒等问题命题形式主要为解答题。在中考压轴题中,动态几何之定值(恒等)问题的重点是线段(和差)为定值问题,问题的难点在于准确应用适当的定理和方法进行探究。2-1-c-n-j-y
【真题精讲】
类型一:与线段、角等相关的定值问题
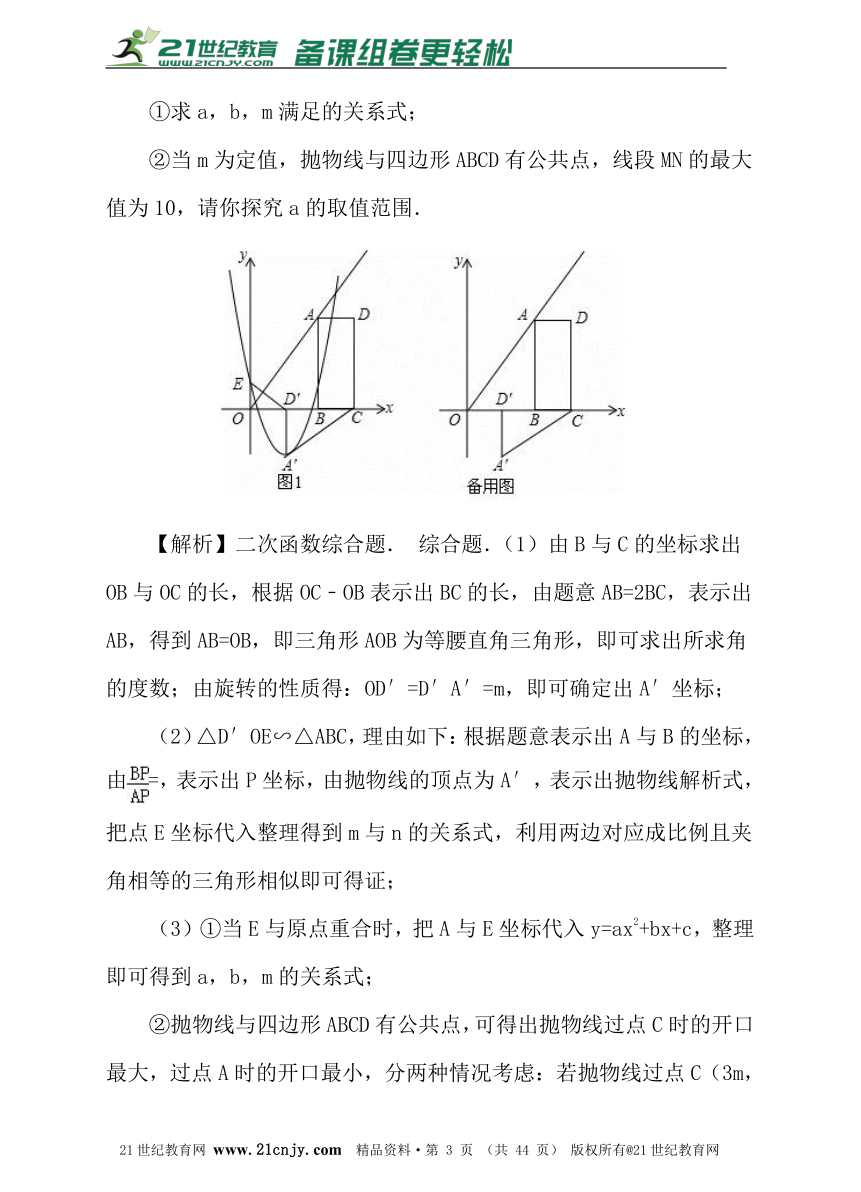
典例1:(2015?宜昌,第24题12分)如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.21教育名师原创作品
(1)填空:∠AOB= 45 °,用m表示点A′的坐标:A′( m , ﹣m );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且=时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
【解析】二次函数综合题. 综合题.(1)由B与C的坐标求出OB与OC的长,根据OC﹣OB表示出BC的长,由题意AB=2BC,表示出AB,得到AB=OB,即三角形AOB为等腰直角三角形,即可求出所求角的度数;由旋转的性质得:OD′=D′A′=m,即可确定出A′坐标;
(2)△D′OE∽△ABC,理由如下:根据题意表示出A与B的坐标,由=,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入整理得到m与n的关系式,利用两边对应成比例且夹角相等的三角形相似即可得证;
(3)①当E与原点重合时,把A与E坐标代入y=ax2+bx+c,整理即可得到a,b,m的关系式;
②抛物线与四边形ABCD有公共点,可得出抛物线过点C时的开口最大,过点A时的开口最小,分两种情况考虑:若抛物线过点C(3m,0),此时MN的最大值为10,求出此时a的值;若抛物线过点A(2m,2m),求出此时a的值,即可确定出抛物线与四边形ABCD有公共点时a的范围.
【解答】解:(1)∵B(2m,0),C(3m,0),
∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,﹣m);
故答案为:45;m,﹣m;
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵=,
∴P(2m,m),
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x﹣m)2﹣m,
∵抛物线过点E(0,n),
∴n=a(0﹣m)2﹣m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+c过点E,A,
∴,
整理得:am+b=﹣1,即b=﹣1﹣am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为10,
∴a(3m)2﹣(1+am)?3m=0,
整理得:am=,即抛物线解析式为y=x2﹣x,
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得:,
解得:x=5m,y=5m,即M(5m,5m),
令5m=10,即m=2,
当m=2时,a=;
若抛物线过点A(2m,2m),则a(2m)2﹣(1+am)?2m=2m,
解得:am=2,
∵m=2,
∴a=1,
则抛物线与四边形ABCD有公共点时a的范围为≤a≤1.
【点评】此题属于二次函数综合题,涉及的知识有:坐标与图形性质,等腰直角三角形的判定与性质,直线与抛物线的交点,以及二次函数的图象与性质,熟练掌握二次函数的性质是解本题的关键.
变式训练1:
(2015?辽宁省盘锦,第26题14分)如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
类型二:与面积相关的定值问题
典例2:(2016·青海西宁·12分)如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分.【来源:21cnj*y.co*m】
(1)求过A,B,E三点的抛物线的解析式;
(2)求证:四边形AMCD是菱形;
(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由.
【解析】二次函数综合题.(1)根据题意首先求出抛物线顶点E的坐标,再利用顶点式求出函数解析式;
(2)利用等边三角形的性质结合圆的有关性质得出∠AMD=∠CMD=∠AMC=60°,进而得出DC=CM=MA=AD,即可得出答案;
(3)首先表示出△ABP的面积进而求出n的值,再代入函数关系式求出P点坐标.
【解答】(1)解:由题意可知,△MBC为等边三角形,点A,B,C,E均在⊙M上,
则MA=MB=MC=ME=2,
又∵CO⊥MB,
∴MO=BO=1,
∴A(﹣3,0),B(1,0),E(﹣1,﹣2),
抛物线顶点E的坐标为(﹣1,﹣2),
设函数解析式为y=a(x+1)2﹣2(a≠0)
把点B(1,0)代入y=a(x+1)2﹣2,
解得:a=,
故二次函数解析式为:y=(x+1)2﹣2;
(2)证明:连接DM,
∵△MBC为等边三角形,
∴∠CMB=60°,
∴∠AMC=120°,
∵点D平分弧AC,
∴∠AMD=∠CMD=∠AMC=60°,
∵MD=MC=MA,
∴△MCD,△MDA是等边三角形,
∴DC=CM=MA=AD,
∴四边形AMCD为菱形(四条边都相等的四边形是菱形);
(3)解:存在.
理由如下:
设点P的坐标为(m,n)
∵S△ABP=AB|n|,AB=4
∴×4×|n|=5,
即2|n|=5,
解得:n=±,
当时,(m+1)2﹣2=,
解此方程得:m1=2,m2=﹣4
即点P的坐标为(2,),(﹣4,),
当n=﹣时,(m+1)2﹣2=﹣,
此方程无解,
故所求点P坐标为(2,),(﹣4,).
变式训练2:
(黄石市2016年)本小题满分10分)已知二次函数
(1)当时,函数值随的增大而减小,求的取值范围。
(2)以抛物线的顶点为一个顶点作该抛物线的内接正三角形(,两点在抛物线上),请问:△的面积是与无关的定值吗?若是,请求出这个定值;若不是,请说明理由。21cnjy.com
(3)若抛物线与轴交点的横坐标均为整数,求整数的值。
类型三:与比例相关的定值问题
典例3:(2016·湖北武汉·12分)抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.21·世纪*教育网
【考点】二次函数综合;考查了待定系数法求函数解析式;平行线的判定;函数值相等的点关于对称轴对称。
【答案】 (1)①y=x2-;②点D的坐标为(-1,-3)或(,);(2)是定值,等于2
【解析】解:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
,解得 ,抛物线的解析式为: .
②如图:
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为 ,再联立 得:x=1或 ,∴ D2( )21*cnjy*com
∴点D的坐标为(-1,-3)或( )
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=,过点P(x0,y0)作PH⊥AB,有,易证:△PAH∽△EAO,则 即,∴,
同理得∴,∴,则OE+OF=
∴,又OC=-c,∴.
∴是定值,等于2.
变式训练3:
(2016·浙江省湖州市)数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数t,则t= .
【过关检测】
1. (2015?甘肃天水,第9题,4分)如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )www-2-1-cnjy-com
A. B.
C. D.
2. (2015江苏苏州,28,12分)如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1﹣S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
3. (2014?连云港,第27题14分)某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
【解析】四边形综合题(1)设AP=x,则PB=1﹣x,根据正方形的面积公式得到这两个正方形面积之和=x2+(8﹣x)2,配方得到2(x﹣4)2+32,然后根据二次函数的最值问题求解.
(2)根据PE∥BF求得PK=,进而求得DK=PD﹣PK=a﹣=,然后根据面积公式即可求得.
(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;
(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
4. (2015?永州,第27题10分)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).21*cnjy*com
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
【参考答案】
变式训练参考答案:
变式训练1:
(2015?辽宁省盘锦,第26题14分)如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.21教育网
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【解析】二次函数综合题.(1)利用待定系数法求得即可;
(2)根据C的纵坐标求得F的坐标,然后通过△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,根据圆周角定理求得∠ECF=∠EDF,由于tan∠ECF===,即可求得tan∠FDE=;
②连接CE,得出△CDE是等腰直角三角形,得出∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为y=﹣x+3,即可设出直线DG1的解析式为y=﹣x+m,直线DG2的解析式为y=2x+n,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
【解答】解:(1)如图1,∵抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,
∴,
解得.
∴抛物线解析式为y=﹣x2+x+3;
(2)如图2,∵点F恰好在抛物线上,C(0,3),
∴F的纵坐标为3,
把y=3代入y=﹣x2+x+3得,3=﹣x2+x+3;
解得x=0或x=4,
∴F(4,3),
∴OH=4,
∵∠CDE=90°,
∴∠ODC+∠EDH=90°,
∴∠OCD=∠EDH,
在△OCD和△HDE中,
,
∴△OCD≌△HDE(AAS),
∴DH=OC=3,
∴OD=4﹣3=1;
(3)①如图3,连接CE,
∵△OCD≌△HDE,
∴HE=OD=1,
∵BF=OC=3,
∴EF=3﹣1=2,
∵∠CDE=∠CFE=90°,
∴C、D、E、F四点共圆,
∴∠ECF=∠EDF,
在RT△CEF中,∵CF=OH=4,
∴tan∠ECF===,
∴tan∠FDE=;
②如图4,连接CE,
∵CD=DE,∠CDE=90°,
∴∠CED=45°,
过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°【出处:21教育名师】
∵EH=1,OH=4,
∴E(4,1),
∵C(0,3),
∴直线CE的解析式为y=﹣x+3,
设直线DG1的解析式为y=﹣x+m,
∵D(1,0),
∴0=﹣×1+m,解得m=,
∴直线DG1的解析式为y=﹣x+,
当x=4时,y=﹣+=﹣,
∴G1(4,﹣);
设直线DG2的解析式为y=2x+n,
∵D(1,0),
∴0=2×1+n,解得n=﹣2,
∴直线DG2的解析式为y=2x﹣2,
当x=4时,y=2×4﹣2=6,
∴G2(4,6);
综上,在直线l上,是否存在点G,使∠EDG=45°,点G的坐标为(4,﹣)或(4,6).
【点评】本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,一次函数的解析式,三角形全等的判定和性质,等腰直角三角形的性质,平行线的性质等,数形结合思想的应用是解题的关键.【版权所有:21教育】
变式训练2:
(黄石市2016年)本小题满分10分)已知二次函数
(1)当时,函数值随的增大而减小,求的取值范围。
(2)以抛物线的顶点为一个顶点作该抛物线的内接正三角形(,两点在抛物线上),请问:△的面积是与无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线与轴交点的横坐标均为整数,求整数的值。
【解析】
【解答】解:(1)∵
∴由题意得,
(2)根据抛物线和正三角形的对称性,可知轴,设抛物线的对称轴与交于点,则。设
∴
又
∴ ∴
∴,
∴定值 (3分)
(3)令,即时,有
由题意,为完全平方数,令
即
∵为整数, ∴的奇偶性相同
∴或
解得或
综合得
变式训练3:
(2016·浙江省湖州市)数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数t,则t= .
【解析】几何变换综合题.(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.
(2)设DH=x,由由题意,CD=2x,CH=x,由△ACE∽△HCF,得=由此即可证明.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得=,由AB?CM=AD?CN,AD=3AB,推出CM=3CN,所以==,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
【解答】解;(1)①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)设DH=x,由由题意,CD=2x,CH=x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC==2x,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴==2,
∴AE=2FH.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴=,
∵AB?CM=AD?CN,AD=3AB,
∴CM=3CN,
∴==,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=a,HN=a,
∴AM=a,AH=a,
∴AC==a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=a,21·cn·jy·com
∴==.
故答案为.
过关检测参考答案:
1. (2015?甘肃天水,第9题,4分)如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
C. D.
【解析】动点问题的函数图象.根据弦CD为定长可以知道无论点C怎么运动弦CD的弦心距为定值,据此可以得到函数的图象.
【解答】解:作OH⊥CD于点H,
∴H为CD的中点,
∵CF⊥CD交AB于F,DE⊥CD交AB于E,
∴OH为直角梯形的中位线,
∵弦CD为定长,
∴CF+DE=y为定值,
故选B.
【点评】本题考查了动点问题的函数图象,解题的关键是化动为静.
2. (2015江苏苏州,28,12分)如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1﹣S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
【解析】(1)根据题意表示出AG、GD的长度,再由△GCD∽△APG,利用对应边成比例可解出x的值.
(2)利用(1)得出的y与x的关系式表示出S1、S2,然后作差即可.
(3)延长PD交AC于点Q,然后判断△DGP是等腰直角三角形,从而结合x的范围得出x的值,在Rt△DGP中,解直角三角形可得出PD的长度.
【解答】解:(1)∵CG∥AP,
∴△GCD∽△APG,
∴=,
∵GF=4,CD=DA=1,AF=x,
∴GD=3﹣x,AG=4﹣x,
∴=,即y=,
∴y关于x的函数关系式为y=,
当y=3时,=3,解得x=2.5,
经检验的x=2.5是分式方程的根.
故x的值为2.5;
(2)∵S1=GP?GD=??(3﹣x)=,
S2=GD?CD=(3﹣x)1=,
∴S1﹣S2=﹣=即为常数;
(3)延长PD交AC于点Q.
∵正方形ABCD中,AC为对角线,
∴∠CAD=45°,
∵PQ⊥AC,
∴∠ADQ=45°,
∴∠GDP=∠ADQ=45°.
∴△DGP是等腰直角三角形,则GD=GP,
∴3﹣x=,
化简得:x2﹣5x+5=0.
解得:x=,
∵0≤x≤2.5,
∴x=,
在Rt△DGP中,PD==(3﹣x)=.
【点评】此题考查了正方形的性质、等腰三角形的性质及解直角三角形的知识,解答本题的关键是用移动的时间表示出有关线段的长度,然后运用所学知识进行求解.
3. (2014?连云港,第27题14分)某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.www.21-cn-jy.com
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
【解析】四边形综合题(1)设AP=x,则PB=1﹣x,根据正方形的面积公式得到这两个正方形面积之和=x2+(8﹣x)2,配方得到2(x﹣4)2+32,然后根据二次函数的最值问题求解.
(2)根据PE∥BF求得PK=,进而求得DK=PD﹣PK=a﹣=,然后根据面积公式即可求得.
(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;
(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
【解答】解:(1)当点P运动时,这两个正方形的面积之和不是定值.
设AP=x,则PB=8﹣x,
根据题意得这两个正方形面积之和=x2+(8﹣x)2
=2x2﹣16x+64
=2(x﹣4)2+32,
所以当x=4时,这两个正方形面积之和有最小值,最小值为32.
(2)存在两个面积始终相等的三角形,它们是△APK与△DFK.
依题意画出图形,如答图2所示.
设AP=a,则PB=BF=8﹣a.
∵PE∥BF,
∴,即,
∴PK=,
∴DK=PD﹣PK=a﹣=,
∴S△APK=PK?PA=??a=,S△DFK=DK?EF=?(8﹣a)=,
∴S△APK=S△DFK.
(3)当点P从点A出发,沿A→B→C→D的线路,向点D运动时,不妨设点Q在DA边上,
若点P在点A,点Q在点D,此时PQ的中点O即为DA边的中点;
若点Q在DA边上,且不在点D,则点P在AB上,且不在点A.
此时在Rt△APQ中,O为PQ的中点,所以AO=PQ=4.
所以点O在以A为圆心,半径为4,圆心角为90°的圆弧上.
PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如下图所示:
所以PQ的中点O所经过的路径的长为:×2π×4=6π.
(4)点O所经过的路径长为3,OM+OB的最小值为.
如答下图,分别过点G、O、H作AB的垂线,垂足分别为点R、S、T,则四边形GRTH为梯形.
∵点O为中点,
∴OS=(GR+HT)=(AP+PB)=4,即OS为定值.
∴点O的运动路径在与AB距离为4的平行线上.
∵MN=6,点P在线段MN上运动,且点O为GH中点,
∴点O的运动路径为线段XY,XY=MN=3,XY∥AB且平行线之间距离为4,点X与点A、点Y与点B之间的水平距离均为2.5.
如答下图,作点M关于直线XY的对称点M′,连接BM′,与XY交于点O.
由轴对称性质可知,此时OM+OB=BM′最小.
在Rt△BMM′中,由勾股定理得:BM′==.
∴OM+OB的最小值为.
【点评】本题是中考压轴题,难度较大.解题难点在于分析动点的运动轨迹,需要很好的空间想象能力和作图分析能力;此外本题还综合考查了二次函数、整式运算、四边形、中位线、相似、轴对称与勾股定理等众多知识点,是一道好题.
4. (2015?永州,第27题10分)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
【解析】圆的综合题.探究型.(1)如图一,易证∠PMO+∠PNO=180°,从而可得四边形PMON内接于圆,直径OP=2;
(2)如图一,易证四边形PMON是矩形,则有MN=OP=2,问题得以解决;
(3)①如图二,根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°,根据圆内接四边形的对角互补可得∠MP1N=60°.根据角平分线的性质可得P1M=P1N,从而得到△P1MN是等边三角形,则有MN=P1M.然后在Rt△P1MO运用三角函数就可解决问题;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,根据圆周角定理可得∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中运用三角函数可得:MN=QN?sin∠MQN,从而可得MN=OP?sin∠MQN,由此即可解决问题;
(4)由(3)②中已得结论MN=OP?sin∠MQN可知,当∠MQN=90°时,MN最大,问题得以解决.
【解答】解:(1)如图一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四边形PMON内接于圆,直径OP=2;
(2)如图一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∴MN的长为定值,该定值为2;
(3)①如图二,
∵P1是的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,
∴△P1MN是等边三角形,
∴MN=P1M.
∵P1M=OP1?sin∠MOP1=2×sin60°= ,
∴MN= ;
②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,
则有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN=,
∴MN=QN?sin∠MQN,
∴MN=OP?sin∠MQN=2×sin60°=2×= ,
∴MN是定值.
(4)由(3)②得MN=OP?sin∠MQN=2sin∠MQN.
当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.
【点评】本题主要考查了圆内接四边形的判定定理、圆周角定理、在同圆中弧与圆心角的关系、矩形的判定与性质、等边三角形的判定与性质、三角函数、角平分线的性质等知识,推出MN=OP?sin∠MQN是解决本题的关键.21世纪教育网版权所有
动态几何定值问题
【专题解析】
考题研究:
数学因运动而充满活力,数学因变化而精彩纷呈。动态题是近年来中考的的一个热点问题,以运动的观点探究几何图形的变化规律问题,称之为动态几何问题,随之产生的动态几何试题就是研究在几何图形的运动中,伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题,就其运动对象而言,有点动、线动、面动三大类,就其运动形式而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等,就问题类型而言,有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。解这类题目要 “以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。以动态几何问题为基架而精心设计的考题,可谓璀璨夺目、精彩四射。2·1·c·n·j·y
解题攻略:
动态几何形成的定值和恒等问题是动态几何中的常见问题,其考点包括线段(和差)为定值问题;角度(和差)为定值问题;面积(和差)为定值问题;其它定值问题。【来源:21·世纪·教育·网】
解答动态几何定值问题的方法,一般有两种:
第一种是分两步完成 :先探求定值. 它要用题中固有的几何量表示.再证明它能成立.探求的方法,常用特殊位置定值法,即把动点放在特殊的位置,找出定值的表达式,然后写出证明.
第二种是采用综合法,直接写出证明.
解题思路:
在中考中,动态几何形成的定值和恒等问题命题形式主要为解答题。在中考压轴题中,动态几何之定值(恒等)问题的重点是线段(和差)为定值问题,问题的难点在于准确应用适当的定理和方法进行探究。2-1-c-n-j-y
【真题精讲】
类型一:与线段、角等相关的定值问题
典例1:(2015?宜昌,第24题12分)如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.21教育名师原创作品
(1)填空:∠AOB= 45 °,用m表示点A′的坐标:A′( m , ﹣m );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且=时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
【解析】二次函数综合题. 综合题.(1)由B与C的坐标求出OB与OC的长,根据OC﹣OB表示出BC的长,由题意AB=2BC,表示出AB,得到AB=OB,即三角形AOB为等腰直角三角形,即可求出所求角的度数;由旋转的性质得:OD′=D′A′=m,即可确定出A′坐标;
(2)△D′OE∽△ABC,理由如下:根据题意表示出A与B的坐标,由=,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入整理得到m与n的关系式,利用两边对应成比例且夹角相等的三角形相似即可得证;
(3)①当E与原点重合时,把A与E坐标代入y=ax2+bx+c,整理即可得到a,b,m的关系式;
②抛物线与四边形ABCD有公共点,可得出抛物线过点C时的开口最大,过点A时的开口最小,分两种情况考虑:若抛物线过点C(3m,0),此时MN的最大值为10,求出此时a的值;若抛物线过点A(2m,2m),求出此时a的值,即可确定出抛物线与四边形ABCD有公共点时a的范围.
【解答】解:(1)∵B(2m,0),C(3m,0),
∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,﹣m);
故答案为:45;m,﹣m;
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵=,
∴P(2m,m),
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x﹣m)2﹣m,
∵抛物线过点E(0,n),
∴n=a(0﹣m)2﹣m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+c过点E,A,
∴,
整理得:am+b=﹣1,即b=﹣1﹣am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为10,
∴a(3m)2﹣(1+am)?3m=0,
整理得:am=,即抛物线解析式为y=x2﹣x,
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得:,
解得:x=5m,y=5m,即M(5m,5m),
令5m=10,即m=2,
当m=2时,a=;
若抛物线过点A(2m,2m),则a(2m)2﹣(1+am)?2m=2m,
解得:am=2,
∵m=2,
∴a=1,
则抛物线与四边形ABCD有公共点时a的范围为≤a≤1.
【点评】此题属于二次函数综合题,涉及的知识有:坐标与图形性质,等腰直角三角形的判定与性质,直线与抛物线的交点,以及二次函数的图象与性质,熟练掌握二次函数的性质是解本题的关键.
变式训练1:
(2015?辽宁省盘锦,第26题14分)如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
类型二:与面积相关的定值问题
典例2:(2016·青海西宁·12分)如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分.【来源:21cnj*y.co*m】
(1)求过A,B,E三点的抛物线的解析式;
(2)求证:四边形AMCD是菱形;
(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由.
【解析】二次函数综合题.(1)根据题意首先求出抛物线顶点E的坐标,再利用顶点式求出函数解析式;
(2)利用等边三角形的性质结合圆的有关性质得出∠AMD=∠CMD=∠AMC=60°,进而得出DC=CM=MA=AD,即可得出答案;
(3)首先表示出△ABP的面积进而求出n的值,再代入函数关系式求出P点坐标.
【解答】(1)解:由题意可知,△MBC为等边三角形,点A,B,C,E均在⊙M上,
则MA=MB=MC=ME=2,
又∵CO⊥MB,
∴MO=BO=1,
∴A(﹣3,0),B(1,0),E(﹣1,﹣2),
抛物线顶点E的坐标为(﹣1,﹣2),
设函数解析式为y=a(x+1)2﹣2(a≠0)
把点B(1,0)代入y=a(x+1)2﹣2,
解得:a=,
故二次函数解析式为:y=(x+1)2﹣2;
(2)证明:连接DM,
∵△MBC为等边三角形,
∴∠CMB=60°,
∴∠AMC=120°,
∵点D平分弧AC,
∴∠AMD=∠CMD=∠AMC=60°,
∵MD=MC=MA,
∴△MCD,△MDA是等边三角形,
∴DC=CM=MA=AD,
∴四边形AMCD为菱形(四条边都相等的四边形是菱形);
(3)解:存在.
理由如下:
设点P的坐标为(m,n)
∵S△ABP=AB|n|,AB=4
∴×4×|n|=5,
即2|n|=5,
解得:n=±,
当时,(m+1)2﹣2=,
解此方程得:m1=2,m2=﹣4
即点P的坐标为(2,),(﹣4,),
当n=﹣时,(m+1)2﹣2=﹣,
此方程无解,
故所求点P坐标为(2,),(﹣4,).
变式训练2:
(黄石市2016年)本小题满分10分)已知二次函数
(1)当时,函数值随的增大而减小,求的取值范围。
(2)以抛物线的顶点为一个顶点作该抛物线的内接正三角形(,两点在抛物线上),请问:△的面积是与无关的定值吗?若是,请求出这个定值;若不是,请说明理由。21cnjy.com
(3)若抛物线与轴交点的横坐标均为整数,求整数的值。
类型三:与比例相关的定值问题
典例3:(2016·湖北武汉·12分)抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.21·世纪*教育网
【考点】二次函数综合;考查了待定系数法求函数解析式;平行线的判定;函数值相等的点关于对称轴对称。
【答案】 (1)①y=x2-;②点D的坐标为(-1,-3)或(,);(2)是定值,等于2
【解析】解:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
,解得 ,抛物线的解析式为: .
②如图:
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为 ,再联立 得:x=1或 ,∴ D2( )21*cnjy*com
∴点D的坐标为(-1,-3)或( )
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=,过点P(x0,y0)作PH⊥AB,有,易证:△PAH∽△EAO,则 即,∴,
同理得∴,∴,则OE+OF=
∴,又OC=-c,∴.
∴是定值,等于2.
变式训练3:
(2016·浙江省湖州市)数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数t,则t= .
【过关检测】
1. (2015?甘肃天水,第9题,4分)如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )www-2-1-cnjy-com
A. B.
C. D.
2. (2015江苏苏州,28,12分)如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1﹣S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
3. (2014?连云港,第27题14分)某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
【解析】四边形综合题(1)设AP=x,则PB=1﹣x,根据正方形的面积公式得到这两个正方形面积之和=x2+(8﹣x)2,配方得到2(x﹣4)2+32,然后根据二次函数的最值问题求解.
(2)根据PE∥BF求得PK=,进而求得DK=PD﹣PK=a﹣=,然后根据面积公式即可求得.
(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;
(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
4. (2015?永州,第27题10分)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).21*cnjy*com
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
【参考答案】
变式训练参考答案:
变式训练1:
(2015?辽宁省盘锦,第26题14分)如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.21教育网
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【解析】二次函数综合题.(1)利用待定系数法求得即可;
(2)根据C的纵坐标求得F的坐标,然后通过△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,根据圆周角定理求得∠ECF=∠EDF,由于tan∠ECF===,即可求得tan∠FDE=;
②连接CE,得出△CDE是等腰直角三角形,得出∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为y=﹣x+3,即可设出直线DG1的解析式为y=﹣x+m,直线DG2的解析式为y=2x+n,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
【解答】解:(1)如图1,∵抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,
∴,
解得.
∴抛物线解析式为y=﹣x2+x+3;
(2)如图2,∵点F恰好在抛物线上,C(0,3),
∴F的纵坐标为3,
把y=3代入y=﹣x2+x+3得,3=﹣x2+x+3;
解得x=0或x=4,
∴F(4,3),
∴OH=4,
∵∠CDE=90°,
∴∠ODC+∠EDH=90°,
∴∠OCD=∠EDH,
在△OCD和△HDE中,
,
∴△OCD≌△HDE(AAS),
∴DH=OC=3,
∴OD=4﹣3=1;
(3)①如图3,连接CE,
∵△OCD≌△HDE,
∴HE=OD=1,
∵BF=OC=3,
∴EF=3﹣1=2,
∵∠CDE=∠CFE=90°,
∴C、D、E、F四点共圆,
∴∠ECF=∠EDF,
在RT△CEF中,∵CF=OH=4,
∴tan∠ECF===,
∴tan∠FDE=;
②如图4,连接CE,
∵CD=DE,∠CDE=90°,
∴∠CED=45°,
过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°【出处:21教育名师】
∵EH=1,OH=4,
∴E(4,1),
∵C(0,3),
∴直线CE的解析式为y=﹣x+3,
设直线DG1的解析式为y=﹣x+m,
∵D(1,0),
∴0=﹣×1+m,解得m=,
∴直线DG1的解析式为y=﹣x+,
当x=4时,y=﹣+=﹣,
∴G1(4,﹣);
设直线DG2的解析式为y=2x+n,
∵D(1,0),
∴0=2×1+n,解得n=﹣2,
∴直线DG2的解析式为y=2x﹣2,
当x=4时,y=2×4﹣2=6,
∴G2(4,6);
综上,在直线l上,是否存在点G,使∠EDG=45°,点G的坐标为(4,﹣)或(4,6).
【点评】本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,一次函数的解析式,三角形全等的判定和性质,等腰直角三角形的性质,平行线的性质等,数形结合思想的应用是解题的关键.【版权所有:21教育】
变式训练2:
(黄石市2016年)本小题满分10分)已知二次函数
(1)当时,函数值随的增大而减小,求的取值范围。
(2)以抛物线的顶点为一个顶点作该抛物线的内接正三角形(,两点在抛物线上),请问:△的面积是与无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线与轴交点的横坐标均为整数,求整数的值。
【解析】
【解答】解:(1)∵
∴由题意得,
(2)根据抛物线和正三角形的对称性,可知轴,设抛物线的对称轴与交于点,则。设
∴
又
∴ ∴
∴,
∴定值 (3分)
(3)令,即时,有
由题意,为完全平方数,令
即
∵为整数, ∴的奇偶性相同
∴或
解得或
综合得
变式训练3:
(2016·浙江省湖州市)数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数t,则t= .
【解析】几何变换综合题.(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.
(2)设DH=x,由由题意,CD=2x,CH=x,由△ACE∽△HCF,得=由此即可证明.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得=,由AB?CM=AD?CN,AD=3AB,推出CM=3CN,所以==,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
【解答】解;(1)①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)设DH=x,由由题意,CD=2x,CH=x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC==2x,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴==2,
∴AE=2FH.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴=,
∵AB?CM=AD?CN,AD=3AB,
∴CM=3CN,
∴==,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=a,HN=a,
∴AM=a,AH=a,
∴AC==a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=a,21·cn·jy·com
∴==.
故答案为.
过关检测参考答案:
1. (2015?甘肃天水,第9题,4分)如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
C. D.
【解析】动点问题的函数图象.根据弦CD为定长可以知道无论点C怎么运动弦CD的弦心距为定值,据此可以得到函数的图象.
【解答】解:作OH⊥CD于点H,
∴H为CD的中点,
∵CF⊥CD交AB于F,DE⊥CD交AB于E,
∴OH为直角梯形的中位线,
∵弦CD为定长,
∴CF+DE=y为定值,
故选B.
【点评】本题考查了动点问题的函数图象,解题的关键是化动为静.
2. (2015江苏苏州,28,12分)如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1﹣S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
【解析】(1)根据题意表示出AG、GD的长度,再由△GCD∽△APG,利用对应边成比例可解出x的值.
(2)利用(1)得出的y与x的关系式表示出S1、S2,然后作差即可.
(3)延长PD交AC于点Q,然后判断△DGP是等腰直角三角形,从而结合x的范围得出x的值,在Rt△DGP中,解直角三角形可得出PD的长度.
【解答】解:(1)∵CG∥AP,
∴△GCD∽△APG,
∴=,
∵GF=4,CD=DA=1,AF=x,
∴GD=3﹣x,AG=4﹣x,
∴=,即y=,
∴y关于x的函数关系式为y=,
当y=3时,=3,解得x=2.5,
经检验的x=2.5是分式方程的根.
故x的值为2.5;
(2)∵S1=GP?GD=??(3﹣x)=,
S2=GD?CD=(3﹣x)1=,
∴S1﹣S2=﹣=即为常数;
(3)延长PD交AC于点Q.
∵正方形ABCD中,AC为对角线,
∴∠CAD=45°,
∵PQ⊥AC,
∴∠ADQ=45°,
∴∠GDP=∠ADQ=45°.
∴△DGP是等腰直角三角形,则GD=GP,
∴3﹣x=,
化简得:x2﹣5x+5=0.
解得:x=,
∵0≤x≤2.5,
∴x=,
在Rt△DGP中,PD==(3﹣x)=.
【点评】此题考查了正方形的性质、等腰三角形的性质及解直角三角形的知识,解答本题的关键是用移动的时间表示出有关线段的长度,然后运用所学知识进行求解.
3. (2014?连云港,第27题14分)某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.www.21-cn-jy.com
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
【解析】四边形综合题(1)设AP=x,则PB=1﹣x,根据正方形的面积公式得到这两个正方形面积之和=x2+(8﹣x)2,配方得到2(x﹣4)2+32,然后根据二次函数的最值问题求解.
(2)根据PE∥BF求得PK=,进而求得DK=PD﹣PK=a﹣=,然后根据面积公式即可求得.
(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;
(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
【解答】解:(1)当点P运动时,这两个正方形的面积之和不是定值.
设AP=x,则PB=8﹣x,
根据题意得这两个正方形面积之和=x2+(8﹣x)2
=2x2﹣16x+64
=2(x﹣4)2+32,
所以当x=4时,这两个正方形面积之和有最小值,最小值为32.
(2)存在两个面积始终相等的三角形,它们是△APK与△DFK.
依题意画出图形,如答图2所示.
设AP=a,则PB=BF=8﹣a.
∵PE∥BF,
∴,即,
∴PK=,
∴DK=PD﹣PK=a﹣=,
∴S△APK=PK?PA=??a=,S△DFK=DK?EF=?(8﹣a)=,
∴S△APK=S△DFK.
(3)当点P从点A出发,沿A→B→C→D的线路,向点D运动时,不妨设点Q在DA边上,
若点P在点A,点Q在点D,此时PQ的中点O即为DA边的中点;
若点Q在DA边上,且不在点D,则点P在AB上,且不在点A.
此时在Rt△APQ中,O为PQ的中点,所以AO=PQ=4.
所以点O在以A为圆心,半径为4,圆心角为90°的圆弧上.
PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如下图所示:
所以PQ的中点O所经过的路径的长为:×2π×4=6π.
(4)点O所经过的路径长为3,OM+OB的最小值为.
如答下图,分别过点G、O、H作AB的垂线,垂足分别为点R、S、T,则四边形GRTH为梯形.
∵点O为中点,
∴OS=(GR+HT)=(AP+PB)=4,即OS为定值.
∴点O的运动路径在与AB距离为4的平行线上.
∵MN=6,点P在线段MN上运动,且点O为GH中点,
∴点O的运动路径为线段XY,XY=MN=3,XY∥AB且平行线之间距离为4,点X与点A、点Y与点B之间的水平距离均为2.5.
如答下图,作点M关于直线XY的对称点M′,连接BM′,与XY交于点O.
由轴对称性质可知,此时OM+OB=BM′最小.
在Rt△BMM′中,由勾股定理得:BM′==.
∴OM+OB的最小值为.
【点评】本题是中考压轴题,难度较大.解题难点在于分析动点的运动轨迹,需要很好的空间想象能力和作图分析能力;此外本题还综合考查了二次函数、整式运算、四边形、中位线、相似、轴对称与勾股定理等众多知识点,是一道好题.
4. (2015?永州,第27题10分)问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
【解析】圆的综合题.探究型.(1)如图一,易证∠PMO+∠PNO=180°,从而可得四边形PMON内接于圆,直径OP=2;
(2)如图一,易证四边形PMON是矩形,则有MN=OP=2,问题得以解决;
(3)①如图二,根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°,根据圆内接四边形的对角互补可得∠MP1N=60°.根据角平分线的性质可得P1M=P1N,从而得到△P1MN是等边三角形,则有MN=P1M.然后在Rt△P1MO运用三角函数就可解决问题;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,根据圆周角定理可得∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中运用三角函数可得:MN=QN?sin∠MQN,从而可得MN=OP?sin∠MQN,由此即可解决问题;
(4)由(3)②中已得结论MN=OP?sin∠MQN可知,当∠MQN=90°时,MN最大,问题得以解决.
【解答】解:(1)如图一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四边形PMON内接于圆,直径OP=2;
(2)如图一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∴MN的长为定值,该定值为2;
(3)①如图二,
∵P1是的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,
∴△P1MN是等边三角形,
∴MN=P1M.
∵P1M=OP1?sin∠MOP1=2×sin60°= ,
∴MN= ;
②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,
则有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN=,
∴MN=QN?sin∠MQN,
∴MN=OP?sin∠MQN=2×sin60°=2×= ,
∴MN是定值.
(4)由(3)②得MN=OP?sin∠MQN=2sin∠MQN.
当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.
【点评】本题主要考查了圆内接四边形的判定定理、圆周角定理、在同圆中弧与圆心角的关系、矩形的判定与性质、等边三角形的判定与性质、三角函数、角平分线的性质等知识,推出MN=OP?sin∠MQN是解决本题的关键.21世纪教育网版权所有
同课章节目录
