26.1.2反比例函数的图象和性质的综合应用 同步练习
文档属性
| 名称 | 26.1.2反比例函数的图象和性质的综合应用 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 22:01:43 | ||
图片预览



文档简介
26.1.4 反比例函数的图象和性质的综合应用
基础训练
知识点1 几何图形的面积与反比例函数解析式的关系
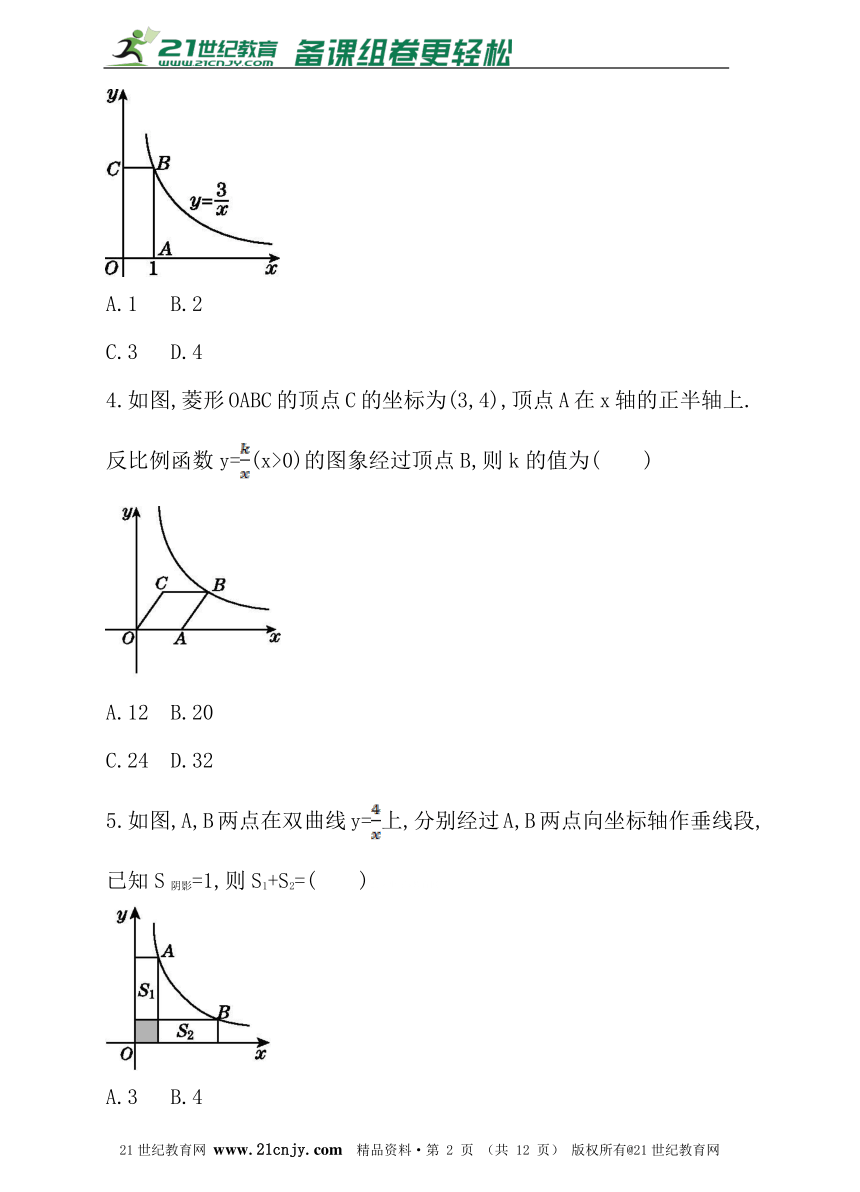
1.如图,已知A点是反比例函数y=(k≠0,x>0)的图象上一点,AB⊥x轴于B,且△ABO的面积为5,则k的值为_______________.?
2.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=(x<0)的图象经过点C,则k的值为_______________.21·cn·jy·com
3.如图,点B在反比例函数y=(x>0)的图象上,过B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )21cnjy.com
A.1 B.2
C.3 D.4
4.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( )
A.12 B.20
C.24 D.32
5.如图,A,B两点在双曲线y=上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=( )21·世纪*教育网
A.3 B.4
C.5 D.6
知识点2 反比例函数图象和性质的综合应用
6.下列关于反比例函数y=的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,y随x的增大而减小;③它的图象在第二、四象限内.其中正确的是_____________.www-2-1-cnjy-com
7.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(-2,-1)两点,若y1A.x<1 B.x<-2
C.-21 D.x<-2或08.函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是( )
A.y= B.y=
C.y= D.y=
9.直线y=kx(k>0)与双曲线y=交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为( )【来源:21cnj*y.co*m】
A.-8 B.4 C.-4 D.0
10.若反比例函数y=与一次函数y=x+3的图象有交点,则m的值不可以是( )
A.-3 B.-1
C.1 D.2
11.如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为 .【出处:21教育名师】
提升训练
考查角度1利用点的坐标与解析式的关系求坐标与解析式
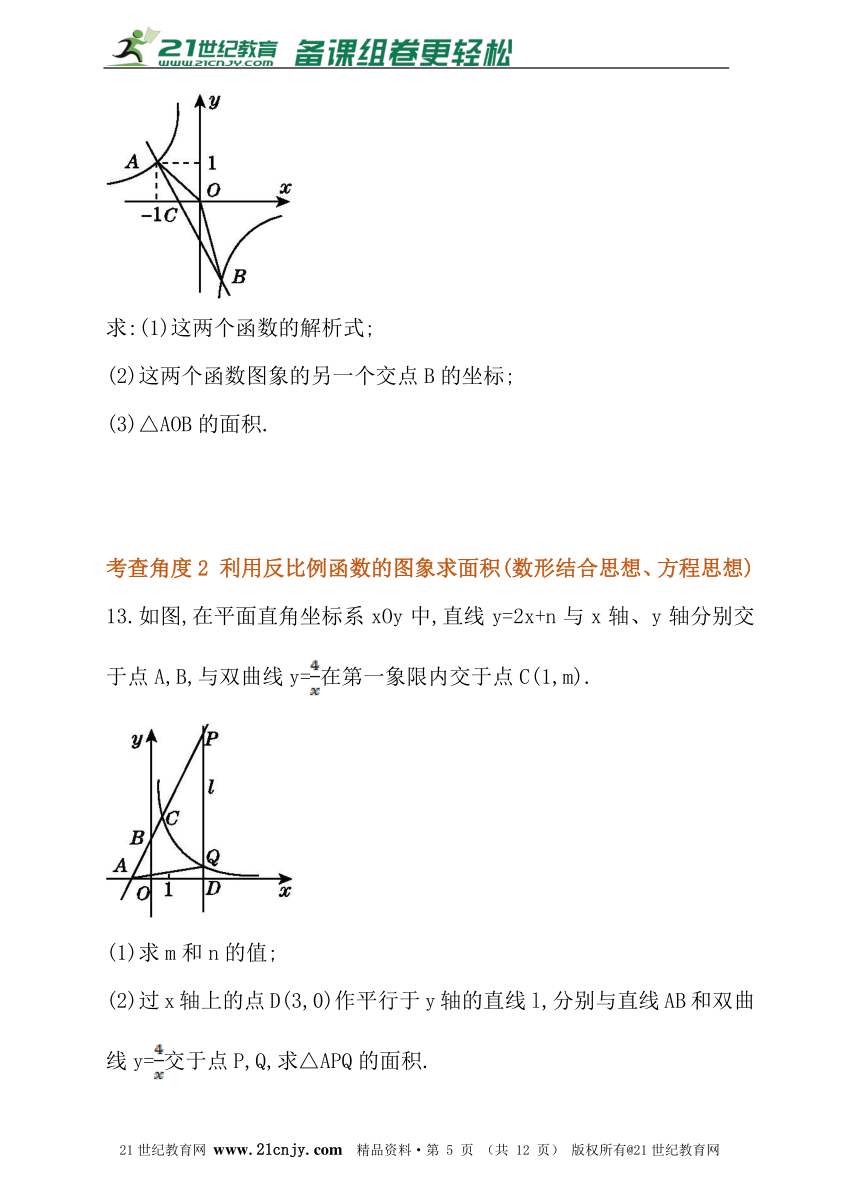
12.已知反比例函数y=和一次函数y=mx-1的图象交于点A(-1,1),B(n,-2),且一次函数图象交x轴于点C,如图所示.
求:(1)这两个函数的解析式;
(2)这两个函数图象的另一个交点B的坐标;
(3)△AOB的面积.
考查角度2 利用反比例函数的图象求面积(数形结合思想、方程思想)
13.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A,B,与双曲线y=在第一象限内交于点C(1,m).
(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线y=交于点P,Q,求△APQ的面积.21世纪教育网版权所有
考查角度3 利用反比例函数的图象和性质解与几何相关的问题(数形结合思想)
14.如图,在平面直角坐标系中,点A是反比例函数y1=的图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点;一次函数y2=ax+b的图象经过A,C两点,并交y轴于点D(0,-2),若S△AOD=4.21教育网
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请指出在y轴的右侧,当y1>y2时,x的取值范围.
15.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B两点.www.21-cn-jy.com
(1)求反比例函数的解析式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
16.如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(1,2).
(1)求反比例函数的解析式;
(2)根据图象直接写出当mx>时,x的取值范围;
(3)计算线段AB的长.
17.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.2·1·c·n·j·y
(1)求一次函数的解析式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
参考答案
1.【答案】10 2.【答案】-6 3.【答案】C
4.【答案】D 5.【答案】D
6.【答案】①② 7.【答案】D 8.【答案】A
9.【答案】C 10.【答案】A
11.【答案】y=-
解:函数图象往往蕴涵若干重要条件,这一点容易被忽略.本题由给出的图象可知反比例函数的比例系数k小于0.【来源:21·世纪·教育·网】
12.解:(1)把点A(-1,1)的坐标分别代入反比例函数y=和一次函数y=mx-1中,得1=,1=-m-1,解得k=-2,m=-2.【版权所有:21教育】
所以这两个函数的解析式分别为y=-和y=-2x-1.
(2)将点B(n,-2)的坐标代入y=-,得-2=-,所以n=,所以另一个交点B的坐标为.
(3)由一次函数y=-2x-1的图象交x轴于点C,得点C的坐标为.
所以S△AOB=S△AOC+S△BOC
=×1×+×|-2|×
=.
13.解:(1)把(1,m)代入y=中,得m=.解得m=4.
∴点C的坐标为(1,4).
把(1,4)代入y=2x+n,得4=2×1+n,解得n=2.
(2)对于y=2x+2,令x=3,则y=2×3+2=8,
∴点P的坐标为(3,8).
令y=0,则2x+2=0,即x=-1,
∴点A的坐标为(-1,0).
对于y=,令x=3,则y=.
∴点Q的坐标为.
∴△APQ的面积=AD·PQ=×(3+1)×=.
分析:注意反比例函数与一次函数图象的交点坐标满足两个函数的解析式,解答这类题通常运用方程思想.
14.解:(1)过A点作AE⊥y轴于点E.
∵S△AOD=4,OD=2,∴OD·AE=4.∴AE=4.
∵AB⊥OB,点C为OB的中点,
∴∠DOC=∠ABC=90°,OC=BC.
又∵∠OCD=∠BCA,
∴Rt△DOC≌Rt△ABC.
∴AB=OD=2,∴A(4,2).
将A(4,2)的坐标代入y1=中,得k=8.
∴y1=.
将A(4,2)和D(0,-2)的坐标分别代入y2=ax+b中,
得解得
∴y2=x-2.
(2)观察图象可得,在y轴的右侧,当y1>y2时,0技巧解:这是一道数形结合问题,是几何图形结合反比例函数、一次函数图象性质的综合题,解决此类题目的关键是抓住数与形之间的转化,特别是点的坐标与线段长度间的转化.21*cnjy*com
15.解:(1)由已知可得,a=-1+4=3,k=1×a=1×3=3,
∴反比例函数的解析式为y=.
联立 解得 或 所以B(3,1).
(2)如图所示,作B点关于x轴的对称点,得到B'(3,-1),
连接AB'交x轴于点P',连接P'B,则有PA+PB=PA+PB'≥AB',当P点和P'点重合时取等号.易得直线AB'的解析式为y=-2x+5.令y=0,
得x=,∴P',即满足条件的点P的坐标为.
设函数y=-x+4的图象交x轴于点C,则C(4,0),
∴S△PAB=S△APC-S△BPC=×PC×(yA-yB), 即S△PAB=××(3-1)=.
16.分析:(1)将A(1,2)的坐标代入y=即可求得反比例函数的解析式.(2)由直线y=mx与双曲线y=的特点可知点A,B关于原点O对称,从而可知B(-1,-2),从而x的取值范围可得.(3)由点A的坐标求出线段OA的长,利用AB=2OA可求线段AB的长,或利用点A,B的坐标直接求线段AB的长.2-1-c-n-j-y
解:(1)把A(1,2)的坐标代入y=中,得k=2.
∴反比例函数的解析式为y=.
(2)-11.
(3)过点A作AC⊥x轴,垂足为点C.
∵A(1,2),∴AC=2,OC=1.
∴OA==.
∴AB=2OA=2.
17.解:(1)将A(-2,b)的坐标分别代入y=kx+5,y=-可得b=-2k+5,b=-.
∴b=4,k=.
∴一次函数的解析式为y=x+5.
(2)将直线AB向下平移m个单位长度后,直线为y=x+5-m.联立y=x+5-m与y=-,得整理,得x2+(5-m)x+8=0.
∵直线y=x+5-m与反比例函数y=-的图象有且只有一个公共点,
∴Δ=(5-m)2-4××8=0,解得m=1或m=9,
即m的值为1或9.
基础训练
知识点1 几何图形的面积与反比例函数解析式的关系
1.如图,已知A点是反比例函数y=(k≠0,x>0)的图象上一点,AB⊥x轴于B,且△ABO的面积为5,则k的值为_______________.?
2.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=(x<0)的图象经过点C,则k的值为_______________.21·cn·jy·com
3.如图,点B在反比例函数y=(x>0)的图象上,过B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )21cnjy.com
A.1 B.2
C.3 D.4
4.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( )
A.12 B.20
C.24 D.32
5.如图,A,B两点在双曲线y=上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=( )21·世纪*教育网
A.3 B.4
C.5 D.6
知识点2 反比例函数图象和性质的综合应用
6.下列关于反比例函数y=的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,y随x的增大而减小;③它的图象在第二、四象限内.其中正确的是_____________.www-2-1-cnjy-com
7.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(-2,-1)两点,若y1
C.-2
A.y= B.y=
C.y= D.y=
9.直线y=kx(k>0)与双曲线y=交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为( )【来源:21cnj*y.co*m】
A.-8 B.4 C.-4 D.0
10.若反比例函数y=与一次函数y=x+3的图象有交点,则m的值不可以是( )
A.-3 B.-1
C.1 D.2
11.如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为 .【出处:21教育名师】
提升训练
考查角度1利用点的坐标与解析式的关系求坐标与解析式
12.已知反比例函数y=和一次函数y=mx-1的图象交于点A(-1,1),B(n,-2),且一次函数图象交x轴于点C,如图所示.
求:(1)这两个函数的解析式;
(2)这两个函数图象的另一个交点B的坐标;
(3)△AOB的面积.
考查角度2 利用反比例函数的图象求面积(数形结合思想、方程思想)
13.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A,B,与双曲线y=在第一象限内交于点C(1,m).
(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线y=交于点P,Q,求△APQ的面积.21世纪教育网版权所有
考查角度3 利用反比例函数的图象和性质解与几何相关的问题(数形结合思想)
14.如图,在平面直角坐标系中,点A是反比例函数y1=的图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点;一次函数y2=ax+b的图象经过A,C两点,并交y轴于点D(0,-2),若S△AOD=4.21教育网
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请指出在y轴的右侧,当y1>y2时,x的取值范围.
15.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B两点.www.21-cn-jy.com
(1)求反比例函数的解析式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
16.如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(1,2).
(1)求反比例函数的解析式;
(2)根据图象直接写出当mx>时,x的取值范围;
(3)计算线段AB的长.
17.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.2·1·c·n·j·y
(1)求一次函数的解析式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
参考答案
1.【答案】10 2.【答案】-6 3.【答案】C
4.【答案】D 5.【答案】D
6.【答案】①② 7.【答案】D 8.【答案】A
9.【答案】C 10.【答案】A
11.【答案】y=-
解:函数图象往往蕴涵若干重要条件,这一点容易被忽略.本题由给出的图象可知反比例函数的比例系数k小于0.【来源:21·世纪·教育·网】
12.解:(1)把点A(-1,1)的坐标分别代入反比例函数y=和一次函数y=mx-1中,得1=,1=-m-1,解得k=-2,m=-2.【版权所有:21教育】
所以这两个函数的解析式分别为y=-和y=-2x-1.
(2)将点B(n,-2)的坐标代入y=-,得-2=-,所以n=,所以另一个交点B的坐标为.
(3)由一次函数y=-2x-1的图象交x轴于点C,得点C的坐标为.
所以S△AOB=S△AOC+S△BOC
=×1×+×|-2|×
=.
13.解:(1)把(1,m)代入y=中,得m=.解得m=4.
∴点C的坐标为(1,4).
把(1,4)代入y=2x+n,得4=2×1+n,解得n=2.
(2)对于y=2x+2,令x=3,则y=2×3+2=8,
∴点P的坐标为(3,8).
令y=0,则2x+2=0,即x=-1,
∴点A的坐标为(-1,0).
对于y=,令x=3,则y=.
∴点Q的坐标为.
∴△APQ的面积=AD·PQ=×(3+1)×=.
分析:注意反比例函数与一次函数图象的交点坐标满足两个函数的解析式,解答这类题通常运用方程思想.
14.解:(1)过A点作AE⊥y轴于点E.
∵S△AOD=4,OD=2,∴OD·AE=4.∴AE=4.
∵AB⊥OB,点C为OB的中点,
∴∠DOC=∠ABC=90°,OC=BC.
又∵∠OCD=∠BCA,
∴Rt△DOC≌Rt△ABC.
∴AB=OD=2,∴A(4,2).
将A(4,2)的坐标代入y1=中,得k=8.
∴y1=.
将A(4,2)和D(0,-2)的坐标分别代入y2=ax+b中,
得解得
∴y2=x-2.
(2)观察图象可得,在y轴的右侧,当y1>y2时,0
15.解:(1)由已知可得,a=-1+4=3,k=1×a=1×3=3,
∴反比例函数的解析式为y=.
联立 解得 或 所以B(3,1).
(2)如图所示,作B点关于x轴的对称点,得到B'(3,-1),
连接AB'交x轴于点P',连接P'B,则有PA+PB=PA+PB'≥AB',当P点和P'点重合时取等号.易得直线AB'的解析式为y=-2x+5.令y=0,
得x=,∴P',即满足条件的点P的坐标为.
设函数y=-x+4的图象交x轴于点C,则C(4,0),
∴S△PAB=S△APC-S△BPC=×PC×(yA-yB), 即S△PAB=××(3-1)=.
16.分析:(1)将A(1,2)的坐标代入y=即可求得反比例函数的解析式.(2)由直线y=mx与双曲线y=的特点可知点A,B关于原点O对称,从而可知B(-1,-2),从而x的取值范围可得.(3)由点A的坐标求出线段OA的长,利用AB=2OA可求线段AB的长,或利用点A,B的坐标直接求线段AB的长.2-1-c-n-j-y
解:(1)把A(1,2)的坐标代入y=中,得k=2.
∴反比例函数的解析式为y=.
(2)-1
(3)过点A作AC⊥x轴,垂足为点C.
∵A(1,2),∴AC=2,OC=1.
∴OA==.
∴AB=2OA=2.
17.解:(1)将A(-2,b)的坐标分别代入y=kx+5,y=-可得b=-2k+5,b=-.
∴b=4,k=.
∴一次函数的解析式为y=x+5.
(2)将直线AB向下平移m个单位长度后,直线为y=x+5-m.联立y=x+5-m与y=-,得整理,得x2+(5-m)x+8=0.
∵直线y=x+5-m与反比例函数y=-的图象有且只有一个公共点,
∴Δ=(5-m)2-4××8=0,解得m=1或m=9,
即m的值为1或9.
