27.2.1 平行线截三角形相似定理 同步练习
文档属性
| 名称 | 27.2.1 平行线截三角形相似定理 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 612.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 22:20:41 | ||
图片预览

文档简介
27.2.2 平行线截三角形相似定理
基础训练
知识点1 平行线截三角形相似定理
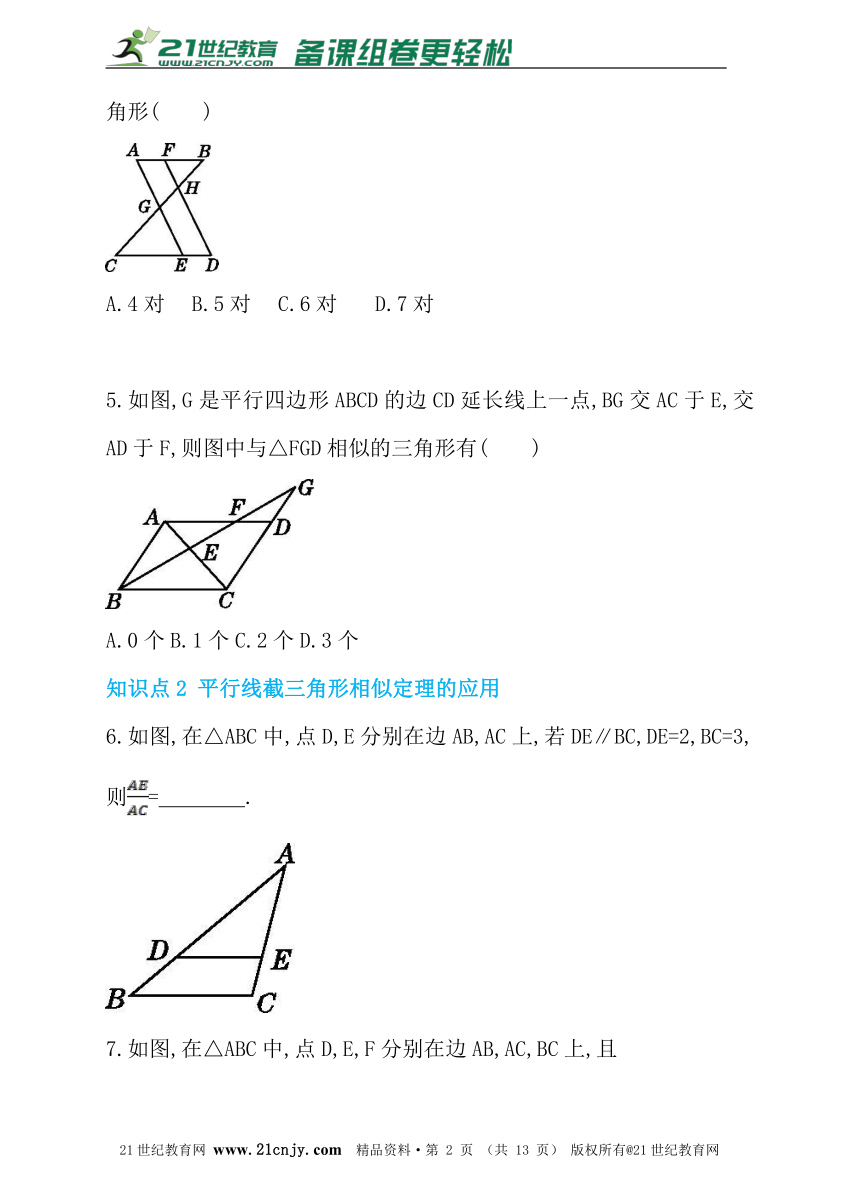
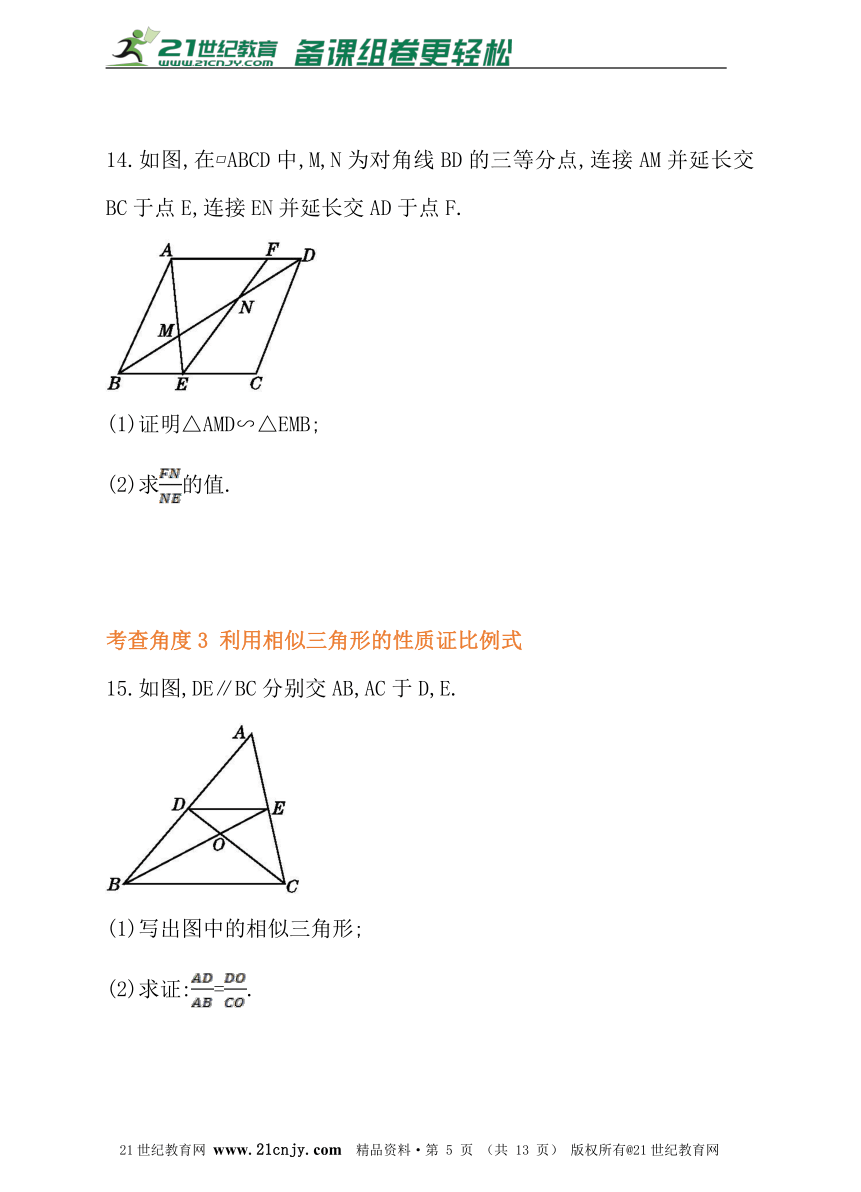
1.如图,E为平行四边形ABCD的边BC延长线上一点,连接AE,交边CD于点F.在不添加辅助线的情况下,请写出图中一对相似三角形: .?21cnjy.com
2.如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出所有与△BEF相似的三角形: .www-2-1-cnjy-com
3.如图,在△ABC中,EF∥BC,DG∥AB,EF和DG相交于点H,则图中与△ABC相似的三角形共有( )21*cnjy*com
A.1个 B.2个 C.3个 D.4个
4.如图,AB∥CD,AE∥FD,AE,FD分别交BC于点G,H,则图中共有相似三角形( )
A.4对 B.5对 C.6对 D.7对
5.如图,G是平行四边形ABCD的边CD延长线上一点,BG交AC于E,交AD于F,则图中与△FGD相似的三角形有( )【来源:21cnj*y.co*m】
A.0个 B.1个 C.2个 D.3个
知识点2 平行线截三角形相似定理的应用
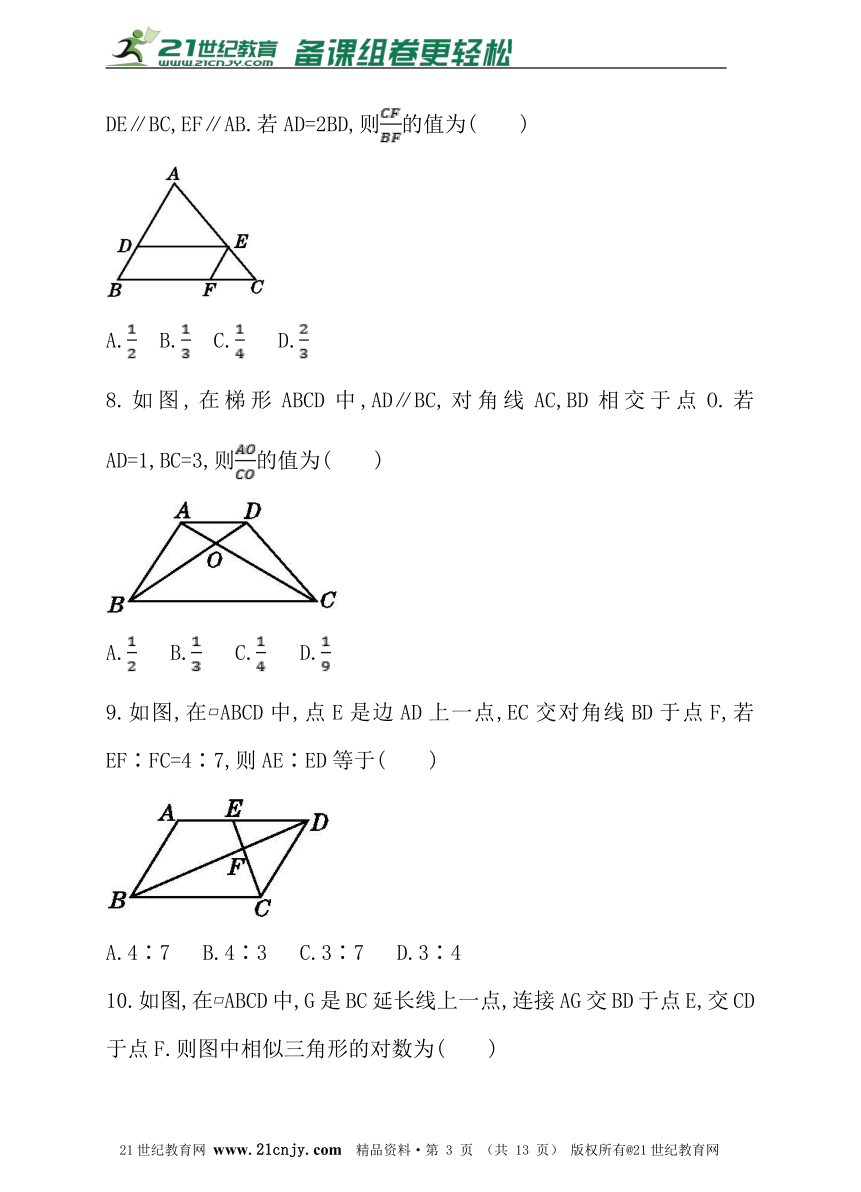
6.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,则= .【版权所有:21教育】
7.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且
DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A. B. C. D.
8.如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若AD=1,BC=3,则的值为( )21教育名师原创作品
A. B. C. D.
9.如图,在?ABCD中,点E是边AD上一点,EC交对角线BD于点F,若EF∶FC=4∶7,则AE∶ED等于( )21*cnjy*com
A.4∶7 B.4∶3 C.3∶7 D.3∶4
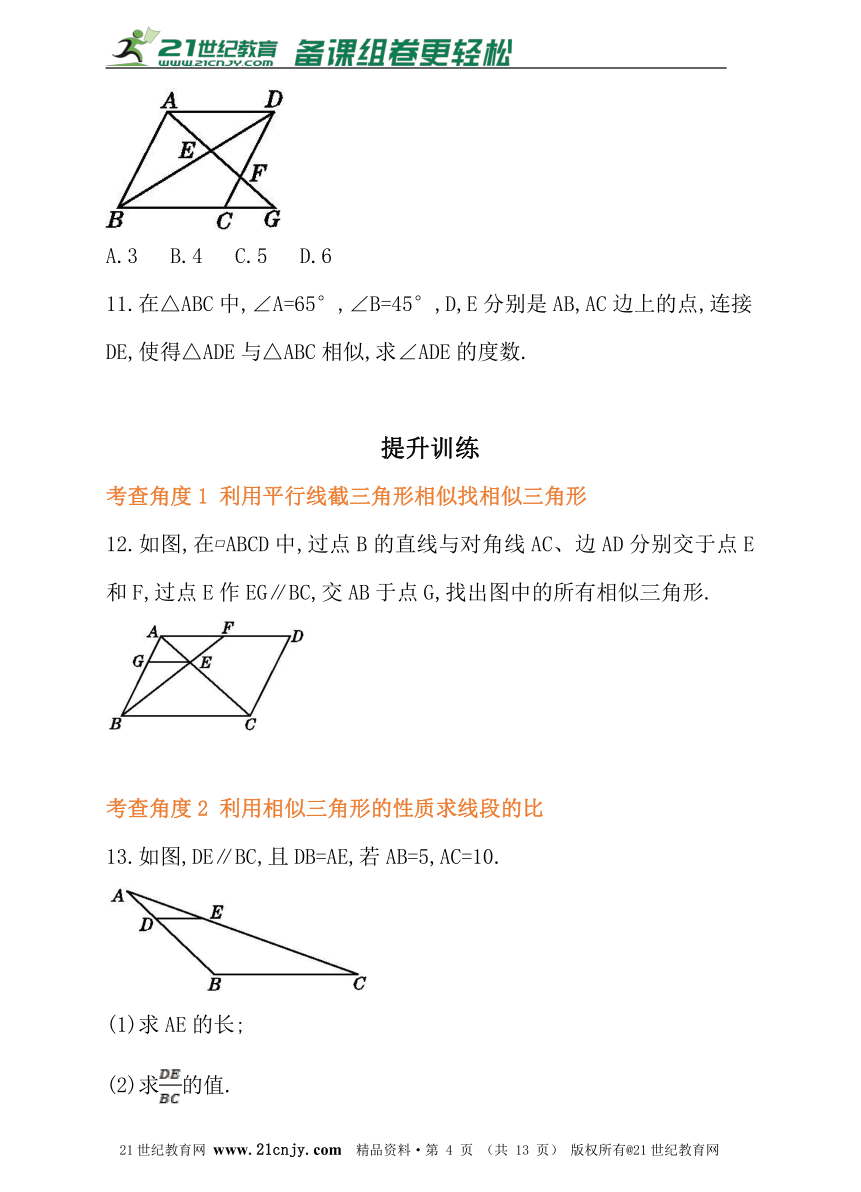
10.如图,在?ABCD中,G是BC延长线上一点,连接AG交BD于点E,交CD于点F.则图中相似三角形的对数为( )
A.3 B.4 C.5 D.6
11.在△ABC中,∠A=65°,∠B=45°,D,E分别是AB,AC边上的点,连接DE,使得△ADE与△ABC相似,求∠ADE的度数.
提升训练
考查角度1 利用平行线截三角形相似找相似三角形
12.如图,在?ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F,过点E作EG∥BC,交AB于点G,找出图中的所有相似三角形.
考查角度2 利用相似三角形的性质求线段的比
13.如图,DE∥BC,且DB=AE,若AB=5,AC=10.
(1)求AE的长;
(2)求的值.
14.如图,在?ABCD中,M,N为对角线BD的三等分点,连接AM并延长交BC于点E,连接EN并延长交AD于点F.21世纪教育网版权所有
(1)证明△AMD∽△EMB;
(2)求的值.
考查角度3 利用相似三角形的性质证比例式
15.如图,DE∥BC分别交AB,AC于D,E.
(1)写出图中的相似三角形;
(2)求证:=.
考查角度4 利用成比例线段证线段相等
16.如图,已知△ABC中,DE∥BC,BE与CD交于点O,连接AO并延长交BC于点M.
求证:BM=MC.
探究培优
拔尖角度1 利用相似三角形解与四边形综合应用问题(转化思想)
17.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.21·cn·jy·com
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP∶PB=1∶2,且PA⊥BF,求对角线BD的长.
拔尖角度2 利用比例线段证倍数关系(构造法)
18.如图,在△ABC中,点D为BC边的中点,延长AD至点E,延长AB交CE的延长线于点P.若AD=2DE,求证:AP=3AB.(至少用三种方法作辅助线)21教育网
拔尖角度3 利用平行线判定两三角形相似解与反比例函数的综合问题(数形结合思想)
19.如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标;
(3)结合(1)(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
参考答案
1.【答案】△AFD∽△EFC(或△EFC∽△EAB或△EAB∽△AFD)
2.【答案】△CDF,△ABP,△AED
3.【答案】C 4.【答案】C 5.【答案】C
6.【答案】 7.【答案】A 8.【答案】B
9.【答案】D
10.【答案】D
易错总结:本题容易出现错误的地方有两点:(1)忽略了三角形相似的传递性,因而漏掉了△AFD∽△GAB;(2)不理解三角形全等是三角形相似的特殊情况,因而漏掉了△ABD∽△CDB.21·世纪*教育网
11.错解:如图①,△ADE∽△ABC,则∠ADE=∠B=45°.
诊断:解决几何图形相似问题时,如果题中没有给出图形,那么往往要分情况讨论,此题错在考虑不周导致漏解.2-1-c-n-j-y
正解:如图①,当∠ADE对应∠B时,∠ADE=∠B=45°.如图②,当∠ADE对应∠C时,∠ADE=∠C=180°-(∠A+∠B)=70°.综上可知,∠ADE=45°或70°.【出处:21教育名师】
12.解:∵GE∥BC,∴△AGE∽△ABC.∵GE∥AF,∴△BGE∽△BAF.∵AF∥BC,∴△AEF∽△CEB;又∵△ABC≌△CDA,∴△ABC∽△CDA,△AGE∽△CDA.∴图中相似的三角形有5对.
13.解:(1)∵DE∥BC,
∴=.
设BD=AE=x,
则AD=AB-BD=5-x,
∴=.
∴x=,即AE=.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴==.
14.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BE.
∴△AMD∽△EMB.
(2)解:∵AD∥BC,
∴△FND∽△ENB.
∴=.
∵M,N为BD的三等分点,
∴=.
15.(1)解:△ADE∽△ABC,△OBC∽△OED.
(2)证明:∵△ADE∽△ABC,∴=.
∵△OBC∽△OED,∴=.∴=.
16.证明:延长AM,过点B作CD的平行线与AM的延长线交于点F,连接CF.
∵DE∥BC,BF∥CD,∴==.∴CF∥BE.
∴四边形OBFC为平行四边形.∴BM=MC.
17.(1)证明:∵四边形ABCD是菱形,
∴CD=AD,∠CDP=∠ADP,又∵DP=DP,
∴△CDP≌△ADP.∴∠DCP=∠DAP.
(2)解:∵四边形ABCD是菱形,∴CD∥BA,CD=BA.
∴△CDP∽△FBP,∴===,
∴CD=FB,CP=FP,∴A为BF的中点.
又∵PA⊥BF,∴PB=PF.
由(1)可知PA=CP,∴PA=PB.
在Rt△PAB中,PB2=AB2+PA2=22+,
解得PB=,∴PD=.∴BD=PD+PB=2.
方法总结:利用转化思想解关于相似三角形的综合题的方法:当图中存在相似三角形但利用相似三角形不能得到所需要的结果时,要看能否利用题目中的其他条件进行线段的转化或比的转化.通过转化很可能在已知与结论之间出现一座新的桥梁.www.21-cn-jy.com
18.思路导引:本题方法较多,可以过点B(或C,D,A)添加平行线,来构造相似三角形,通过对应线段成比例来得出结论.2·1·c·n·j·y
证明:过点B作BF∥AE交PC于点F,如图①.
∵BF∥DE,点D为BC的中点,
∴DE为△BFC的中位线,∴BF=2DE.
∵AD=2DE,∴AD=AE,∴BF=AD=AE.
∵BF∥AE,∴△PBF∽△PAE,
∴==,∴PB=PA.∴AP=3AB.
方法总结:此题的证明方法很多,我们可以结合下面提供的辅助线,找出证明方法.
方法二:作BG∥PC交AE于点G,如图②;
方法三:作DH∥AB交PC于点H,如图③;
方法四:作DQ∥PC交AP于点Q,如图④;
方法五:作CS∥AB交AE的延长线于点S,如图⑤;
方法六:作CT∥AD交BA的延长线于点T,如图⑥;
方法七:作AK∥PC交CB的延长线于点K,如图⑦;
方法八:作AL∥BC交PC的延长线于点L,如图⑧.
19.解:(1)把A(1,3)代入y=,得k=3,把B(3,y2)代入y=,得y2=1,∴B(3,1).【来源:21·世纪·教育·网】
把A(1,3),B(3,1)分别代入y=ax+b,得解得
∴yAB=-x+4.令yAB=0,得x=4,∴P(4,0).
(2)∵AB=PB,∴B是AP的中点,由中点坐标公式知:x2=,y2=,
∵A,B两点都在双曲线上,∴x1y1=·,解得x1=2,∴x2=4.
作AD⊥x轴于点D,则△PAD∽△PCO,
∴=,即=,又b=y1+1,
∴y1=2,∴y2=1.
∴A(2,2),B(4,1).
(3)x1+x2=x0.
点拨:(3)∵A(x1,y1),B(x2,y2),∴
解得∴y=x-.
令y=0,得x=,∵x1y1=x2y2,∴x===x1+x2,即x1+x2=x0.
基础训练
知识点1 平行线截三角形相似定理
1.如图,E为平行四边形ABCD的边BC延长线上一点,连接AE,交边CD于点F.在不添加辅助线的情况下,请写出图中一对相似三角形: .?21cnjy.com
2.如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出所有与△BEF相似的三角形: .www-2-1-cnjy-com
3.如图,在△ABC中,EF∥BC,DG∥AB,EF和DG相交于点H,则图中与△ABC相似的三角形共有( )21*cnjy*com
A.1个 B.2个 C.3个 D.4个
4.如图,AB∥CD,AE∥FD,AE,FD分别交BC于点G,H,则图中共有相似三角形( )
A.4对 B.5对 C.6对 D.7对
5.如图,G是平行四边形ABCD的边CD延长线上一点,BG交AC于E,交AD于F,则图中与△FGD相似的三角形有( )【来源:21cnj*y.co*m】
A.0个 B.1个 C.2个 D.3个
知识点2 平行线截三角形相似定理的应用
6.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,则= .【版权所有:21教育】
7.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且
DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A. B. C. D.
8.如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若AD=1,BC=3,则的值为( )21教育名师原创作品
A. B. C. D.
9.如图,在?ABCD中,点E是边AD上一点,EC交对角线BD于点F,若EF∶FC=4∶7,则AE∶ED等于( )21*cnjy*com
A.4∶7 B.4∶3 C.3∶7 D.3∶4
10.如图,在?ABCD中,G是BC延长线上一点,连接AG交BD于点E,交CD于点F.则图中相似三角形的对数为( )
A.3 B.4 C.5 D.6
11.在△ABC中,∠A=65°,∠B=45°,D,E分别是AB,AC边上的点,连接DE,使得△ADE与△ABC相似,求∠ADE的度数.
提升训练
考查角度1 利用平行线截三角形相似找相似三角形
12.如图,在?ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F,过点E作EG∥BC,交AB于点G,找出图中的所有相似三角形.
考查角度2 利用相似三角形的性质求线段的比
13.如图,DE∥BC,且DB=AE,若AB=5,AC=10.
(1)求AE的长;
(2)求的值.
14.如图,在?ABCD中,M,N为对角线BD的三等分点,连接AM并延长交BC于点E,连接EN并延长交AD于点F.21世纪教育网版权所有
(1)证明△AMD∽△EMB;
(2)求的值.
考查角度3 利用相似三角形的性质证比例式
15.如图,DE∥BC分别交AB,AC于D,E.
(1)写出图中的相似三角形;
(2)求证:=.
考查角度4 利用成比例线段证线段相等
16.如图,已知△ABC中,DE∥BC,BE与CD交于点O,连接AO并延长交BC于点M.
求证:BM=MC.
探究培优
拔尖角度1 利用相似三角形解与四边形综合应用问题(转化思想)
17.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.21·cn·jy·com
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP∶PB=1∶2,且PA⊥BF,求对角线BD的长.
拔尖角度2 利用比例线段证倍数关系(构造法)
18.如图,在△ABC中,点D为BC边的中点,延长AD至点E,延长AB交CE的延长线于点P.若AD=2DE,求证:AP=3AB.(至少用三种方法作辅助线)21教育网
拔尖角度3 利用平行线判定两三角形相似解与反比例函数的综合问题(数形结合思想)
19.如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标;
(3)结合(1)(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
参考答案
1.【答案】△AFD∽△EFC(或△EFC∽△EAB或△EAB∽△AFD)
2.【答案】△CDF,△ABP,△AED
3.【答案】C 4.【答案】C 5.【答案】C
6.【答案】 7.【答案】A 8.【答案】B
9.【答案】D
10.【答案】D
易错总结:本题容易出现错误的地方有两点:(1)忽略了三角形相似的传递性,因而漏掉了△AFD∽△GAB;(2)不理解三角形全等是三角形相似的特殊情况,因而漏掉了△ABD∽△CDB.21·世纪*教育网
11.错解:如图①,△ADE∽△ABC,则∠ADE=∠B=45°.
诊断:解决几何图形相似问题时,如果题中没有给出图形,那么往往要分情况讨论,此题错在考虑不周导致漏解.2-1-c-n-j-y
正解:如图①,当∠ADE对应∠B时,∠ADE=∠B=45°.如图②,当∠ADE对应∠C时,∠ADE=∠C=180°-(∠A+∠B)=70°.综上可知,∠ADE=45°或70°.【出处:21教育名师】
12.解:∵GE∥BC,∴△AGE∽△ABC.∵GE∥AF,∴△BGE∽△BAF.∵AF∥BC,∴△AEF∽△CEB;又∵△ABC≌△CDA,∴△ABC∽△CDA,△AGE∽△CDA.∴图中相似的三角形有5对.
13.解:(1)∵DE∥BC,
∴=.
设BD=AE=x,
则AD=AB-BD=5-x,
∴=.
∴x=,即AE=.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴==.
14.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BE.
∴△AMD∽△EMB.
(2)解:∵AD∥BC,
∴△FND∽△ENB.
∴=.
∵M,N为BD的三等分点,
∴=.
15.(1)解:△ADE∽△ABC,△OBC∽△OED.
(2)证明:∵△ADE∽△ABC,∴=.
∵△OBC∽△OED,∴=.∴=.
16.证明:延长AM,过点B作CD的平行线与AM的延长线交于点F,连接CF.
∵DE∥BC,BF∥CD,∴==.∴CF∥BE.
∴四边形OBFC为平行四边形.∴BM=MC.
17.(1)证明:∵四边形ABCD是菱形,
∴CD=AD,∠CDP=∠ADP,又∵DP=DP,
∴△CDP≌△ADP.∴∠DCP=∠DAP.
(2)解:∵四边形ABCD是菱形,∴CD∥BA,CD=BA.
∴△CDP∽△FBP,∴===,
∴CD=FB,CP=FP,∴A为BF的中点.
又∵PA⊥BF,∴PB=PF.
由(1)可知PA=CP,∴PA=PB.
在Rt△PAB中,PB2=AB2+PA2=22+,
解得PB=,∴PD=.∴BD=PD+PB=2.
方法总结:利用转化思想解关于相似三角形的综合题的方法:当图中存在相似三角形但利用相似三角形不能得到所需要的结果时,要看能否利用题目中的其他条件进行线段的转化或比的转化.通过转化很可能在已知与结论之间出现一座新的桥梁.www.21-cn-jy.com
18.思路导引:本题方法较多,可以过点B(或C,D,A)添加平行线,来构造相似三角形,通过对应线段成比例来得出结论.2·1·c·n·j·y
证明:过点B作BF∥AE交PC于点F,如图①.
∵BF∥DE,点D为BC的中点,
∴DE为△BFC的中位线,∴BF=2DE.
∵AD=2DE,∴AD=AE,∴BF=AD=AE.
∵BF∥AE,∴△PBF∽△PAE,
∴==,∴PB=PA.∴AP=3AB.
方法总结:此题的证明方法很多,我们可以结合下面提供的辅助线,找出证明方法.
方法二:作BG∥PC交AE于点G,如图②;
方法三:作DH∥AB交PC于点H,如图③;
方法四:作DQ∥PC交AP于点Q,如图④;
方法五:作CS∥AB交AE的延长线于点S,如图⑤;
方法六:作CT∥AD交BA的延长线于点T,如图⑥;
方法七:作AK∥PC交CB的延长线于点K,如图⑦;
方法八:作AL∥BC交PC的延长线于点L,如图⑧.
19.解:(1)把A(1,3)代入y=,得k=3,把B(3,y2)代入y=,得y2=1,∴B(3,1).【来源:21·世纪·教育·网】
把A(1,3),B(3,1)分别代入y=ax+b,得解得
∴yAB=-x+4.令yAB=0,得x=4,∴P(4,0).
(2)∵AB=PB,∴B是AP的中点,由中点坐标公式知:x2=,y2=,
∵A,B两点都在双曲线上,∴x1y1=·,解得x1=2,∴x2=4.
作AD⊥x轴于点D,则△PAD∽△PCO,
∴=,即=,又b=y1+1,
∴y1=2,∴y2=1.
∴A(2,2),B(4,1).
(3)x1+x2=x0.
点拨:(3)∵A(x1,y1),B(x2,y2),∴
解得∴y=x-.
令y=0,得x=,∵x1y1=x2y2,∴x===x1+x2,即x1+x2=x0.
