27.2.1 利用两边及夹角判定三角形相似定理 同步练习
文档属性
| 名称 | 27.2.1 利用两边及夹角判定三角形相似定理 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 526.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览

文档简介
27.2.4利用两边及夹角判定三角形相似定理
基础训练
知识点 两边及夹角判定相似三角形定理
1.能判定△ABC和△A'B'C'相似的条件是( )
A.=,且∠B=∠B'
B.=,且∠A=∠C'
C.=,且∠B=∠A'
D.=,且∠A=∠B'
2.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )21世纪教育网版权所有
A.P1 B.P2 C.P3 D.P4
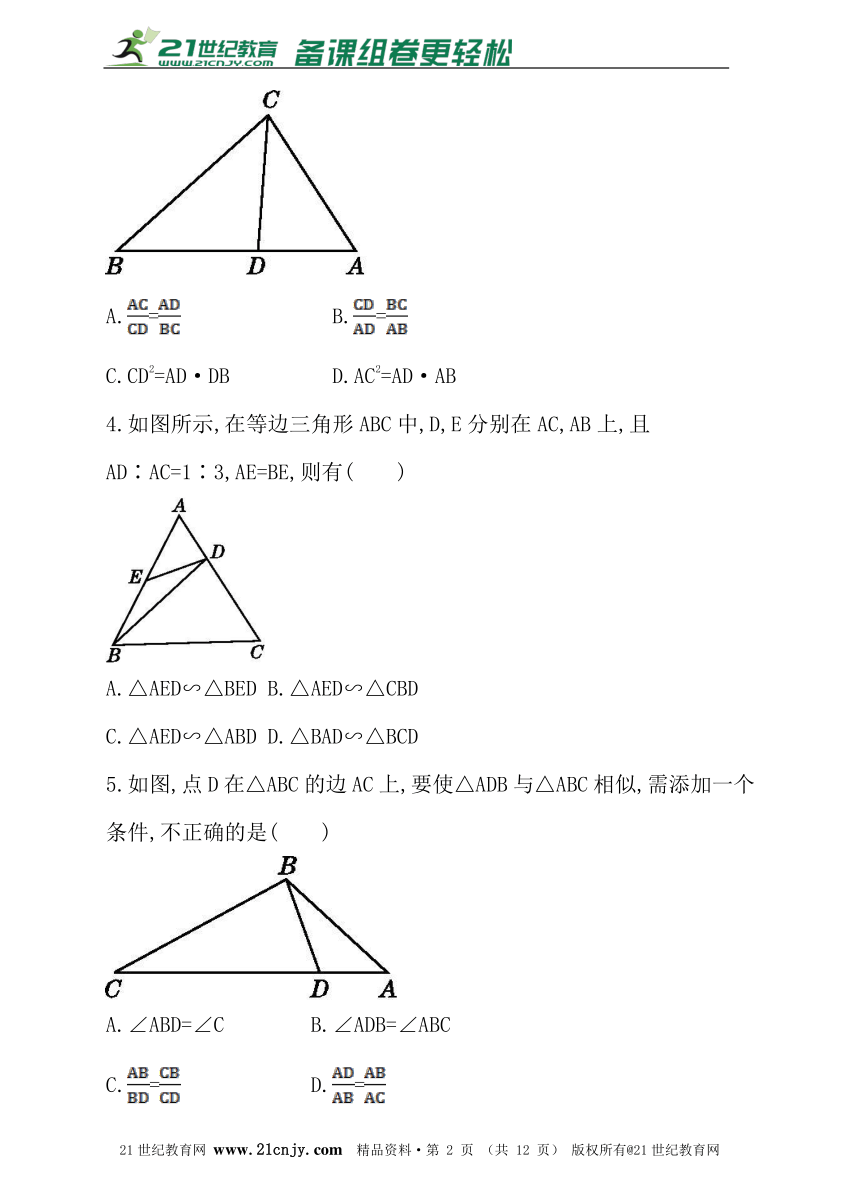
3.如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
4.如图所示,在等边三角形ABC中,D,E分别在AC,AB上,且
AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
5.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,需添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC
C.= D.=
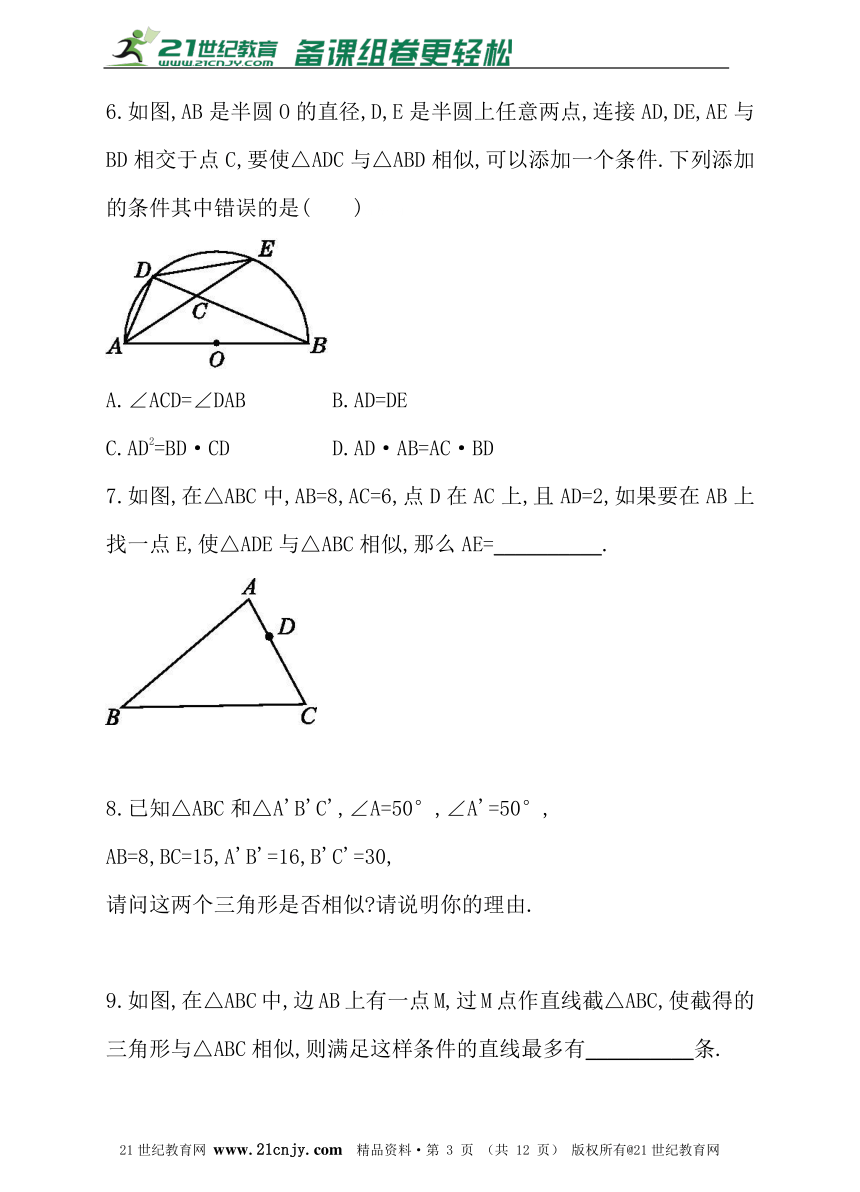
6.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )21教育网
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.AD·AB=AC·BD
7.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,那么AE=__________.
8.已知△ABC和△A'B'C',∠A=50°,∠A'=50°,
AB=8,BC=15,A'B'=16,B'C'=30,
请问这两个三角形是否相似?请说明你的理由.
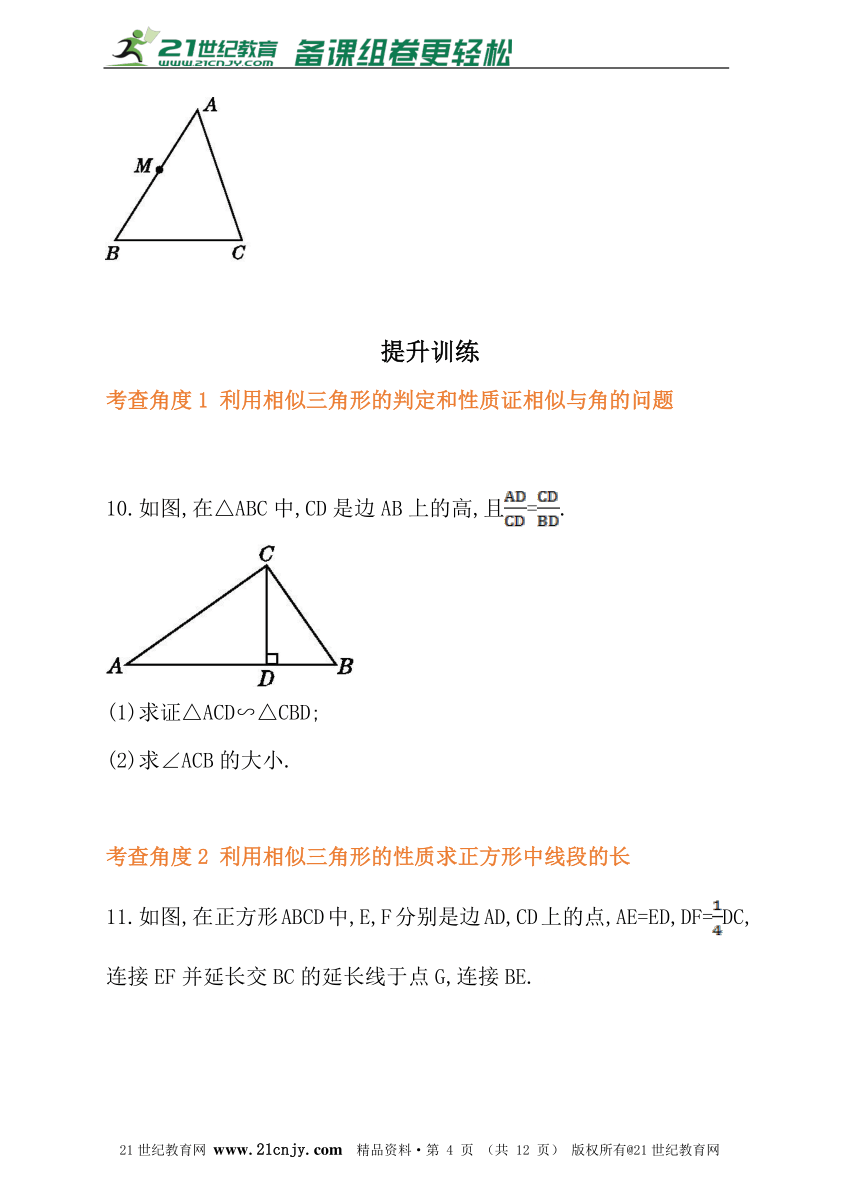
9.如图,在△ABC中,边AB上有一点M,过M点作直线截△ABC,使截得的三角形与△ABC相似,则满足这样条件的直线最多有__________条.
?
提升训练
考查角度1 利用相似三角形的判定和性质证相似与角的问题
10.如图,在△ABC中,CD是边AB上的高,且=.
(1)求证△ACD∽△CBD;
(2)求∠ACB的大小.
考查角度2 利用相似三角形的性质求正方形中线段的长
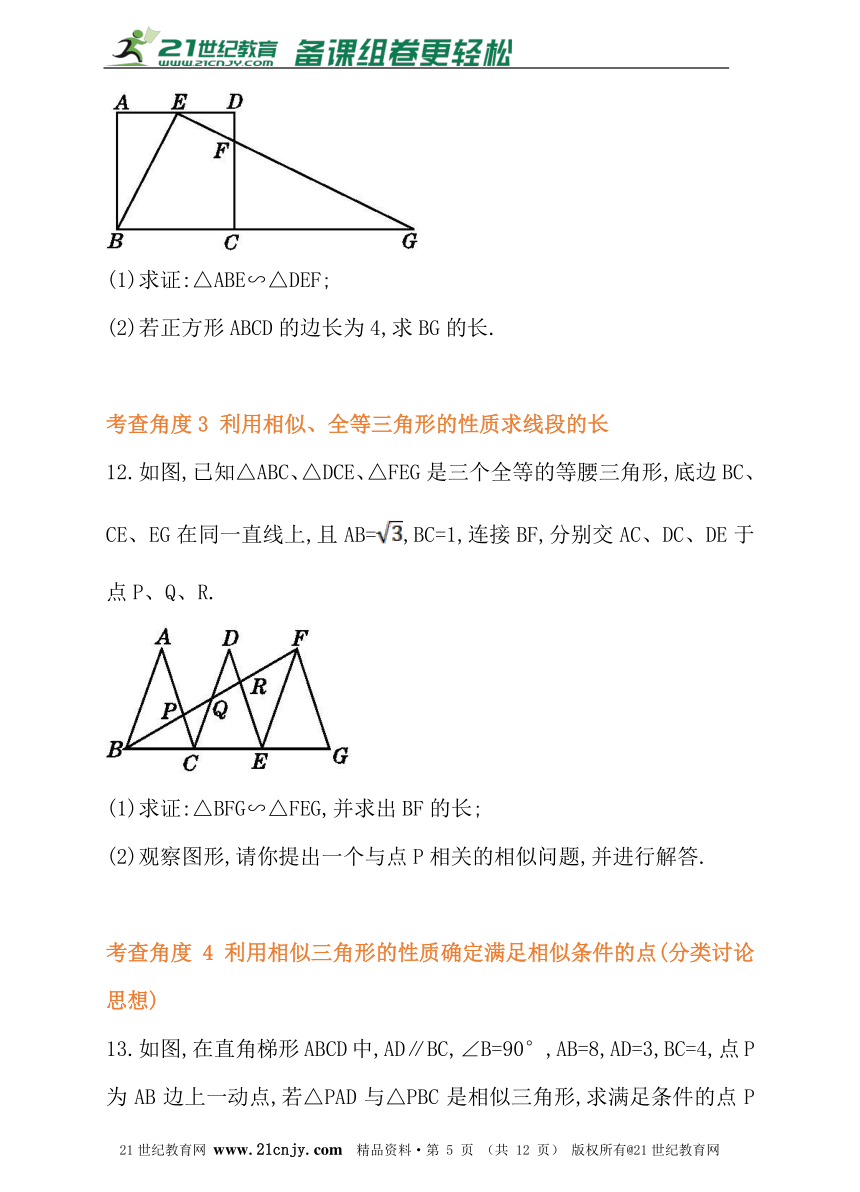
11.如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G,连接BE.21cnjy.com
(1)求证:△ABE∽△DEF;
(2)若正方形ABCD的边长为4,求BG的长.
考查角度3 利用相似、全等三角形的性质求线段的长
12.如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.21·cn·jy·com
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的相似问题,并进行解答.
考查角度4 利用相似三角形的性质确定满足相似条件的点(分类讨论思想)
13.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求满足条件的点P的个数;并求出相应的AP的长.www.21-cn-jy.com
14.如图①,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.2·1·c·n·j·y
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图②,若AD,BC所在直线互相垂直,求的值.
① ②
15.如图,已知AB是☉O的直径,BC是☉O的弦,弦ED⊥AB于点F,交BC于点G,过点C的直线与ED的延长线交于点P,PC=PG.
(1)求证:PC是☉O的切线;
(2)当点C在劣弧AD上运动时,其他条件不变,若BG2=BF·BO,求证:点G是BC的中点;
(3)在满足(2)的条件下,若AB=10,ED=4.求BG的长.
参考答案
1.【答案】C 2.【答案】C 3.【答案】D
4.【答案】B 5.【答案】C 6.【答案】D
7.【答案】或
8.解:△ABC与△A'B'C'不一定相似.理由如下:因为∠A=∠A'=50°,但不知道是否等于,所以根据已知条件不能确定△ABC与△A'B'C'相似.【来源:21·世纪·教育·网】
易错总结:根据边角对应关系判断两个三角形相似,应具备“两边对应成比例,且夹角相等”,本题中虽然==,但BC,B'C'分别是∠A,∠A'的对边,不满足“两边成比例且夹角相等”,不能由此来判断△ABC与△A'B'C'相似.21·世纪*教育网
9.【答案】4
解:(1)过M作BC的平行线.
(2)过M作AC的平行线.(3)在AC上取点N使=.
(4)在BC上取点P使=.
10.(1)证明:∵CD⊥AB,∴∠ADC=∠CDB=90°.
又∵=,
∴△ACD∽△CBD.
(2)解:∵△ACD∽△CBD,
∴∠A=∠BCD.
又∵∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
11.(1)证明:在正方形ABCD中,∠A=∠D=90°,AB=AD=CD.
∵AE=ED,DF=DC,
∴AE=ED=AB,DF=AB,
∴=,∴△ABE∽△DEF.
(2)解:∵AD=4,AE=ED,∴DE=2.∵AD∥CG,
∴△EFD∽△GFC,∴==,
∴CG=3DE=6,∴BG=10.
12.(1)证明:∵△ABC≌△DCE≌△FEG,∴FG=AB=,BC=CE=EG=BG=1,即BG=3.∴===,又∠BGF=∠FGE,∴△BFG∽△FEG.∵△FEG是等腰三角形,∴△BFG是等腰三角形,∴BF=BG=3.www-2-1-cnjy-com
(2)解:本题答案不唯一,如求证:△APB∽△CPQ.证明如下:∵△ABC≌△DCE,∴∠ABC=∠DCE,∴AB∥CD,2-1-c-n-j-y
∴△APB∽△CPQ.
13.解:∵AD∥BC,∠B=90°,∴∠A=180°-∠B=90°,
∴∠PAD=∠PBC=90°.
设AP的长为x,则BP=AB-AP=8-x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP∶BP=AD∶BC,即x∶(8-x)=3∶4,解得x=;②若△APD∽△BCP,则AP∶BC=AD∶BP,即x∶4=3∶(8-x),解得x=2或x=6.21*cnjy*com
∴满足条件的点P的个数是3.
14.(1)证明:∵点E,F分别为AB,CD的中点,且GF⊥CD,GE⊥AB,
∴GA=GB,GD=GC.
在△AGD与△BGC中,
∴△AGD≌△BGC.
∴AD=BC.
(2)证明:由(1)得∠AGD=∠EGF.∵∠AGD=∠EGF,
∴∠AGB=∠DGC.
又∵=,
∴△AGB∽△DGC.
又∵GE,GF分别为等腰三角形△AGB和△DGC底边AB,DC上的高,
∴=且∠AGE=∠AGB=∠DGC=∠DGF.
∴=,且∠AGD=∠EGF.
∴△AGD∽△ECF.
(3)解:延长AD,BC交于点O,AO,GB交于点P.
∵△AGD≌△BGC,
∴∠GAD=∠GBC.
又∵∠OPB=∠GPA,
∴∠AGP=∠POB=90°.
又∵GA=GB,
∴∠GAE=∠AGE=45°.
∴==.
15.(1)证明:如图,连接OC.∵ED⊥AB,∴∠BFG=90°,∴∠B+∠BGF=90°.
∵PC=PG,∴∠PCG=∠PGC,
而∠PGC=∠BGF.
∴∠B+∠PCG=90°.
∵OB=OC,∴∠B=∠BCO.
∴∠BCO+∠PCG=90°,
则∠PCO=90°,即OC⊥PC,
而OC是半径,∴PC是☉O的切线.
(2)证明:如图,连接OG.
∵BG2=BF·BO,∴=,
而∠B=∠B,∴△BFG∽△BGO,∴∠BGO=∠BFG=90°.
∴OG⊥BC,∴点G是BC的中点.
(3)解:如图,连接OE.
∵AB是☉O的直径,ED⊥AB,∴EF=ED.
∵AB=10,ED=4,
∴EF=2,OE=OB=AB=5.
在Rt△OEF中,OF==1,
∴BF=OB-OF=5-1=4.
∴BG==2.
基础训练
知识点 两边及夹角判定相似三角形定理
1.能判定△ABC和△A'B'C'相似的条件是( )
A.=,且∠B=∠B'
B.=,且∠A=∠C'
C.=,且∠B=∠A'
D.=,且∠A=∠B'
2.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )21世纪教育网版权所有
A.P1 B.P2 C.P3 D.P4
3.如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
4.如图所示,在等边三角形ABC中,D,E分别在AC,AB上,且
AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
5.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,需添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC
C.= D.=
6.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )21教育网
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.AD·AB=AC·BD
7.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,那么AE=__________.
8.已知△ABC和△A'B'C',∠A=50°,∠A'=50°,
AB=8,BC=15,A'B'=16,B'C'=30,
请问这两个三角形是否相似?请说明你的理由.
9.如图,在△ABC中,边AB上有一点M,过M点作直线截△ABC,使截得的三角形与△ABC相似,则满足这样条件的直线最多有__________条.
?
提升训练
考查角度1 利用相似三角形的判定和性质证相似与角的问题
10.如图,在△ABC中,CD是边AB上的高,且=.
(1)求证△ACD∽△CBD;
(2)求∠ACB的大小.
考查角度2 利用相似三角形的性质求正方形中线段的长
11.如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=DC,连接EF并延长交BC的延长线于点G,连接BE.21cnjy.com
(1)求证:△ABE∽△DEF;
(2)若正方形ABCD的边长为4,求BG的长.
考查角度3 利用相似、全等三角形的性质求线段的长
12.如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.21·cn·jy·com
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的相似问题,并进行解答.
考查角度4 利用相似三角形的性质确定满足相似条件的点(分类讨论思想)
13.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求满足条件的点P的个数;并求出相应的AP的长.www.21-cn-jy.com
14.如图①,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.2·1·c·n·j·y
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图②,若AD,BC所在直线互相垂直,求的值.
① ②
15.如图,已知AB是☉O的直径,BC是☉O的弦,弦ED⊥AB于点F,交BC于点G,过点C的直线与ED的延长线交于点P,PC=PG.
(1)求证:PC是☉O的切线;
(2)当点C在劣弧AD上运动时,其他条件不变,若BG2=BF·BO,求证:点G是BC的中点;
(3)在满足(2)的条件下,若AB=10,ED=4.求BG的长.
参考答案
1.【答案】C 2.【答案】C 3.【答案】D
4.【答案】B 5.【答案】C 6.【答案】D
7.【答案】或
8.解:△ABC与△A'B'C'不一定相似.理由如下:因为∠A=∠A'=50°,但不知道是否等于,所以根据已知条件不能确定△ABC与△A'B'C'相似.【来源:21·世纪·教育·网】
易错总结:根据边角对应关系判断两个三角形相似,应具备“两边对应成比例,且夹角相等”,本题中虽然==,但BC,B'C'分别是∠A,∠A'的对边,不满足“两边成比例且夹角相等”,不能由此来判断△ABC与△A'B'C'相似.21·世纪*教育网
9.【答案】4
解:(1)过M作BC的平行线.
(2)过M作AC的平行线.(3)在AC上取点N使=.
(4)在BC上取点P使=.
10.(1)证明:∵CD⊥AB,∴∠ADC=∠CDB=90°.
又∵=,
∴△ACD∽△CBD.
(2)解:∵△ACD∽△CBD,
∴∠A=∠BCD.
又∵∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
11.(1)证明:在正方形ABCD中,∠A=∠D=90°,AB=AD=CD.
∵AE=ED,DF=DC,
∴AE=ED=AB,DF=AB,
∴=,∴△ABE∽△DEF.
(2)解:∵AD=4,AE=ED,∴DE=2.∵AD∥CG,
∴△EFD∽△GFC,∴==,
∴CG=3DE=6,∴BG=10.
12.(1)证明:∵△ABC≌△DCE≌△FEG,∴FG=AB=,BC=CE=EG=BG=1,即BG=3.∴===,又∠BGF=∠FGE,∴△BFG∽△FEG.∵△FEG是等腰三角形,∴△BFG是等腰三角形,∴BF=BG=3.www-2-1-cnjy-com
(2)解:本题答案不唯一,如求证:△APB∽△CPQ.证明如下:∵△ABC≌△DCE,∴∠ABC=∠DCE,∴AB∥CD,2-1-c-n-j-y
∴△APB∽△CPQ.
13.解:∵AD∥BC,∠B=90°,∴∠A=180°-∠B=90°,
∴∠PAD=∠PBC=90°.
设AP的长为x,则BP=AB-AP=8-x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP∶BP=AD∶BC,即x∶(8-x)=3∶4,解得x=;②若△APD∽△BCP,则AP∶BC=AD∶BP,即x∶4=3∶(8-x),解得x=2或x=6.21*cnjy*com
∴满足条件的点P的个数是3.
14.(1)证明:∵点E,F分别为AB,CD的中点,且GF⊥CD,GE⊥AB,
∴GA=GB,GD=GC.
在△AGD与△BGC中,
∴△AGD≌△BGC.
∴AD=BC.
(2)证明:由(1)得∠AGD=∠EGF.∵∠AGD=∠EGF,
∴∠AGB=∠DGC.
又∵=,
∴△AGB∽△DGC.
又∵GE,GF分别为等腰三角形△AGB和△DGC底边AB,DC上的高,
∴=且∠AGE=∠AGB=∠DGC=∠DGF.
∴=,且∠AGD=∠EGF.
∴△AGD∽△ECF.
(3)解:延长AD,BC交于点O,AO,GB交于点P.
∵△AGD≌△BGC,
∴∠GAD=∠GBC.
又∵∠OPB=∠GPA,
∴∠AGP=∠POB=90°.
又∵GA=GB,
∴∠GAE=∠AGE=45°.
∴==.
15.(1)证明:如图,连接OC.∵ED⊥AB,∴∠BFG=90°,∴∠B+∠BGF=90°.
∵PC=PG,∴∠PCG=∠PGC,
而∠PGC=∠BGF.
∴∠B+∠PCG=90°.
∵OB=OC,∴∠B=∠BCO.
∴∠BCO+∠PCG=90°,
则∠PCO=90°,即OC⊥PC,
而OC是半径,∴PC是☉O的切线.
(2)证明:如图,连接OG.
∵BG2=BF·BO,∴=,
而∠B=∠B,∴△BFG∽△BGO,∴∠BGO=∠BFG=90°.
∴OG⊥BC,∴点G是BC的中点.
(3)解:如图,连接OE.
∵AB是☉O的直径,ED⊥AB,∴EF=ED.
∵AB=10,ED=4,
∴EF=2,OE=OB=AB=5.
在Rt△OEF中,OF==1,
∴BF=OB-OF=5-1=4.
∴BG==2.
