27.2.1 利用两角及直角三角形判定三角形相似定理 同步练习
文档属性
| 名称 | 27.2.1 利用两角及直角三角形判定三角形相似定理 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 583.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 22:30:39 | ||
图片预览

文档简介
27.2.5利用两角及直角三角形判定三角形相似定理
基础训练
知识点1 用两组角判定两三角形相似
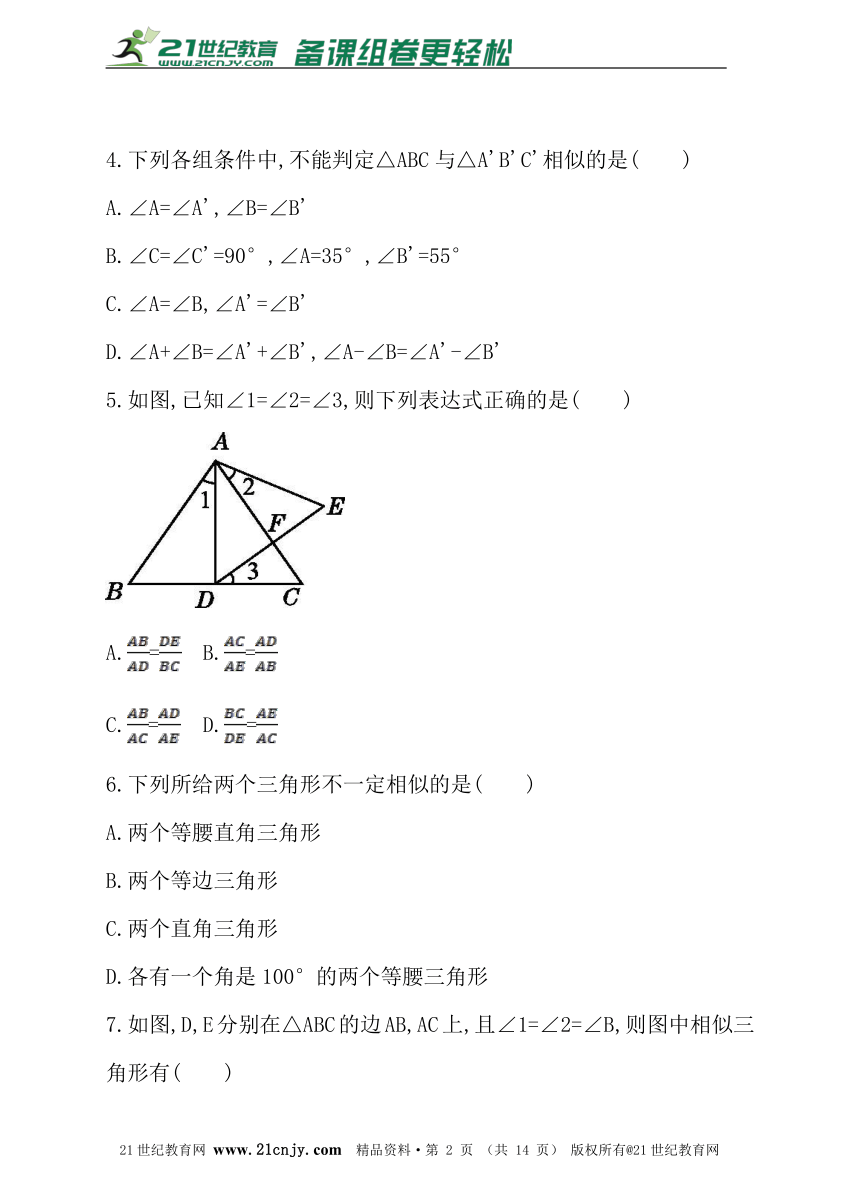
1.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中的相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,则下列三角形中,与△BOC一定相似的是( )21·世纪*教育网
A.△ABD B.△DOA C.△ACD D.△ABO
3.如图,在△ABC中,BD,CE是高,则与△BOE相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
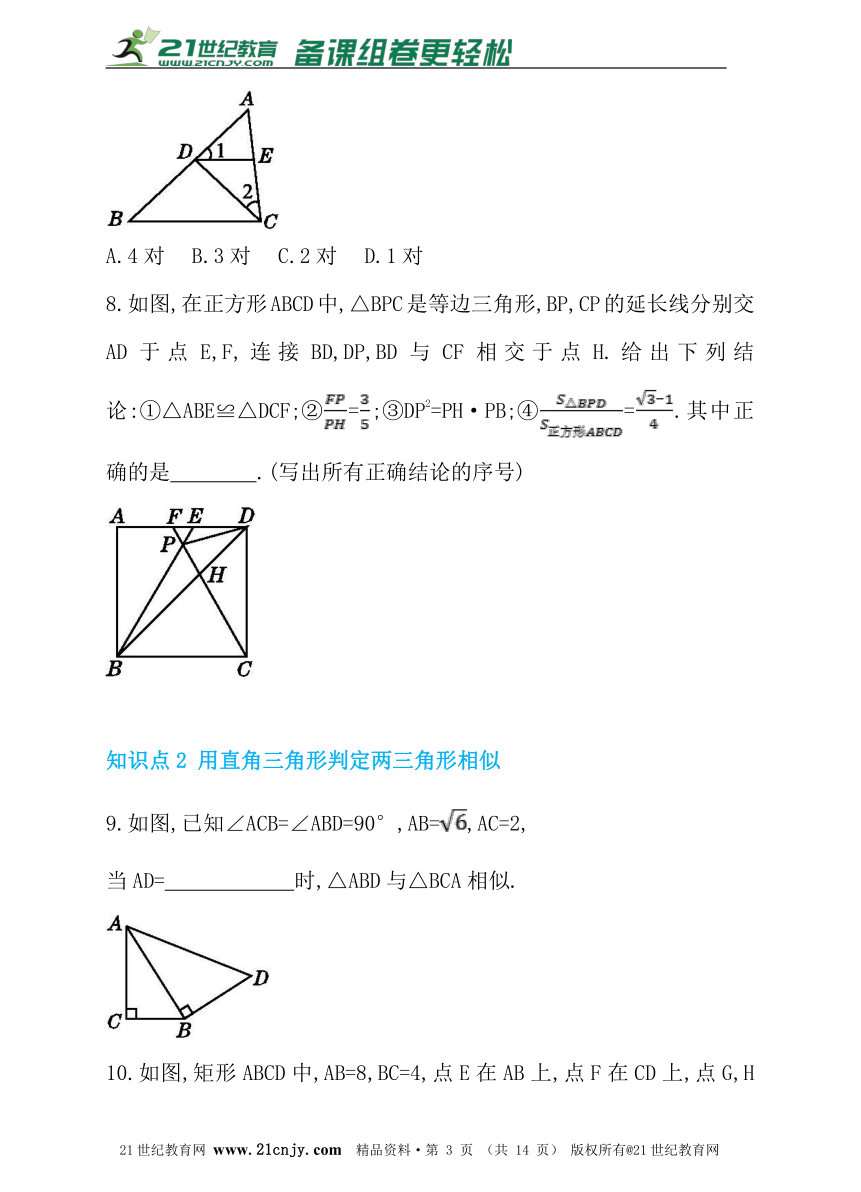
4.下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A.∠A=∠A',∠B=∠B'
B.∠C=∠C'=90°,∠A=35°,∠B'=55°
C.∠A=∠B,∠A'=∠B'
D.∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
5.如图,已知∠1=∠2=∠3,则下列表达式正确的是( )
A.= B.=
C.= D.=
6.下列所给两个三角形不一定相似的是( )
A.两个等腰直角三角形
B.两个等边三角形
C.两个直角三角形
D.各有一个角是100°的两个等腰三角形
7.如图,D,E分别在△ABC的边AB,AC上,且∠1=∠2=∠B,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
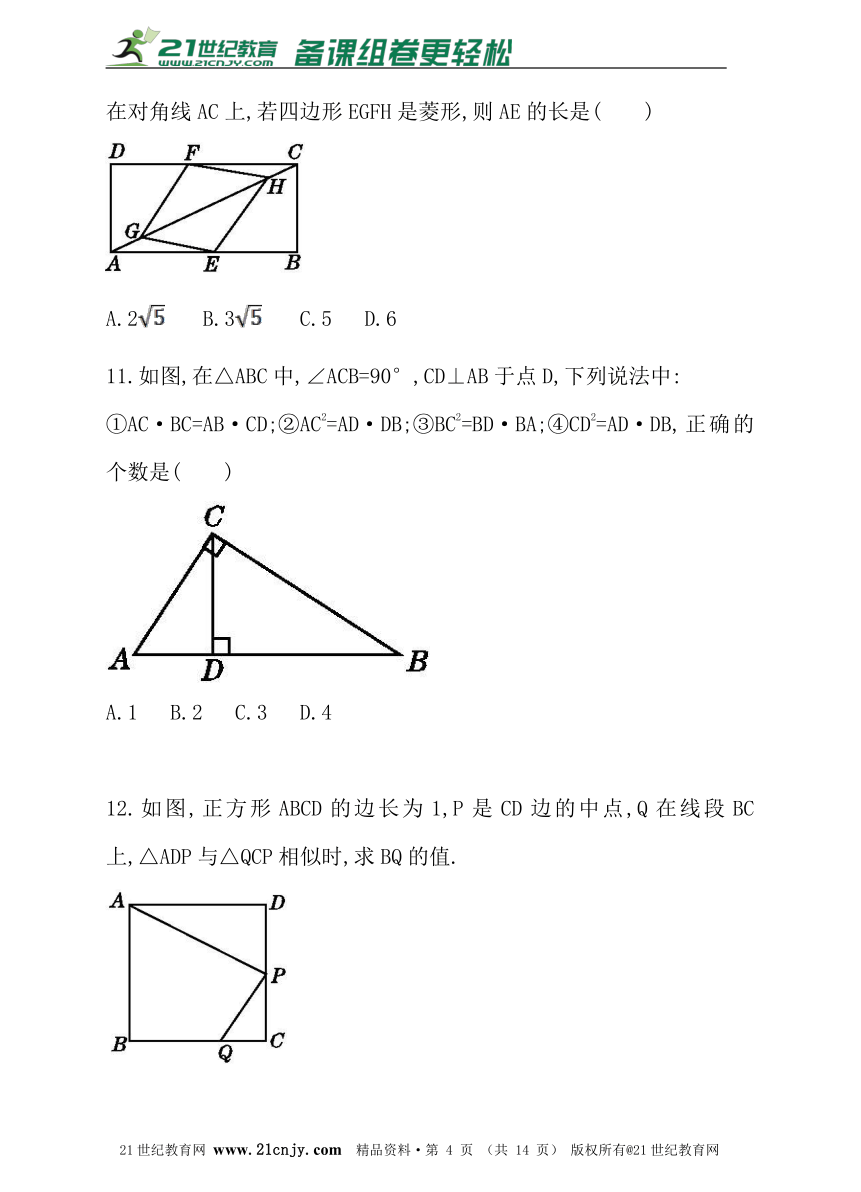
8.如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②=;③DP2=PH·PB;④=.其中正确的是 .(写出所有正确结论的序号)21cnjy.com
知识点2 用直角三角形判定两三角形相似
9.如图,已知∠ACB=∠ABD=90°,AB=,AC=2,
当AD= 时,△ABD与△BCA相似.?
10.如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
11.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列说法中:
①AC·BC=AB·CD;②AC2=AD·DB;③BC2=BD·BA;④CD2=AD·DB,正确的个数是( )www.21-cn-jy.com
A.1 B.2 C.3 D.4
12.如图,正方形ABCD的边长为1,P是CD边的中点,Q在线段BC上,△ADP与△QCP相似时,求BQ的值.www-2-1-cnjy-com
提升训练
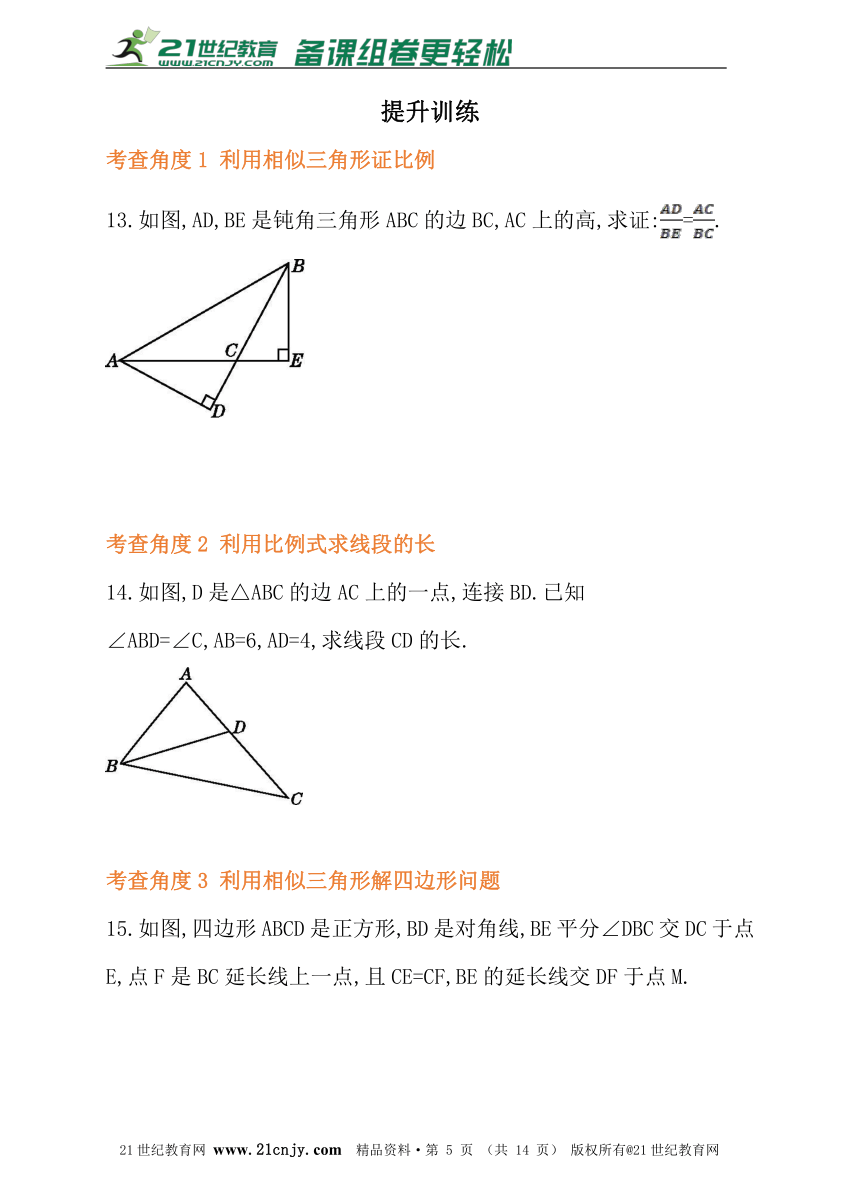
考查角度1 利用相似三角形证比例
13.如图,AD,BE是钝角三角形ABC的边BC,AC上的高,求证:=.
考查角度2 利用比例式求线段的长
14.如图,D是△ABC的边AC上的一点,连接BD.已知
∠ABD=∠C,AB=6,AD=4,求线段CD的长.
考查角度3 利用相似三角形解四边形问题
15.如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于点E,点F是BC延长线上一点,且CE=CF,BE的延长线交DF于点M.
(1)求证:BM⊥DF;
(2)若正方形ABCD的边长为2,求ME·MB.
考查角度4 利用相似三角形解与全等相关的问题
16.如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.
求证:(1)△ACE≌△BCD;
(2)=.
17.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC,AB于点E,F.21世纪教育网版权所有
(1)若∠B=30°,求证:以A,O,D,E为顶点的四边形是菱形;
(2)若AC=6,AB=10,连接AD,求☉O的半径和AD的长.
18.如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动,当两个动点运动了x秒(0(1)求点N的坐标(用含x的代数式表示).
(2)设△OMN的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.21教育网
参考答案
1.【答案】C 2.【答案】B 3.【答案】C
4.【答案】C 5.【答案】C 6.【答案】C
7.【答案】A 8.【答案】①③④
9.【答案】3或3
10.【答案】C
解:连接EF.若四边形EGFH为菱形,则EF⊥GH,假设线段EF,GH交于点O,则O为AC中点,故AO=AC=2,又△ABC∽△AOE,则==,解得AE=5,故选C.21·cn·jy·com
11.【答案】C
12.解:由题意,得∠D=∠C=90°.
①当△ADP∽△PCQ时,=,
即=,得CQ=.
故BQ=1-=.
②当△ADP∽△QCP时,=,
即=,得QC=1,故BQ=0.
所以当△ADP与△QCP相似时,BQ的值为0或.
跳出误区:因为题中∠D=∠C=90°,所以直角三角形相似在对应顺序上有两种可能,即△ADP∽△PCQ或△ADP∽△QCP,此题容易因只考虑一种情况而漏解.2·1·c·n·j·y
13.证明:在△ACD和△BCE中,∵∠D=∠E=90°,∠ACD=∠BCE,∴△ACD∽△BCE,∴=.【来源:21·世纪·教育·网】
14.解:∵∠A=∠A,∠ABD=∠C,
∴△ABD∽△ACB,∴=,∴AB2=AD·AC.
又AB=6,AD=4,∴AC=9,∴CD=AC-AD=5.
15.(1)证明:∵四边形ABCD是正方形,∴BC=DC.又∵CE=CF,∠BCE=∠DCF=90°,∴△BCE≌△DCF.2-1-c-n-j-y
∴∠CBE=∠CDF.又∵∠BEC=∠DEM,∴∠CBE+∠BEC=∠CDF+∠DEM=90°.∴BM⊥DF.21*cnjy*com
(2)解:∵BE平分∠DBC,根据(1)可知:∠BDM=∠F=67.5°,
∴BD=BF,∴DM=FM=DF.
∵正方形ABCD的边长为2,∴BD=BF=2,∴CE=CF=2-2.
在Rt△DCF中,DF2=DC2+CF2=4+(2-2)2=16-8.
∴DM2==4-2.
∵∠CDF=∠CBE=∠DBM,∠DME=∠BMD,
∴△DME∽△BMD.∴=.∴DM2=ME·MB.∴ME·MB=4-2.
16.证明:(1)∵△ABC与△DCE都是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD.
∴△ACE≌△BCD(SAS).
(2)∵△ABC与△DCE都是等边三角形,
∴AB=AC,CD=ED,∠ABC=∠DCE=60°,
∴=,AB∥DC,
∴∠ABG=∠GDC,∠BAG=∠GCD,∴△ABG∽△CDG,
∴=.
同理,=.
∴=.
17.(1)证明:连接OD,OE,ED,如图①.
∵BC与☉O相切于点D,
∴OD⊥BC,∴∠ODB=90°=∠C.∴OD∥AC.
∵∠C=90°,∠B=30°,∴∠A=60°.
又∵OA=OE,
∴△AOE为等边三角形.∴AE=OA=OD.
∴四边形AODE是平行四边形.
又∵OA=OD,∴四边形AODE是菱形.
①
②
(2)解:连接OD,DF,如图②.
设☉O的半径为r,由(1)知OD∥AC,
∴△OBD∽△ABC.
∴=,即=,解得r=.∴☉O的半径为.
∵OD∥AC,∴∠DAC=∠ADO.
∵OA=OD,∴∠ADO=∠DAO.
∴∠DAC=∠DAO.
∵AF是☉O的直径,
∴∠ADF=90°=∠C.
∴△ADC∽△AFD.
∴=.∴AD2=AC·AF.
∵AC=6,AF=×2=,
∴AD2=6×=45.∴AD==3.
18.解:(1)由题意知,MA=x,ON=1.25x.
在Rt△OAB中,由勾股定理,得
OB===5.
如图,作NP⊥OA于点P,则NP∥AB.
∴△OPN∽△OAB.
∴==,即==,
解得OP=x,PN=x,
∴点N的坐标是.
(2)在△OMN中,OM=4-x,OM边上的高PN=x,
∴S=OM·PN=(4-x)·x=-x2+x.
∴S与x之间的函数表达式为S=-x2+x(0配方,得S=-(x-2)2+.
∴当x=2时,S有最大值,最大值是.
(3)存在某一时刻,使△OMN是直角三角形.
理由如下:
①如图①,若∠OMN=90°,则MN∥AB,此时OM=4-x,ON=1.25x.
∵MN∥AB,∴△OMN∽△OAB,
∴=,即=,解得x=2.
①
②
②如图②,若∠ONM=90°,则∠ONM=∠OAB,此时OM=4-x,ON=1.25x.
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴=,即=,解得x=.
综上所述,x的值是2或.
基础训练
知识点1 用两组角判定两三角形相似
1.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中的相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,则下列三角形中,与△BOC一定相似的是( )21·世纪*教育网
A.△ABD B.△DOA C.△ACD D.△ABO
3.如图,在△ABC中,BD,CE是高,则与△BOE相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
4.下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A.∠A=∠A',∠B=∠B'
B.∠C=∠C'=90°,∠A=35°,∠B'=55°
C.∠A=∠B,∠A'=∠B'
D.∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
5.如图,已知∠1=∠2=∠3,则下列表达式正确的是( )
A.= B.=
C.= D.=
6.下列所给两个三角形不一定相似的是( )
A.两个等腰直角三角形
B.两个等边三角形
C.两个直角三角形
D.各有一个角是100°的两个等腰三角形
7.如图,D,E分别在△ABC的边AB,AC上,且∠1=∠2=∠B,则图中相似三角形有( )
A.4对 B.3对 C.2对 D.1对
8.如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②=;③DP2=PH·PB;④=.其中正确的是 .(写出所有正确结论的序号)21cnjy.com
知识点2 用直角三角形判定两三角形相似
9.如图,已知∠ACB=∠ABD=90°,AB=,AC=2,
当AD= 时,△ABD与△BCA相似.?
10.如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
11.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列说法中:
①AC·BC=AB·CD;②AC2=AD·DB;③BC2=BD·BA;④CD2=AD·DB,正确的个数是( )www.21-cn-jy.com
A.1 B.2 C.3 D.4
12.如图,正方形ABCD的边长为1,P是CD边的中点,Q在线段BC上,△ADP与△QCP相似时,求BQ的值.www-2-1-cnjy-com
提升训练
考查角度1 利用相似三角形证比例
13.如图,AD,BE是钝角三角形ABC的边BC,AC上的高,求证:=.
考查角度2 利用比例式求线段的长
14.如图,D是△ABC的边AC上的一点,连接BD.已知
∠ABD=∠C,AB=6,AD=4,求线段CD的长.
考查角度3 利用相似三角形解四边形问题
15.如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于点E,点F是BC延长线上一点,且CE=CF,BE的延长线交DF于点M.
(1)求证:BM⊥DF;
(2)若正方形ABCD的边长为2,求ME·MB.
考查角度4 利用相似三角形解与全等相关的问题
16.如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.
求证:(1)△ACE≌△BCD;
(2)=.
17.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC,AB于点E,F.21世纪教育网版权所有
(1)若∠B=30°,求证:以A,O,D,E为顶点的四边形是菱形;
(2)若AC=6,AB=10,连接AD,求☉O的半径和AD的长.
18.如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动,当两个动点运动了x秒(0
(2)设△OMN的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.21教育网
参考答案
1.【答案】C 2.【答案】B 3.【答案】C
4.【答案】C 5.【答案】C 6.【答案】C
7.【答案】A 8.【答案】①③④
9.【答案】3或3
10.【答案】C
解:连接EF.若四边形EGFH为菱形,则EF⊥GH,假设线段EF,GH交于点O,则O为AC中点,故AO=AC=2,又△ABC∽△AOE,则==,解得AE=5,故选C.21·cn·jy·com
11.【答案】C
12.解:由题意,得∠D=∠C=90°.
①当△ADP∽△PCQ时,=,
即=,得CQ=.
故BQ=1-=.
②当△ADP∽△QCP时,=,
即=,得QC=1,故BQ=0.
所以当△ADP与△QCP相似时,BQ的值为0或.
跳出误区:因为题中∠D=∠C=90°,所以直角三角形相似在对应顺序上有两种可能,即△ADP∽△PCQ或△ADP∽△QCP,此题容易因只考虑一种情况而漏解.2·1·c·n·j·y
13.证明:在△ACD和△BCE中,∵∠D=∠E=90°,∠ACD=∠BCE,∴△ACD∽△BCE,∴=.【来源:21·世纪·教育·网】
14.解:∵∠A=∠A,∠ABD=∠C,
∴△ABD∽△ACB,∴=,∴AB2=AD·AC.
又AB=6,AD=4,∴AC=9,∴CD=AC-AD=5.
15.(1)证明:∵四边形ABCD是正方形,∴BC=DC.又∵CE=CF,∠BCE=∠DCF=90°,∴△BCE≌△DCF.2-1-c-n-j-y
∴∠CBE=∠CDF.又∵∠BEC=∠DEM,∴∠CBE+∠BEC=∠CDF+∠DEM=90°.∴BM⊥DF.21*cnjy*com
(2)解:∵BE平分∠DBC,根据(1)可知:∠BDM=∠F=67.5°,
∴BD=BF,∴DM=FM=DF.
∵正方形ABCD的边长为2,∴BD=BF=2,∴CE=CF=2-2.
在Rt△DCF中,DF2=DC2+CF2=4+(2-2)2=16-8.
∴DM2==4-2.
∵∠CDF=∠CBE=∠DBM,∠DME=∠BMD,
∴△DME∽△BMD.∴=.∴DM2=ME·MB.∴ME·MB=4-2.
16.证明:(1)∵△ABC与△DCE都是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD.
∴△ACE≌△BCD(SAS).
(2)∵△ABC与△DCE都是等边三角形,
∴AB=AC,CD=ED,∠ABC=∠DCE=60°,
∴=,AB∥DC,
∴∠ABG=∠GDC,∠BAG=∠GCD,∴△ABG∽△CDG,
∴=.
同理,=.
∴=.
17.(1)证明:连接OD,OE,ED,如图①.
∵BC与☉O相切于点D,
∴OD⊥BC,∴∠ODB=90°=∠C.∴OD∥AC.
∵∠C=90°,∠B=30°,∴∠A=60°.
又∵OA=OE,
∴△AOE为等边三角形.∴AE=OA=OD.
∴四边形AODE是平行四边形.
又∵OA=OD,∴四边形AODE是菱形.
①
②
(2)解:连接OD,DF,如图②.
设☉O的半径为r,由(1)知OD∥AC,
∴△OBD∽△ABC.
∴=,即=,解得r=.∴☉O的半径为.
∵OD∥AC,∴∠DAC=∠ADO.
∵OA=OD,∴∠ADO=∠DAO.
∴∠DAC=∠DAO.
∵AF是☉O的直径,
∴∠ADF=90°=∠C.
∴△ADC∽△AFD.
∴=.∴AD2=AC·AF.
∵AC=6,AF=×2=,
∴AD2=6×=45.∴AD==3.
18.解:(1)由题意知,MA=x,ON=1.25x.
在Rt△OAB中,由勾股定理,得
OB===5.
如图,作NP⊥OA于点P,则NP∥AB.
∴△OPN∽△OAB.
∴==,即==,
解得OP=x,PN=x,
∴点N的坐标是.
(2)在△OMN中,OM=4-x,OM边上的高PN=x,
∴S=OM·PN=(4-x)·x=-x2+x.
∴S与x之间的函数表达式为S=-x2+x(0
∴当x=2时,S有最大值,最大值是.
(3)存在某一时刻,使△OMN是直角三角形.
理由如下:
①如图①,若∠OMN=90°,则MN∥AB,此时OM=4-x,ON=1.25x.
∵MN∥AB,∴△OMN∽△OAB,
∴=,即=,解得x=2.
①
②
②如图②,若∠ONM=90°,则∠ONM=∠OAB,此时OM=4-x,ON=1.25x.
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴=,即=,解得x=.
综上所述,x的值是2或.
