27.2.2 相似三角形的性质 同步练习
文档属性
| 名称 | 27.2.2 相似三角形的性质 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 545.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览



文档简介
27.2.2 相似三角形的性质
基础训练
知识点1 相似三角形对应线段的比
1.两个相似三角形对应高之比为1∶2,那么它们对应中线之比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
2.顺次连接三角形三边的中点,所构成的三角形与原三角形对应高的比是( )
A.1∶4 B.1∶3 C.1∶ D.1∶2
3.若一个三角形的三边长分别为2 cm,3 cm,4 cm,与它相似的另一个三角形的最短边长为4 cm,则另一个三角形的周长为( )
A.14 cm B.18 cm C.22 cm D.26 cm
4.如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF的长是( )21·cn·jy·com
A. B. C. D.
5.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2∶3,则△ABC与△DEF对应边上的中线的比为___________.?21·世纪*教育网
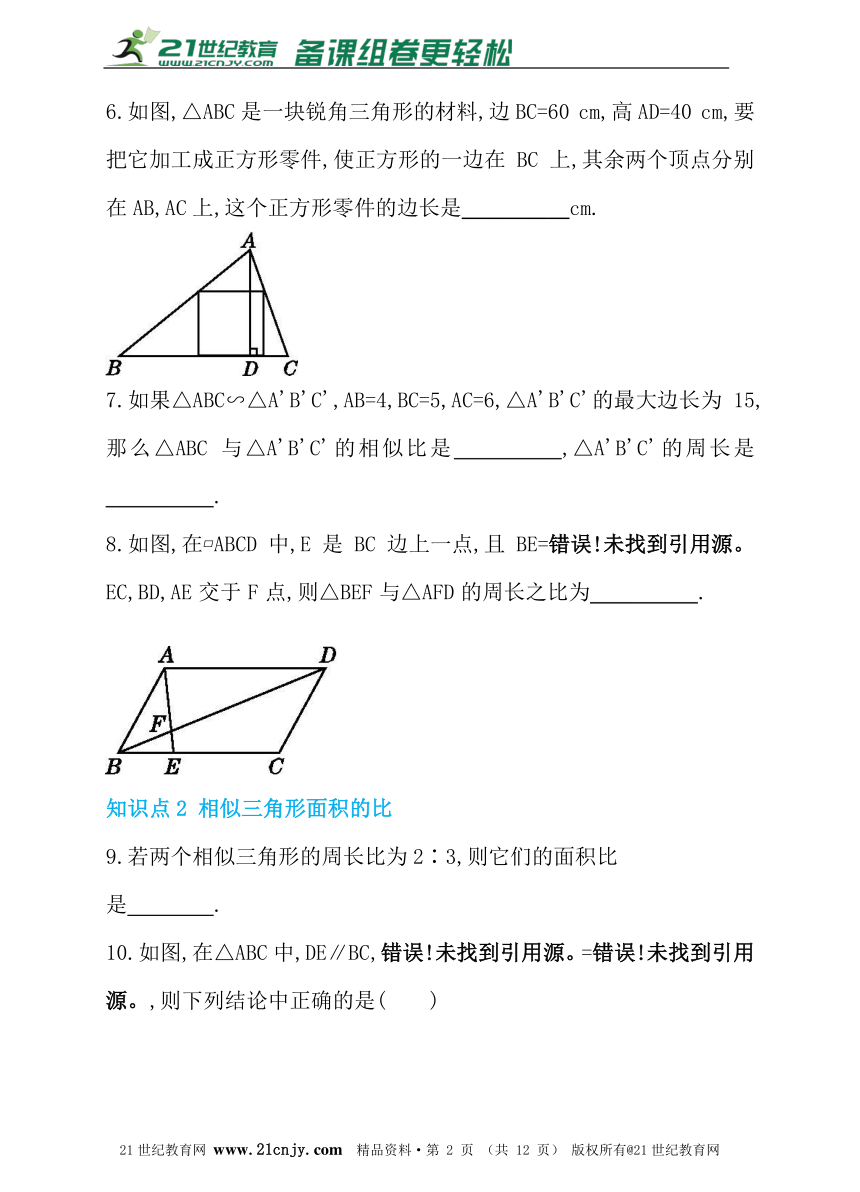
6.如图,△ABC是一块锐角三角形的材料,边BC=60 cm,高AD=40 cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是__________cm.
7.如果△ABC∽△A'B'C',AB=4,BC=5,AC=6,△A'B'C'的最大边长为15,那么△ABC与△A'B'C'的相似比是__________,△A'B'C'的周长是__________.?21*cnjy*com
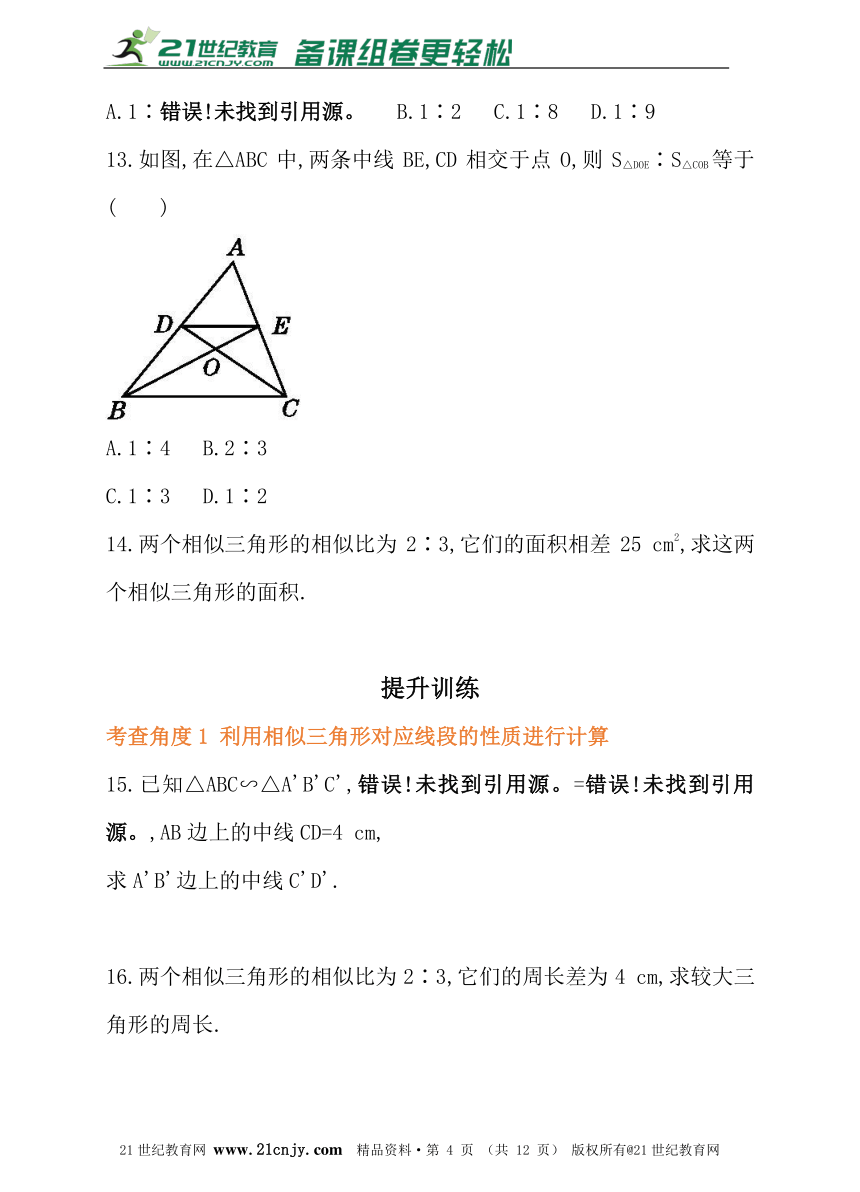
8.如图,在?ABCD中,E是BC边上一点,且BE=EC,BD,AE交于F点,则△BEF与△AFD的周长之比为__________.【出处:21教育名师】
知识点2 相似三角形面积的比
9.若两个相似三角形的周长比为2∶3,则它们的面积比
是 .?
10.如图,在△ABC中,DE∥BC,=,则下列结论中正确的是( )
A.= B.=
C.= D.=
11.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,若
S△BDE∶S△CDE=1∶3,则S△DOE∶S△AOC的值为( )
A. B. C. D.
12.如图,在△ABC中,点D,E分别在边AB,AC上,且==,
则S△ADE∶S四边形BCED等于( )
A.1∶ B.1∶2 C.1∶8 D.1∶9
13.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE∶S△COB等于( )
A.1∶4 B.2∶3
C.1∶3 D.1∶2
14.两个相似三角形的相似比为2∶3,它们的面积相差25 cm2,求这两个相似三角形的面积.
提升训练
考查角度1 利用相似三角形对应线段的性质进行计算
15.已知△ABC∽△A'B'C',=,AB边上的中线CD=4 cm,
求A'B'边上的中线C'D'.
16.两个相似三角形的相似比为2∶3,它们的周长差为4 cm,求较大三角形的周长.
17.如图,在?ABCD中,E是AD边的中点,连接BE并延长交CD延长线于点F,求△EDF与△BCF的周长之比.21教育网
考查角度2 利用相似三角形面积的性质进行计算
18.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,
求△ABC与△DEF的面积之比.
19.如图,在△ABC中,D,E分别为BC,AC边的中点,AD,BE相交于点G,若S△GDE=1,求S△ABC.2·1·c·n·j·y
20.如图,在△ABC中,点D,E分别在边AB,AC上,且==,求S△ADE∶S四边形BCED的值.21cnjy.com
21.如图,☉O是△ABC的外接圆,P是☉O外的一点,AM是☉O的直径,∠PAC=∠ABC.
(1)求证:PA是☉O的切线;
(2)连接PB与AC交于点D,与☉O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证: = = .【来源:21·世纪·教育·网】
22.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A'B'OC'.抛物线y=-x2+2x+3经过点A,C,A'三点.2-1-c-n-j-y
(1)求A,A',C三点的坐标.
(2)求平行四边形ABOC和平行四边形A'B'OC'重叠部分△C'OD的面积.
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA'的面积最大?最大面积是多少?并写出此时M的坐标.【版权所有:21教育】
参考答案
1.【答案】A 2.【答案】D 3.【答案】B
4.【答案】C 5.【答案】2∶3
6.【答案】24 7.【答案】2∶5; 8.【答案】1∶3
9.【答案】4∶9
10.【答案】C 11.【答案】D 12.【答案】C 13.【答案】A
14.解:设这两个相似三角形的面积分别为x cm2和(x+25) cm2.
由题意,得
=,即=.∴x=20,x+25=45,
即这两个相似三角形的面积分别为20 cm2和45 cm2.
易错总结:相似三角形面积的比等于相似比的平方,不与相似比相等,这一点容易出错.
15.解:∵△ABC∽△A'B'C',CD是AB边上的中线,C'D'是A'B'边上的中线,
∴==.又∵CD=4 cm,∴C'D'==×4=6(cm).
即A'B'边上的中线C'D'的长为6 cm.
16.解:由相似比可知两相似三角形的周长比为2∶3,设这两个三角形的周长分别为2x cm,3x cm,则3x-2x=4,解得x=4,则3x=3×4=12.故较大三角形的周长为12 cm.21世纪教育网版权所有
17.解:因为E是AD边的中点,所以AD=2DE,所以===.因为四边形ABCD是平行四边形,所以AD∥BC,所以△EDF∽△BCF,所以△EDF与△BCF的周长之比为1∶2.www.21-cn-jy.com
18.解:根据相似三角形面积的比等于相似比的平方.因为△ABC与△DEF的相似比为3∶4,所以△ABC与△DEF的面积之比为32∶42,即9∶16.www-2-1-cnjy-com
19.解:∵点D,E分别是BC,AC的中点,
∴DE∥AB,DE=AB.
∴△AGB∽△DGE.
∴==22=4.∴S△ABG=4.
∵△AGE与△GDE同高,∴===2,
∴S△AGE=2.
同理可得S△GBD=2,∴S四边形ABDE=4+2+2+1=9.
∵DE∥AB,∴△EDC∽△ABC,设S△ABC=x,
则=,得x=12,即S△ABC=12.
点拨:遇到面积关系问题时,若两三角形相似,则面积比等于相似比的平方;若两三角形不相似但同底或同高,则同高(同底)的两三角形面积比等于底(高)的比.【来源:21cnj*y.co*m】
20.解:因为==,∠A=∠A,所以△AED∽△ABC,所以==,所以S△ABC=4S△AED,S四边形BCED=S△ABC-S△AED=3S△AED,所以S△ADE∶S四边形BCED=1∶3=.
21.证明:(1) 如图,连接CM.
∵∠PAC=∠ABC,∠M=∠ABC,
∴∠PAC=∠M.
∵AM为直径,
∴∠M+∠MAC=90°.
∴∠PAC+∠MAC=90°,
即∠MAP=90°.
∴MA⊥AP.
∴PA是☉O的切线.
(2) 如图,连接AE.
∵M为中点,AM为☉O的直径,
∴AM⊥BC.
∵AM⊥AP,
∴AP∥BC.
∴△ADP∽△CDB.
∴ = .
∵AP∥BC,
∴∠P=∠CBD.
∵∠CBD=∠CAE,
∴∠P=∠CAE.
∵∠P=∠DCF,
∴∠DCF=∠CAE.
又∵∠ADE=∠CDF,∴△ADE∽△CDF.
∴ = ,∴ = = .
22.解:(1)当y=0时,-x2+2x+3=0,
解得x1=3,x2=-1.
∴C(-1,0),A'(3,0).当x=0时,y=3.∴A(0,3).
(2)∵C(-1,0),A(0,3),
∴B(1,3).
∴OB==.
∴△AOB的面积为S=×1×3=.
又∵平行四边形ABOC旋转90°得平行四边形A'B'OC',
∴∠ACO=∠OC'D.
∵∠ACO=∠ABO,
∴∠ABO=∠OC'D.
又∵∠C'OD=∠BOA,
∴△C'OD∽△BOA.
∴===.
∴S△C'OD=.
(3)如图,设M点的坐标为(m,-m2+2m+3),连接AM,A'M,AA',OM.
S△AMA'=S△OA'M+S△OAM-
S△AOA'=×3×(-m2+2m+3)+×3×m-×3×3=-m2+m(0当m=时,S△AMA'取到最大值,为.
此时M的坐标为.
基础训练
知识点1 相似三角形对应线段的比
1.两个相似三角形对应高之比为1∶2,那么它们对应中线之比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
2.顺次连接三角形三边的中点,所构成的三角形与原三角形对应高的比是( )
A.1∶4 B.1∶3 C.1∶ D.1∶2
3.若一个三角形的三边长分别为2 cm,3 cm,4 cm,与它相似的另一个三角形的最短边长为4 cm,则另一个三角形的周长为( )
A.14 cm B.18 cm C.22 cm D.26 cm
4.如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF的长是( )21·cn·jy·com
A. B. C. D.
5.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2∶3,则△ABC与△DEF对应边上的中线的比为___________.?21·世纪*教育网
6.如图,△ABC是一块锐角三角形的材料,边BC=60 cm,高AD=40 cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是__________cm.
7.如果△ABC∽△A'B'C',AB=4,BC=5,AC=6,△A'B'C'的最大边长为15,那么△ABC与△A'B'C'的相似比是__________,△A'B'C'的周长是__________.?21*cnjy*com
8.如图,在?ABCD中,E是BC边上一点,且BE=EC,BD,AE交于F点,则△BEF与△AFD的周长之比为__________.【出处:21教育名师】
知识点2 相似三角形面积的比
9.若两个相似三角形的周长比为2∶3,则它们的面积比
是 .?
10.如图,在△ABC中,DE∥BC,=,则下列结论中正确的是( )
A.= B.=
C.= D.=
11.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,若
S△BDE∶S△CDE=1∶3,则S△DOE∶S△AOC的值为( )
A. B. C. D.
12.如图,在△ABC中,点D,E分别在边AB,AC上,且==,
则S△ADE∶S四边形BCED等于( )
A.1∶ B.1∶2 C.1∶8 D.1∶9
13.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE∶S△COB等于( )
A.1∶4 B.2∶3
C.1∶3 D.1∶2
14.两个相似三角形的相似比为2∶3,它们的面积相差25 cm2,求这两个相似三角形的面积.
提升训练
考查角度1 利用相似三角形对应线段的性质进行计算
15.已知△ABC∽△A'B'C',=,AB边上的中线CD=4 cm,
求A'B'边上的中线C'D'.
16.两个相似三角形的相似比为2∶3,它们的周长差为4 cm,求较大三角形的周长.
17.如图,在?ABCD中,E是AD边的中点,连接BE并延长交CD延长线于点F,求△EDF与△BCF的周长之比.21教育网
考查角度2 利用相似三角形面积的性质进行计算
18.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,
求△ABC与△DEF的面积之比.
19.如图,在△ABC中,D,E分别为BC,AC边的中点,AD,BE相交于点G,若S△GDE=1,求S△ABC.2·1·c·n·j·y
20.如图,在△ABC中,点D,E分别在边AB,AC上,且==,求S△ADE∶S四边形BCED的值.21cnjy.com
21.如图,☉O是△ABC的外接圆,P是☉O外的一点,AM是☉O的直径,∠PAC=∠ABC.
(1)求证:PA是☉O的切线;
(2)连接PB与AC交于点D,与☉O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证: = = .【来源:21·世纪·教育·网】
22.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A'B'OC'.抛物线y=-x2+2x+3经过点A,C,A'三点.2-1-c-n-j-y
(1)求A,A',C三点的坐标.
(2)求平行四边形ABOC和平行四边形A'B'OC'重叠部分△C'OD的面积.
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA'的面积最大?最大面积是多少?并写出此时M的坐标.【版权所有:21教育】
参考答案
1.【答案】A 2.【答案】D 3.【答案】B
4.【答案】C 5.【答案】2∶3
6.【答案】24 7.【答案】2∶5; 8.【答案】1∶3
9.【答案】4∶9
10.【答案】C 11.【答案】D 12.【答案】C 13.【答案】A
14.解:设这两个相似三角形的面积分别为x cm2和(x+25) cm2.
由题意,得
=,即=.∴x=20,x+25=45,
即这两个相似三角形的面积分别为20 cm2和45 cm2.
易错总结:相似三角形面积的比等于相似比的平方,不与相似比相等,这一点容易出错.
15.解:∵△ABC∽△A'B'C',CD是AB边上的中线,C'D'是A'B'边上的中线,
∴==.又∵CD=4 cm,∴C'D'==×4=6(cm).
即A'B'边上的中线C'D'的长为6 cm.
16.解:由相似比可知两相似三角形的周长比为2∶3,设这两个三角形的周长分别为2x cm,3x cm,则3x-2x=4,解得x=4,则3x=3×4=12.故较大三角形的周长为12 cm.21世纪教育网版权所有
17.解:因为E是AD边的中点,所以AD=2DE,所以===.因为四边形ABCD是平行四边形,所以AD∥BC,所以△EDF∽△BCF,所以△EDF与△BCF的周长之比为1∶2.www.21-cn-jy.com
18.解:根据相似三角形面积的比等于相似比的平方.因为△ABC与△DEF的相似比为3∶4,所以△ABC与△DEF的面积之比为32∶42,即9∶16.www-2-1-cnjy-com
19.解:∵点D,E分别是BC,AC的中点,
∴DE∥AB,DE=AB.
∴△AGB∽△DGE.
∴==22=4.∴S△ABG=4.
∵△AGE与△GDE同高,∴===2,
∴S△AGE=2.
同理可得S△GBD=2,∴S四边形ABDE=4+2+2+1=9.
∵DE∥AB,∴△EDC∽△ABC,设S△ABC=x,
则=,得x=12,即S△ABC=12.
点拨:遇到面积关系问题时,若两三角形相似,则面积比等于相似比的平方;若两三角形不相似但同底或同高,则同高(同底)的两三角形面积比等于底(高)的比.【来源:21cnj*y.co*m】
20.解:因为==,∠A=∠A,所以△AED∽△ABC,所以==,所以S△ABC=4S△AED,S四边形BCED=S△ABC-S△AED=3S△AED,所以S△ADE∶S四边形BCED=1∶3=.
21.证明:(1) 如图,连接CM.
∵∠PAC=∠ABC,∠M=∠ABC,
∴∠PAC=∠M.
∵AM为直径,
∴∠M+∠MAC=90°.
∴∠PAC+∠MAC=90°,
即∠MAP=90°.
∴MA⊥AP.
∴PA是☉O的切线.
(2) 如图,连接AE.
∵M为中点,AM为☉O的直径,
∴AM⊥BC.
∵AM⊥AP,
∴AP∥BC.
∴△ADP∽△CDB.
∴ = .
∵AP∥BC,
∴∠P=∠CBD.
∵∠CBD=∠CAE,
∴∠P=∠CAE.
∵∠P=∠DCF,
∴∠DCF=∠CAE.
又∵∠ADE=∠CDF,∴△ADE∽△CDF.
∴ = ,∴ = = .
22.解:(1)当y=0时,-x2+2x+3=0,
解得x1=3,x2=-1.
∴C(-1,0),A'(3,0).当x=0时,y=3.∴A(0,3).
(2)∵C(-1,0),A(0,3),
∴B(1,3).
∴OB==.
∴△AOB的面积为S=×1×3=.
又∵平行四边形ABOC旋转90°得平行四边形A'B'OC',
∴∠ACO=∠OC'D.
∵∠ACO=∠ABO,
∴∠ABO=∠OC'D.
又∵∠C'OD=∠BOA,
∴△C'OD∽△BOA.
∴===.
∴S△C'OD=.
(3)如图,设M点的坐标为(m,-m2+2m+3),连接AM,A'M,AA',OM.
S△AMA'=S△OA'M+S△OAM-
S△AOA'=×3×(-m2+2m+3)+×3×m-×3×3=-m2+m(0
此时M的坐标为.
