27.2.3 相似三角形的应用举例 同步练习
文档属性
| 名称 | 27.2.3 相似三角形的应用举例 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 591.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览



文档简介
27.2.7 相似三角形的应用举例
基础训练
知识点1利用相似测量长度
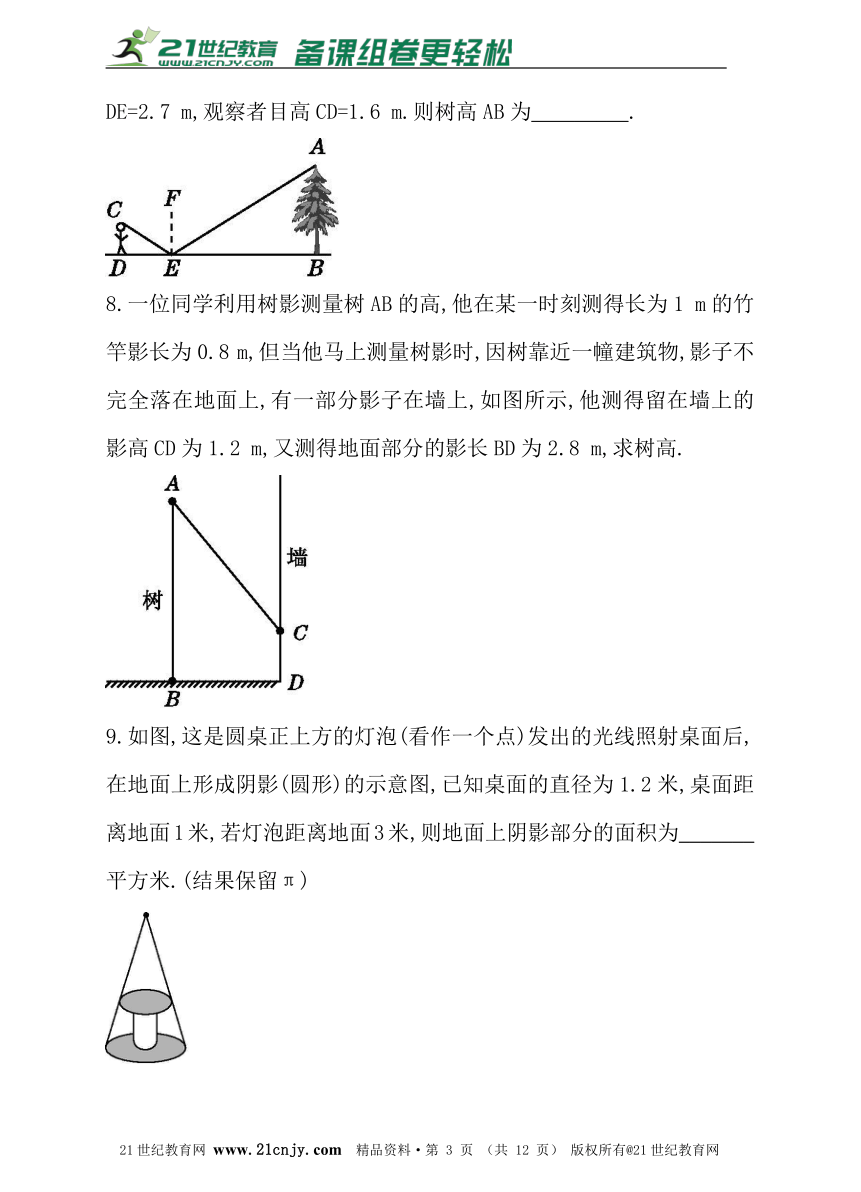
1. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=_________里.?21·cn·jy·com
2.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为__________米.?
知识点2 利用相似测量高度
3.如图,是小孔成像原理的示意图,根据图中所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. cm B. cm C. cm D.4 cm
4.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高为_________米.【来源:21·世纪·教育·网】
5.如图,利用标杆BE测量建筑物的高度,标杆BE高为1.5 m,测得AB=2 m,BC=7 m,则建筑物高CD为_________m.?www-2-1-cnjy-com
6.在同一时刻,高为1.5 m的标杆的影长为2.5 m,一古塔在地面上的影长为50 m,那么古塔的高为_________.?2-1-c-n-j-y
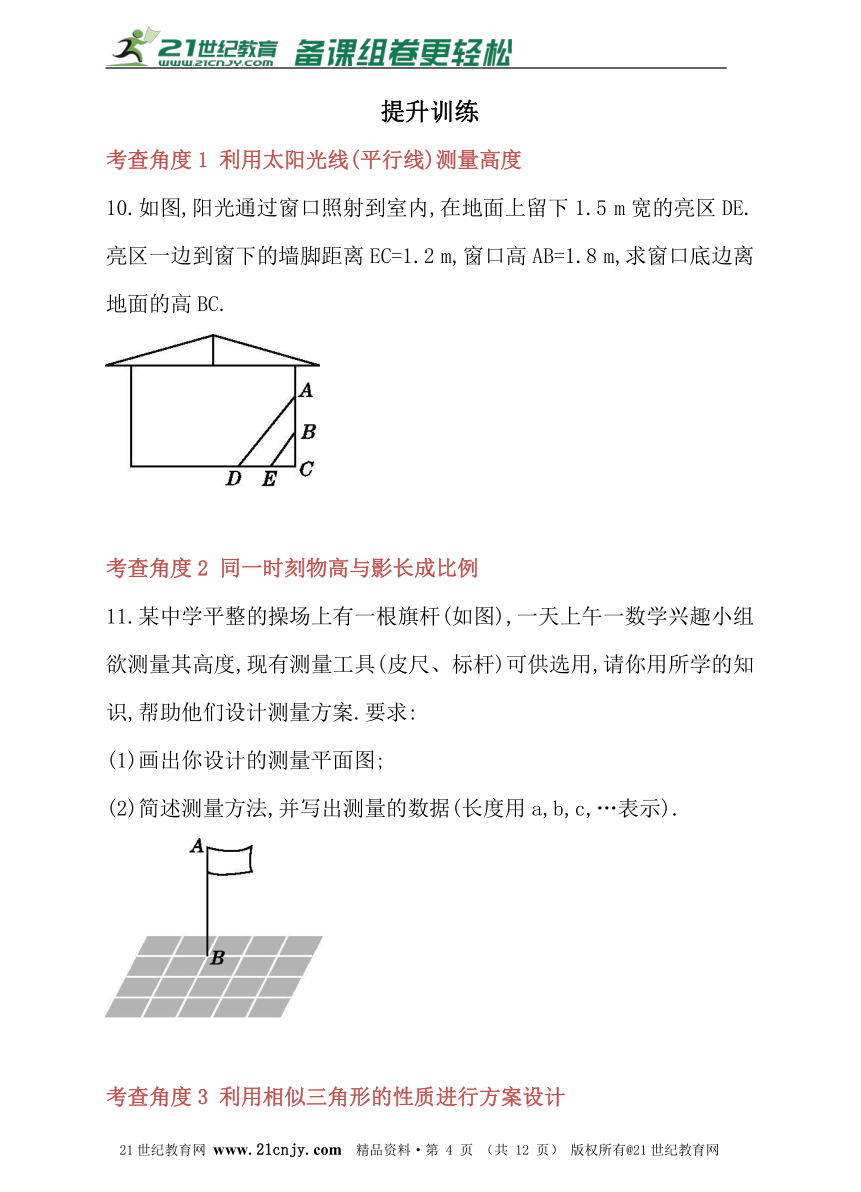
7.为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计了如图所示的测量方案,把镜子放在离树(AB)8.1 m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树顶点A,再用皮尺测量得DE=2.7 m,观察者目高CD=1.6 m.则树高AB为_________.
8.一位同学利用树影测量树AB的高,他在某一时刻测得长为1 m的竹竿影长为0.8 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他测得留在墙上的影高CD为1.2 m,又测得地面部分的影长BD为2.8 m,求树高.
9.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为_______平方米.(结果保留π)21*cnjy*com
提升训练
考查角度1 利用太阳光线(平行线)测量高度
10.如图,阳光通过窗口照射到室内,在地面上留下1.5 m宽的亮区DE.亮区一边到窗下的墙脚距离EC=1.2 m,窗口高AB=1.8 m,求窗口底边离地面的高BC.www.21-cn-jy.com
考查角度2 同一时刻物高与影长成比例
11.某中学平整的操场上有一根旗杆(如图),一天上午一数学兴趣小组欲测量其高度,现有测量工具(皮尺、标杆)可供选用,请你用所学的知识,帮助他们设计测量方案.要求:【来源:21cnj*y.co*m】
(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用a,b,c,…表示).
考查角度3 利用相似三角形的性质进行方案设计
12.如图,我们想要测量河两岸相对两点A,B之间的距离(即河宽),你有什么方法?
考查角度4 借助现有工具构造相似三角形测量高度
13.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高AB.2·1·c·n·j·y
14.某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).【版权所有:21教育】
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.21教育名师原创作品
根据以上测量过程及测量数据,请你求出河宽BD是多少米.
15.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时(身高BN)的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时的身高为1.75 m,求路灯的高CD.(结果精确到0.1 m)
探究培优
拔尖角度 利用相似三角形的性质解决实际生活问题
16.如图①,小红家阳台上放置了一个晒衣架.如图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点位于地面,经测量,AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.21*cnjy*com
(1)求证:AC∥BD;
(2)小红的连衣裙挂在衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.【出处:21教育名师】
参考答案
1.【答案】1.05
2.【答案】5
解:根据题意易得△MBA∽△MCO,根据相似三角形的性质可知=,即=,解得AM=5(米).
3.【答案】D
4.【答案】54
5.【答案】6.75
解:∵EB⊥AC,DC⊥AC,∴EB∥DC,
∴△ABE∽△ACD,∴=.∵BE=1.5 m,AB=2 m,BC=7 m,∴AC=9 m,∴=,∴CD=6.75(m).21·世纪*教育网
6.【答案】30 m
7.【答案】4.8 m
解:利用三角形CDE和三角形ABE相似求解.
8.解:设墙上的影高CD落在地面上时的长度为x m,树高为h m.
∵某一时刻测得长为1 m的竹竿影长为0.8 m,墙上的影高CD为1.2 m,
∴=,解得x=0.96.
∴树的影长为0.96+2.8=3.76(m).
∴=,解得h=4.7.
∴树高为4.7 m.
9.【答案】0.81π
解:容易把对应高的比看成1∶3,另外对应高的比与面积比的关系易搞错.
10.解:作EF⊥DC交AD于F,则EF∥AB.
因为AD∥BE,所以∠FDE=∠BEC.
又因为∠DEF=∠ECB=90°,
所以△DEF∽△ECB,
所以=.
因为AB∥EF,AD∥BE,
所以四边形ABEF是平行四边形,
所以EF=AB=1.8 m.
所以CB===1.44(m).
答:窗口底边离地面的高BC为1.44 m.
解:光线AD∥BE,作EF⊥DC交AD于F,则△DEF∽△ECB,利用边的比例关系求出BC.
11.解:(1)如图,沿着旗杆的影子竖立标杆,使标杆影子的顶端正好与旗杆影子顶端重合.
(2)用皮尺测量旗杆的影长BE=a米,标杆CD的影长DE=b米,标杆高CD=c米.
根据△EDC∽△EBA,得=,即=,所以AB=米.即旗杆AB的高为米.
12.解:方案1:如图①,构造全等三角形.在河岸边作BC⊥AB,在BC上取一点O,使BO=OC,连接AO并延长,过C作BC的垂线交AO的延长线于点D,则△ABO≌△DCO,所以AB=CD.测量出CD的长,即可得到河宽AB.
方案2:如图②,构造相似三角形.在河岸边作BC⊥AB,在BC上取一点O,使BO=2OC,连接AO并延长,过C作BC的垂线交AO的延长线于点D,则△ABO∽△DCO,所以==2,即AB=2CD.测量出CD的长,即可求出河宽AB.21cnjy.com
13.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴=.
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,AC=1.5 m,CD=8 m,
∴=,∴BC=4(m).
∴AB=AC+BC=1.5+4=5.5 (m).
答:树高AB为5.5 m.
14.解:由题意,知∠BAD=∠BCE.
又∵∠ABD=∠ABE=90°,∴△BAD∽△BCE.
∴=,∴=.
∴BD=13.6(米).
答:河宽BD是13.6米.
15.解:设路灯的高CD为x m.
∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,
∴MA∥CD,BN∥CD,EC=CD=x m.
∴△ABN∽△ACD.∴=,
即=.
解得x=6.125≈6.1.
答:路灯的高CD约为6.1 m.
16.(1)证法一:∵AB、CD相交于点O,
∴∠AOC=∠BOD.
∵OA=OC,
∴∠OAC=∠OCA=(180°-∠AOC).
同理可证:∠OBD=∠ODB=(180°-∠BOD).
∴∠OAC=∠OBD.∴AC∥BD.
证法二:∵AB=CD=136 cm,OA=OC=51 cm,
∴OB=OD=85 cm,∴==.
又∵∠AOC=∠BOD,∴△AOC∽△BOD.
∴∠OAC=∠OBD.∴AC∥BD.
(2)解:小红的连衣裙会拖落到地面.
如图,在△OEF中,OE=OF=34 cm,EF=32 cm,作OM⊥EF于点M,则EM=16 cm.21世纪教育网版权所有
在Rt△OEM中,OM===30(cm).
过点A作AH⊥BD于点H,
同(1)可证:EF∥BD,
∴∠ABH=∠OEM,
则Rt△OEM∽Rt△ABH,
∴=,∴AH===120(cm).
∵122>120,∴小红的连衣裙会拖落到地面.
解:(1)根据等边对等角得出∠OAC=∠OCA=(180°-∠AOC)和∠OBD=∠ODB=(180°-∠BOD),进而利用平行线的判定即可证出;
(2)作OM⊥EF于M,AH⊥BD于H,证明Rt△OEM∽Rt△ABH,进而求出AH的长,作比较来判断.21教育网
基础训练
知识点1利用相似测量长度
1. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=_________里.?21·cn·jy·com
2.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为__________米.?
知识点2 利用相似测量高度
3.如图,是小孔成像原理的示意图,根据图中所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. cm B. cm C. cm D.4 cm
4.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高为_________米.【来源:21·世纪·教育·网】
5.如图,利用标杆BE测量建筑物的高度,标杆BE高为1.5 m,测得AB=2 m,BC=7 m,则建筑物高CD为_________m.?www-2-1-cnjy-com
6.在同一时刻,高为1.5 m的标杆的影长为2.5 m,一古塔在地面上的影长为50 m,那么古塔的高为_________.?2-1-c-n-j-y
7.为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计了如图所示的测量方案,把镜子放在离树(AB)8.1 m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树顶点A,再用皮尺测量得DE=2.7 m,观察者目高CD=1.6 m.则树高AB为_________.
8.一位同学利用树影测量树AB的高,他在某一时刻测得长为1 m的竹竿影长为0.8 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他测得留在墙上的影高CD为1.2 m,又测得地面部分的影长BD为2.8 m,求树高.
9.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为_______平方米.(结果保留π)21*cnjy*com
提升训练
考查角度1 利用太阳光线(平行线)测量高度
10.如图,阳光通过窗口照射到室内,在地面上留下1.5 m宽的亮区DE.亮区一边到窗下的墙脚距离EC=1.2 m,窗口高AB=1.8 m,求窗口底边离地面的高BC.www.21-cn-jy.com
考查角度2 同一时刻物高与影长成比例
11.某中学平整的操场上有一根旗杆(如图),一天上午一数学兴趣小组欲测量其高度,现有测量工具(皮尺、标杆)可供选用,请你用所学的知识,帮助他们设计测量方案.要求:【来源:21cnj*y.co*m】
(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用a,b,c,…表示).
考查角度3 利用相似三角形的性质进行方案设计
12.如图,我们想要测量河两岸相对两点A,B之间的距离(即河宽),你有什么方法?
考查角度4 借助现有工具构造相似三角形测量高度
13.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高AB.2·1·c·n·j·y
14.某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).【版权所有:21教育】
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.21教育名师原创作品
根据以上测量过程及测量数据,请你求出河宽BD是多少米.
15.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时(身高BN)的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时的身高为1.75 m,求路灯的高CD.(结果精确到0.1 m)
探究培优
拔尖角度 利用相似三角形的性质解决实际生活问题
16.如图①,小红家阳台上放置了一个晒衣架.如图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点位于地面,经测量,AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.21*cnjy*com
(1)求证:AC∥BD;
(2)小红的连衣裙挂在衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.【出处:21教育名师】
参考答案
1.【答案】1.05
2.【答案】5
解:根据题意易得△MBA∽△MCO,根据相似三角形的性质可知=,即=,解得AM=5(米).
3.【答案】D
4.【答案】54
5.【答案】6.75
解:∵EB⊥AC,DC⊥AC,∴EB∥DC,
∴△ABE∽△ACD,∴=.∵BE=1.5 m,AB=2 m,BC=7 m,∴AC=9 m,∴=,∴CD=6.75(m).21·世纪*教育网
6.【答案】30 m
7.【答案】4.8 m
解:利用三角形CDE和三角形ABE相似求解.
8.解:设墙上的影高CD落在地面上时的长度为x m,树高为h m.
∵某一时刻测得长为1 m的竹竿影长为0.8 m,墙上的影高CD为1.2 m,
∴=,解得x=0.96.
∴树的影长为0.96+2.8=3.76(m).
∴=,解得h=4.7.
∴树高为4.7 m.
9.【答案】0.81π
解:容易把对应高的比看成1∶3,另外对应高的比与面积比的关系易搞错.
10.解:作EF⊥DC交AD于F,则EF∥AB.
因为AD∥BE,所以∠FDE=∠BEC.
又因为∠DEF=∠ECB=90°,
所以△DEF∽△ECB,
所以=.
因为AB∥EF,AD∥BE,
所以四边形ABEF是平行四边形,
所以EF=AB=1.8 m.
所以CB===1.44(m).
答:窗口底边离地面的高BC为1.44 m.
解:光线AD∥BE,作EF⊥DC交AD于F,则△DEF∽△ECB,利用边的比例关系求出BC.
11.解:(1)如图,沿着旗杆的影子竖立标杆,使标杆影子的顶端正好与旗杆影子顶端重合.
(2)用皮尺测量旗杆的影长BE=a米,标杆CD的影长DE=b米,标杆高CD=c米.
根据△EDC∽△EBA,得=,即=,所以AB=米.即旗杆AB的高为米.
12.解:方案1:如图①,构造全等三角形.在河岸边作BC⊥AB,在BC上取一点O,使BO=OC,连接AO并延长,过C作BC的垂线交AO的延长线于点D,则△ABO≌△DCO,所以AB=CD.测量出CD的长,即可得到河宽AB.
方案2:如图②,构造相似三角形.在河岸边作BC⊥AB,在BC上取一点O,使BO=2OC,连接AO并延长,过C作BC的垂线交AO的延长线于点D,则△ABO∽△DCO,所以==2,即AB=2CD.测量出CD的长,即可求出河宽AB.21cnjy.com
13.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴=.
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,AC=1.5 m,CD=8 m,
∴=,∴BC=4(m).
∴AB=AC+BC=1.5+4=5.5 (m).
答:树高AB为5.5 m.
14.解:由题意,知∠BAD=∠BCE.
又∵∠ABD=∠ABE=90°,∴△BAD∽△BCE.
∴=,∴=.
∴BD=13.6(米).
答:河宽BD是13.6米.
15.解:设路灯的高CD为x m.
∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,
∴MA∥CD,BN∥CD,EC=CD=x m.
∴△ABN∽△ACD.∴=,
即=.
解得x=6.125≈6.1.
答:路灯的高CD约为6.1 m.
16.(1)证法一:∵AB、CD相交于点O,
∴∠AOC=∠BOD.
∵OA=OC,
∴∠OAC=∠OCA=(180°-∠AOC).
同理可证:∠OBD=∠ODB=(180°-∠BOD).
∴∠OAC=∠OBD.∴AC∥BD.
证法二:∵AB=CD=136 cm,OA=OC=51 cm,
∴OB=OD=85 cm,∴==.
又∵∠AOC=∠BOD,∴△AOC∽△BOD.
∴∠OAC=∠OBD.∴AC∥BD.
(2)解:小红的连衣裙会拖落到地面.
如图,在△OEF中,OE=OF=34 cm,EF=32 cm,作OM⊥EF于点M,则EM=16 cm.21世纪教育网版权所有
在Rt△OEM中,OM===30(cm).
过点A作AH⊥BD于点H,
同(1)可证:EF∥BD,
∴∠ABH=∠OEM,
则Rt△OEM∽Rt△ABH,
∴=,∴AH===120(cm).
∵122>120,∴小红的连衣裙会拖落到地面.
解:(1)根据等边对等角得出∠OAC=∠OCA=(180°-∠AOC)和∠OBD=∠ODB=(180°-∠BOD),进而利用平行线的判定即可证出;
(2)作OM⊥EF于M,AH⊥BD于H,证明Rt△OEM∽Rt△ABH,进而求出AH的长,作比较来判断.21教育网
