27.3.1 位似图形 同步练习
图片预览

文档简介
27.3.1 位似图形
基础训练
知识点1 位似图形的定义
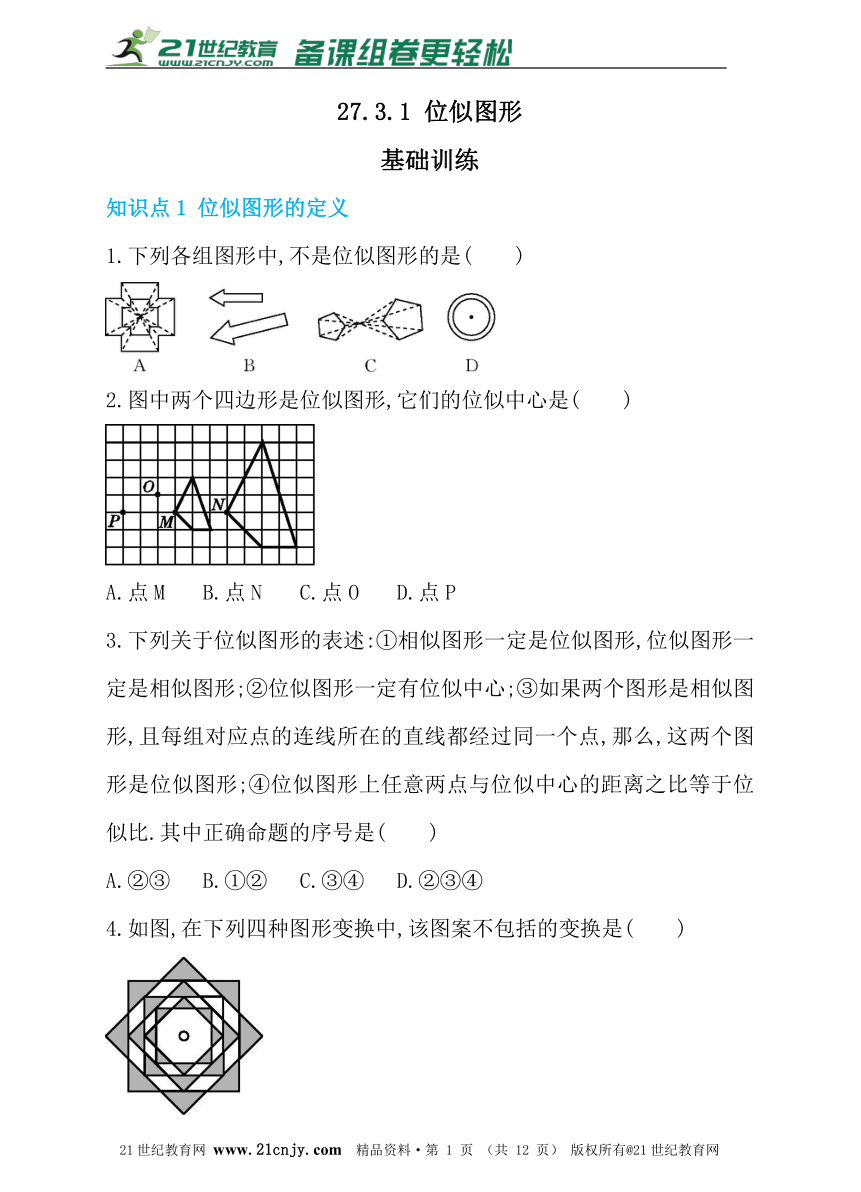
1.下列各组图形中,不是位似图形的是( )
2.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
3.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是( )2-1-c-n-j-y
A.②③ B.①② C.③④ D.②③④
4.如图,在下列四种图形变换中,该图案不包括的变换是( )
A.平移 B.轴对称 C.旋转 D.位似
5.如图,△OAB和△OCD是位似图形,则位似中心是_________,图中AB与CD的位置关系是_________.21cnjy.com
知识点2位似图形的性质
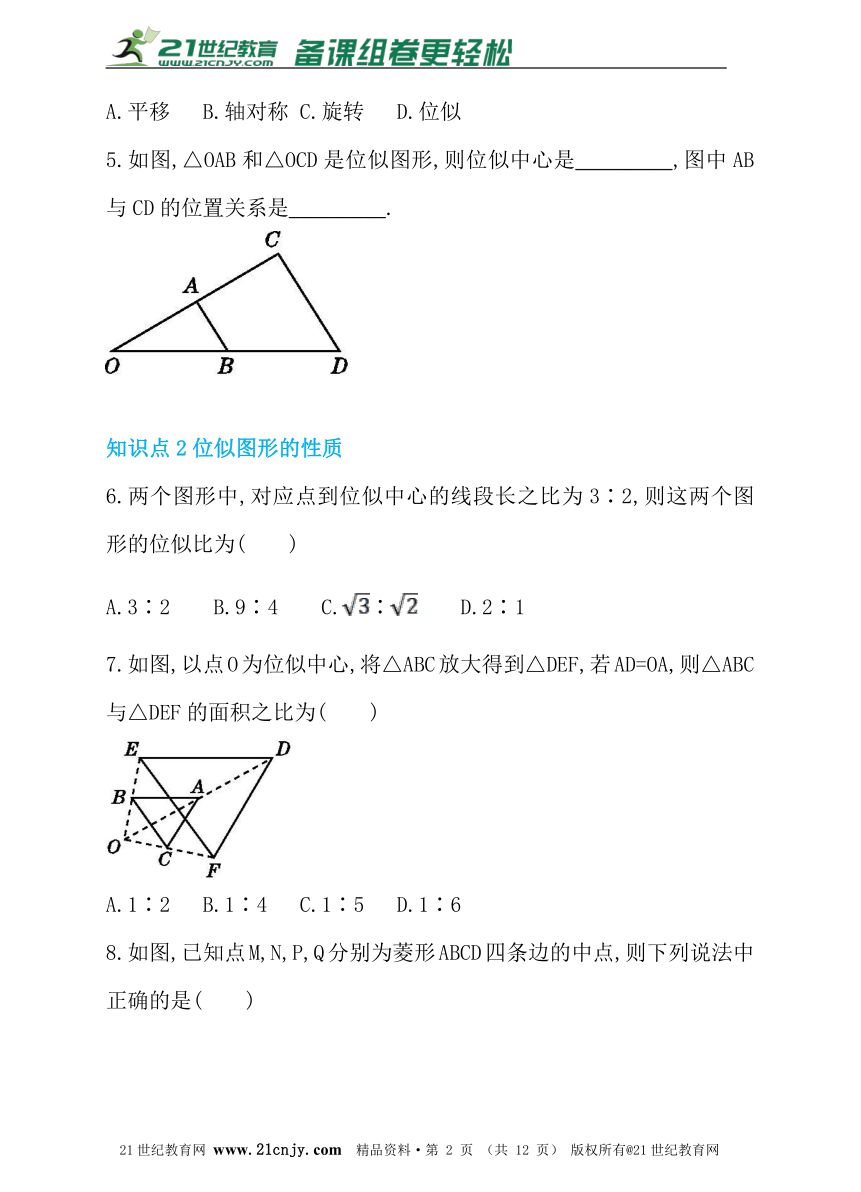
6.两个图形中,对应点到位似中心的线段长之比为3∶2,则这两个图形的位似比为( )
A.3∶2 B.9∶4 C.∶ D.2∶1
7.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为( )【来源:21cnj*y.co*m】
A.1∶2 B.1∶4 C.1∶5 D.1∶6
8.如图,已知点M,N,P,Q分别为菱形ABCD四条边的中点,则下列说法中正确的是( )
A.四边形MNPQ是菱形
B.四边形MNPQ与菱形ABCD位似
C.四边形MNPQ与菱形ABCD的周长之比为1∶2
D.四边形MNPQ与菱形ABCD的面积之比为1∶2
知识点3 位似图形的画法
9.下面是△ABC位似图形的几种画法,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )
A.图形外 B.图形内
C.图形上 D.以上都可以
11.如图,在正方形ABCD的边AB,BC,CD,DA上顺次截取
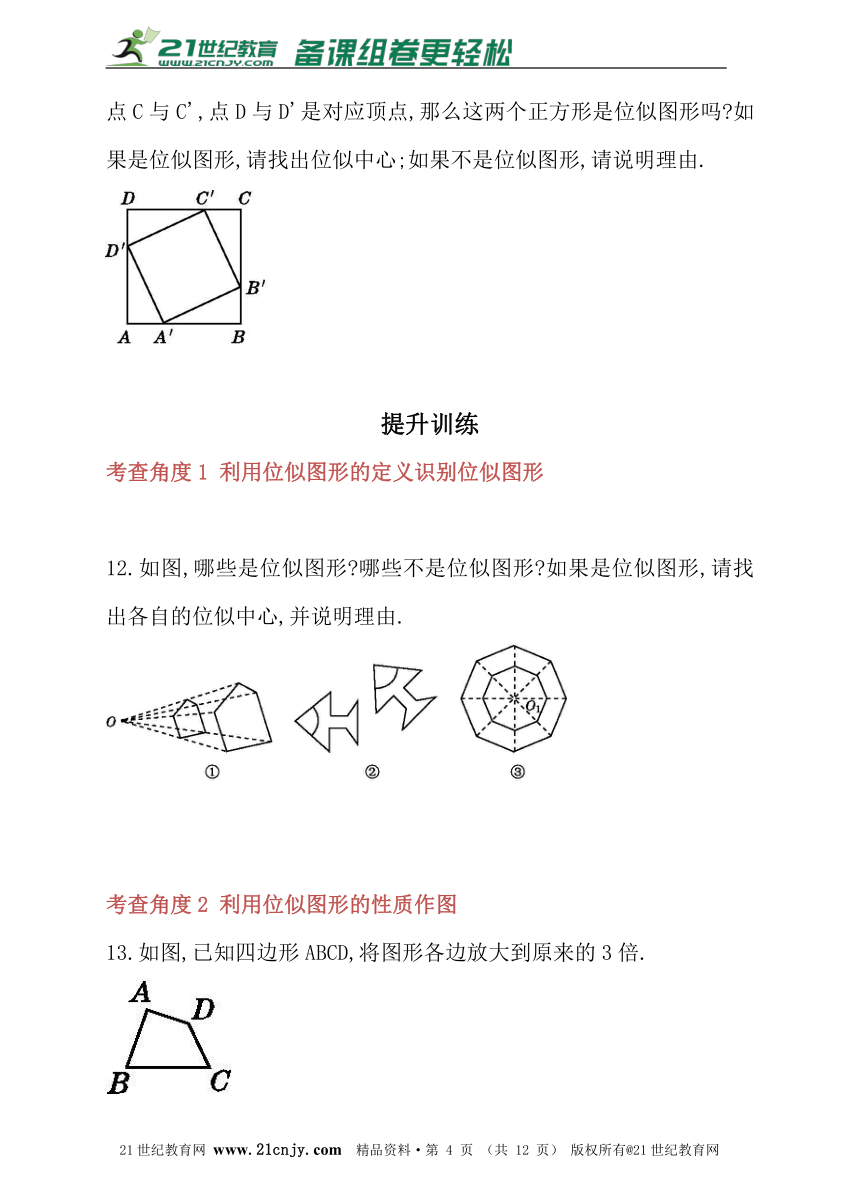
AA'=BB'=CC'=DD',根据所学知识,我们知道四边形A'B'C'D'也是正方形,且正方形A'B'C'D'相似于正方形ABCD,其中点A与A',点B与B',点C与C',点D与D'是对应顶点,那么这两个正方形是位似图形吗?如果是位似图形,请找出位似中心;如果不是位似图形,请说明理由.
提升训练
考查角度1 利用位似图形的定义识别位似图形
12.如图,哪些是位似图形?哪些不是位似图形?如果是位似图形,请找出各自的位似中心,并说明理由.
考查角度2 利用位似图形的性质作图
13.如图,已知四边形ABCD,将图形各边放大到原来的3倍.
考查角度3 利用位似图形进行相关计算
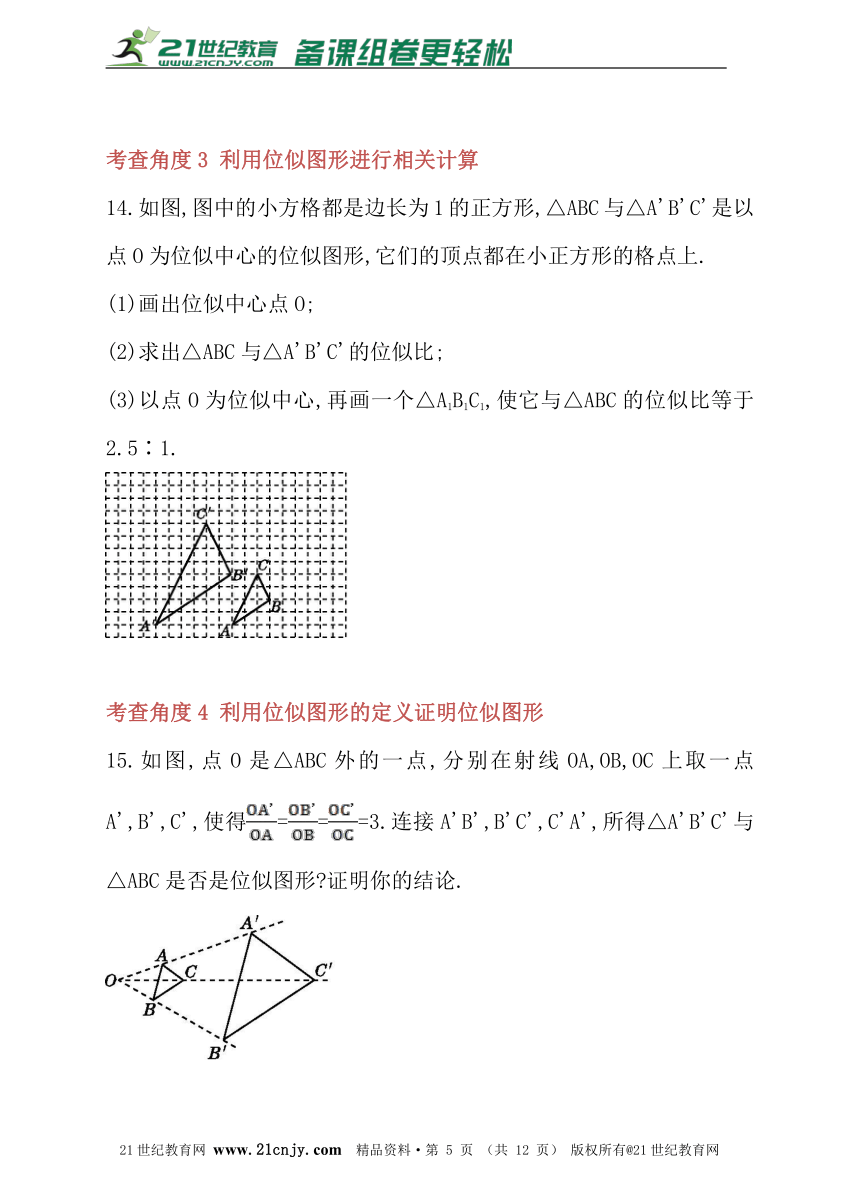
14.如图,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于2.5∶1.
考查角度4 利用位似图形的定义证明位似图形
15.如图,点O是△ABC外的一点,分别在射线OA,OB,OC上取一点A',B',C',使得===3.连接A'B',B'C',C'A',所得△A'B'C'与△ABC是否是位似图形?证明你的结论.21世纪教育网版权所有
考查角度5 利用位似图形的性质求线段长(方程思想)
16.如图,矩形ABCD与矩形AB'C'D'是位似图形,A为位似中心.已知矩形ABCD的周长为24,BB'=4,DD'=2,求AB,AD的长.www-2-1-cnjy-com
探究培优
拔尖角度1 利用位似图形性质证等积式
17.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形.
求证:OD·OC=OF·OA.
拔尖角度2 利用位似图形的性质判断线段的位置关系
18.如图,△ABC与△A'B'C'是位似图形,点A,B,A',B',O共线,点O为位似中心.
(1)AC与A'C'平行吗?为什么?
(2)若AB=2A'B',OC'=5,求CC'的长.
拔尖角度3 利用位似图形的定义和性质探究与位似相关的问题
19.如图,在所给网格图(每个小正方形的边长是1)中完成下列问题:
(1)四边形ABCD与四边形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M,N;21教育网
(2)以图中O点为位似中心,将四边形ABCD放大,得到放大后的四边形A2B2C2D2,求四边形ABCD与四边形A2B2C2D2的对应边的比是多少.
(3)求四边形A2B2C2D2的面积.
参考答案
1.【答案】B 2.【答案】D 3.【答案】D
4.【答案】A 5.【答案】点O;平行 6.【答案】A
7.【答案】B 8.【答案】D 9.【答案】C 10.【答案】D
11.解:这两个正方形不是位似图形,因为它们对应点的连线所在的直线不交于同一点.
易错总结:两个图形是位似图形的条件是:(1)它们是相似图形;(2)两个图形的对应点所在的直线相交于一点,即位似中心.本题中的两个正方形虽是相似图形,但无论顶点间是怎样的对应关系,其连线所在的直线都不交于同一点,因此它们不是位似图形.21·世纪*教育网
12.解:①③两组中的图形是位似图形,它们的位似中心分别为点O,O1.理由如下:根据位似图形的概念,如果两个图形不仅是相似图形,而且每组对应点所在的直线都相交于一点,那么这样的两个图形叫做位似图形.图①③都具备这个特点,而②中的两个图形不具备这个特点,所以②不是位似图形.【来源:21·世纪·教育·网】
方法总结:识别位似图形的方法:先判断两个图形是否相似,如果不是相似图形,则这两个图形不可能位似;如果相似,再判断这两个相似图形的每组对应点所在的直线是否都经过同一个点,若经过,可判断两个图形位似,否则两个图形不位似.21*cnjy*com
13.解:方法一:位似中心在图形外,在图形的外面任选一点O,如图①.
(1)作射线OA,OB,OC,OD,在这些射线上分别截取
OA'=3OA,OB'=3OB,OC'=3OC,OD'=3OD.
(2)顺次连接A',B',C',D',所得图形A'B'C'D'即为所求.
方法二:位似中心在图形上,例如:以点B为位似中心,如图②.
(1)延长BA,BC分别到A',C',使BA'=3BA,
BC'=3BC.
(2)连接BD并延长到D',使BD'=3BD.
(3)连接A'D',D'C',所得图形A'BC'D'即为所求.
方法三:位似中心在图形内,在图形的内部任选一点O.请同学们自己试着做一做.
点拨:作位似图形,关键是先选定位似中心的位置.
14.解:(1)位似中心点O如图所示.
(2)由图易知,OA=6,OA'=12,
∴==,
∴△ABC与△A'B'C'的位似比为1∶2.
(3)△A1B1C1如图所示.
15.解:△A'B'C'与△ABC是位似图形.
证明如下:由已知得===3,
∠AOC=∠A'OC',∴△AOC∽△A'OC'.
∴=.同理,△OBC∽△OB'C',
△OAB∽△OA'B',
∴=,=.
∴==.
∴△A'B'C'∽△ABC.又直线AA',BB',CC'交于一点,
∴△A'B'C'与△ABC是位似图形.
16.解:设AB=x,AD=y,由矩形ABCD的周长为24,得2(x+y)=24①.又∵矩形ABCD与矩形AB'C'D'位似,∴=,即=②.解由①②组成的方程组得即AB,AD的长分别为8和4.www.21-cn-jy.com
17.证明:∵△DEO与△ABO是位似图形,∴=.
又∵△OEF与△OBC是位似图形,
∴=.∴=,
即OD·OC=OF·OA.
18.解:(1)AC与A'C'平行.
理由:∵△ABC与△A'B'C'是位似图形,∴AC与A'C'为对应边,由位似的性质可知AC∥A'C'.21·cn·jy·com
(2)∵△ABC与△A'B'C'是位似图形,∴△ABC∽△A'B'C',
∵AB=2A'B',
∴AC=2A'C'.又∵点A,B,A',B',O共线,AC∥A'C',
∴△OAC∽△OA'C'.∴OC=2OC'.
又∵OC'=5,∴OC=10.∴CC'=OC-OC'=10-5=5.
19.解:(1)直线MN如图所示.
(2)易知
AB=3,BC=,CD=,AD=,A2B2=6,B2C2=2,C2D2=2,A2D2=2,所以====,即四边形ABCD与四边形A2B2C2D2对应边的比为1∶2.2·1·c·n·j·y
(3)=-=×8×6-×8×2=16.
基础训练
知识点1 位似图形的定义
1.下列各组图形中,不是位似图形的是( )
2.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
3.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是( )2-1-c-n-j-y
A.②③ B.①② C.③④ D.②③④
4.如图,在下列四种图形变换中,该图案不包括的变换是( )
A.平移 B.轴对称 C.旋转 D.位似
5.如图,△OAB和△OCD是位似图形,则位似中心是_________,图中AB与CD的位置关系是_________.21cnjy.com
知识点2位似图形的性质
6.两个图形中,对应点到位似中心的线段长之比为3∶2,则这两个图形的位似比为( )
A.3∶2 B.9∶4 C.∶ D.2∶1
7.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为( )【来源:21cnj*y.co*m】
A.1∶2 B.1∶4 C.1∶5 D.1∶6
8.如图,已知点M,N,P,Q分别为菱形ABCD四条边的中点,则下列说法中正确的是( )
A.四边形MNPQ是菱形
B.四边形MNPQ与菱形ABCD位似
C.四边形MNPQ与菱形ABCD的周长之比为1∶2
D.四边形MNPQ与菱形ABCD的面积之比为1∶2
知识点3 位似图形的画法
9.下面是△ABC位似图形的几种画法,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )
A.图形外 B.图形内
C.图形上 D.以上都可以
11.如图,在正方形ABCD的边AB,BC,CD,DA上顺次截取
AA'=BB'=CC'=DD',根据所学知识,我们知道四边形A'B'C'D'也是正方形,且正方形A'B'C'D'相似于正方形ABCD,其中点A与A',点B与B',点C与C',点D与D'是对应顶点,那么这两个正方形是位似图形吗?如果是位似图形,请找出位似中心;如果不是位似图形,请说明理由.
提升训练
考查角度1 利用位似图形的定义识别位似图形
12.如图,哪些是位似图形?哪些不是位似图形?如果是位似图形,请找出各自的位似中心,并说明理由.
考查角度2 利用位似图形的性质作图
13.如图,已知四边形ABCD,将图形各边放大到原来的3倍.
考查角度3 利用位似图形进行相关计算
14.如图,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于2.5∶1.
考查角度4 利用位似图形的定义证明位似图形
15.如图,点O是△ABC外的一点,分别在射线OA,OB,OC上取一点A',B',C',使得===3.连接A'B',B'C',C'A',所得△A'B'C'与△ABC是否是位似图形?证明你的结论.21世纪教育网版权所有
考查角度5 利用位似图形的性质求线段长(方程思想)
16.如图,矩形ABCD与矩形AB'C'D'是位似图形,A为位似中心.已知矩形ABCD的周长为24,BB'=4,DD'=2,求AB,AD的长.www-2-1-cnjy-com
探究培优
拔尖角度1 利用位似图形性质证等积式
17.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形.
求证:OD·OC=OF·OA.
拔尖角度2 利用位似图形的性质判断线段的位置关系
18.如图,△ABC与△A'B'C'是位似图形,点A,B,A',B',O共线,点O为位似中心.
(1)AC与A'C'平行吗?为什么?
(2)若AB=2A'B',OC'=5,求CC'的长.
拔尖角度3 利用位似图形的定义和性质探究与位似相关的问题
19.如图,在所给网格图(每个小正方形的边长是1)中完成下列问题:
(1)四边形ABCD与四边形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M,N;21教育网
(2)以图中O点为位似中心,将四边形ABCD放大,得到放大后的四边形A2B2C2D2,求四边形ABCD与四边形A2B2C2D2的对应边的比是多少.
(3)求四边形A2B2C2D2的面积.
参考答案
1.【答案】B 2.【答案】D 3.【答案】D
4.【答案】A 5.【答案】点O;平行 6.【答案】A
7.【答案】B 8.【答案】D 9.【答案】C 10.【答案】D
11.解:这两个正方形不是位似图形,因为它们对应点的连线所在的直线不交于同一点.
易错总结:两个图形是位似图形的条件是:(1)它们是相似图形;(2)两个图形的对应点所在的直线相交于一点,即位似中心.本题中的两个正方形虽是相似图形,但无论顶点间是怎样的对应关系,其连线所在的直线都不交于同一点,因此它们不是位似图形.21·世纪*教育网
12.解:①③两组中的图形是位似图形,它们的位似中心分别为点O,O1.理由如下:根据位似图形的概念,如果两个图形不仅是相似图形,而且每组对应点所在的直线都相交于一点,那么这样的两个图形叫做位似图形.图①③都具备这个特点,而②中的两个图形不具备这个特点,所以②不是位似图形.【来源:21·世纪·教育·网】
方法总结:识别位似图形的方法:先判断两个图形是否相似,如果不是相似图形,则这两个图形不可能位似;如果相似,再判断这两个相似图形的每组对应点所在的直线是否都经过同一个点,若经过,可判断两个图形位似,否则两个图形不位似.21*cnjy*com
13.解:方法一:位似中心在图形外,在图形的外面任选一点O,如图①.
(1)作射线OA,OB,OC,OD,在这些射线上分别截取
OA'=3OA,OB'=3OB,OC'=3OC,OD'=3OD.
(2)顺次连接A',B',C',D',所得图形A'B'C'D'即为所求.
方法二:位似中心在图形上,例如:以点B为位似中心,如图②.
(1)延长BA,BC分别到A',C',使BA'=3BA,
BC'=3BC.
(2)连接BD并延长到D',使BD'=3BD.
(3)连接A'D',D'C',所得图形A'BC'D'即为所求.
方法三:位似中心在图形内,在图形的内部任选一点O.请同学们自己试着做一做.
点拨:作位似图形,关键是先选定位似中心的位置.
14.解:(1)位似中心点O如图所示.
(2)由图易知,OA=6,OA'=12,
∴==,
∴△ABC与△A'B'C'的位似比为1∶2.
(3)△A1B1C1如图所示.
15.解:△A'B'C'与△ABC是位似图形.
证明如下:由已知得===3,
∠AOC=∠A'OC',∴△AOC∽△A'OC'.
∴=.同理,△OBC∽△OB'C',
△OAB∽△OA'B',
∴=,=.
∴==.
∴△A'B'C'∽△ABC.又直线AA',BB',CC'交于一点,
∴△A'B'C'与△ABC是位似图形.
16.解:设AB=x,AD=y,由矩形ABCD的周长为24,得2(x+y)=24①.又∵矩形ABCD与矩形AB'C'D'位似,∴=,即=②.解由①②组成的方程组得即AB,AD的长分别为8和4.www.21-cn-jy.com
17.证明:∵△DEO与△ABO是位似图形,∴=.
又∵△OEF与△OBC是位似图形,
∴=.∴=,
即OD·OC=OF·OA.
18.解:(1)AC与A'C'平行.
理由:∵△ABC与△A'B'C'是位似图形,∴AC与A'C'为对应边,由位似的性质可知AC∥A'C'.21·cn·jy·com
(2)∵△ABC与△A'B'C'是位似图形,∴△ABC∽△A'B'C',
∵AB=2A'B',
∴AC=2A'C'.又∵点A,B,A',B',O共线,AC∥A'C',
∴△OAC∽△OA'C'.∴OC=2OC'.
又∵OC'=5,∴OC=10.∴CC'=OC-OC'=10-5=5.
19.解:(1)直线MN如图所示.
(2)易知
AB=3,BC=,CD=,AD=,A2B2=6,B2C2=2,C2D2=2,A2D2=2,所以====,即四边形ABCD与四边形A2B2C2D2对应边的比为1∶2.2·1·c·n·j·y
(3)=-=×8×6-×8×2=16.
