27.3.2 平面直角坐标系中的位似 同步练习
文档属性
| 名称 | 27.3.2 平面直角坐标系中的位似 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 756.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览



文档简介
27.3.2 平面直角坐标系中的位似
基础训练
知识点1 平面直角坐标系中点的位似
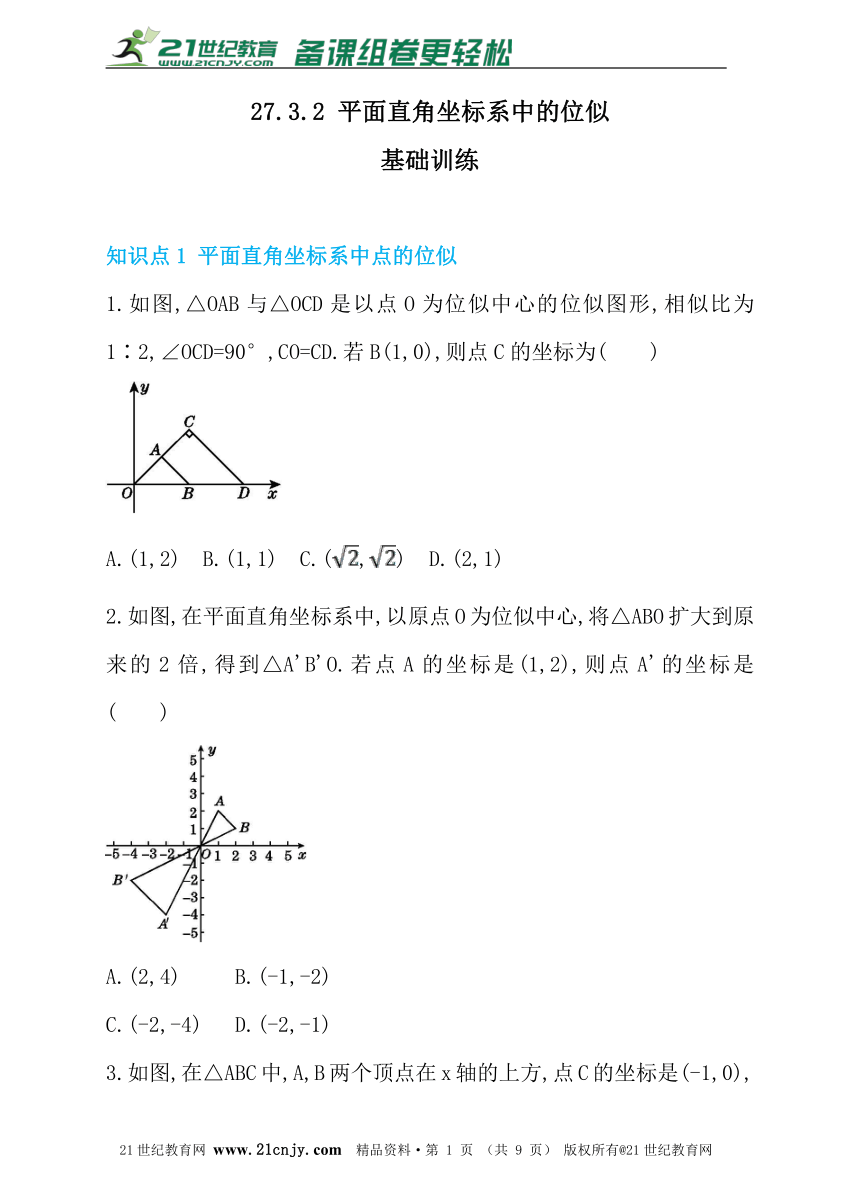
1.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2) B.(1,1) C.(,) D.(2,1)
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A'B'O.若点A的坐标是(1,2),则点A'的坐标是( )21教育网
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
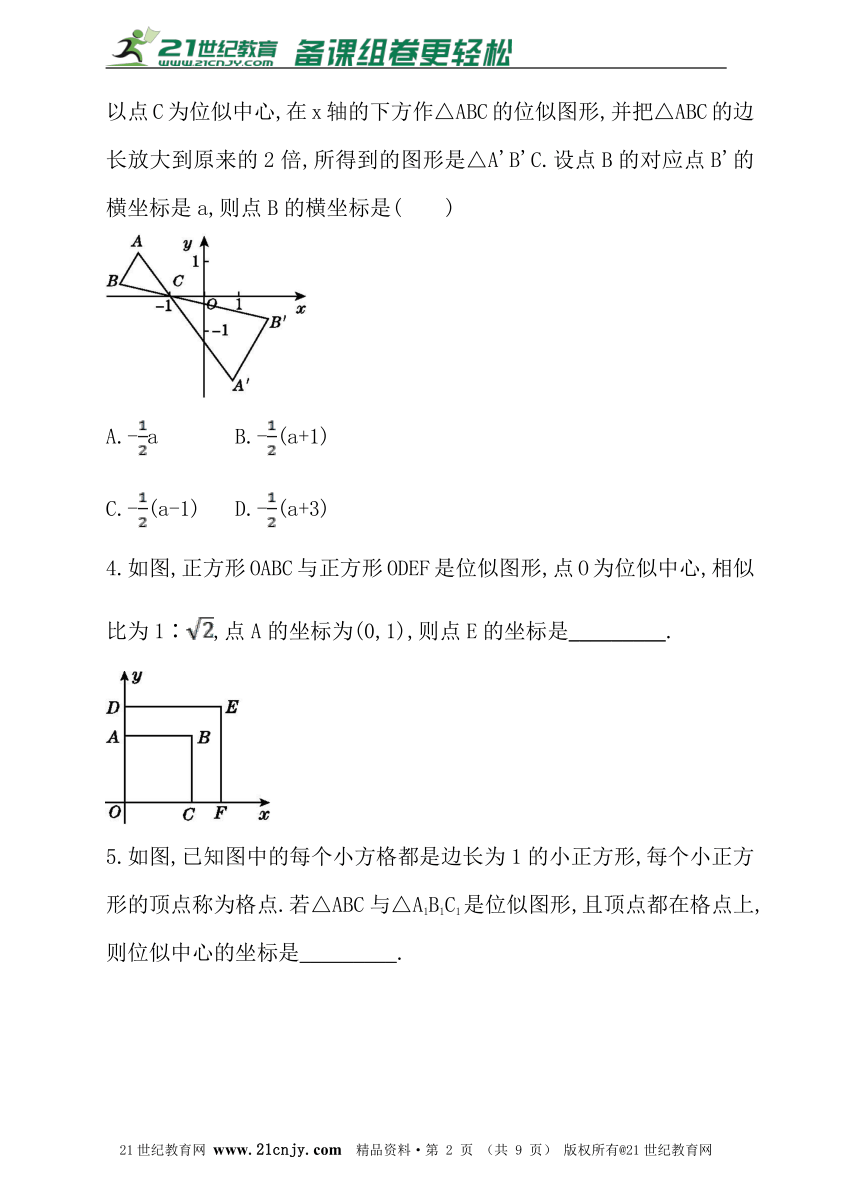
3.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,所得到的图形是△A'B'C.设点B的对应点B'的横坐标是a,则点B的横坐标是( )21cnjy.com
A.-a B.-(a+1)
C.-(a-1) D.-(a+3)
4.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标是_________.
5.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是_________.【来源:21·世纪·教育·网】
知识点2 位似在坐标系中的简单应用
6.人们给电脑屏幕也建立了坐标系,如果把电脑屏幕的左上角定为坐标原点(0,0),右下角的点的坐标是(640,-480),则屏幕正中央的点的坐标是_________.?21·世纪*教育网
7.如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶
点”的坐标为(a,b) ,那么大“鱼”上对应“顶点”的坐标为( )
A.(-a,-2b) B.(-2a,-b)
C.(-2a,-2b) D.(-2b,-2a)
8.如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A'B'C'D'与正方形ABCD是以AC的中点O'为中心的位似图形.已知AC=3,若点A'的坐标为(1,2),则正方形A'B'C'D'与正方形ABCD的相似比是( )www-2-1-cnjy-com
A. B. C. D.
9.如图,将△ABC以点G为位似中心缩小到原来的,得到△A'B'C',写出变化前后两个三角形各顶点的坐标.2-1-c-n-j-y
10.在13×13的网格中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2∶1,画出△ABC的位似图形△A'B'C';
(2)写出△A'B'C'的各顶点坐标.
11.如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使△A2B2C2与△ABC位似且=.21世纪教育网版权所有
提升训练
考查角度1 在坐标平面内作位似图形并求其面积(割补法)
12.如图,已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).在正方形网格中,每个小正方形的边长是1个单位长度.21·cn·jy·com
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2∶1,并直接写出C2点的坐标及△A2BC2的面积.
考查角度2 位似图形与一次函数的综合应用(函数思想、数形结合思想)
13.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),求这两个正方形的位似中心的坐标.
参考答案
1.【答案】B 2.【答案】C 3.【答案】D
4.【答案】(,)
5.【答案】(9,0)
6.【答案】(320,-240) 7.【答案】C 8.【答案】B
9.解:△ABC的各顶点坐标分别为A(0,0),B(5,2),C(0,4),G点坐标为(-2,0).∵△ABC以点G为位似中心缩小到原来的,得到△A'B'C',∴△A'B'C'的各顶点坐标分别为A'(-1,0),B'(1.5,1),C'(-1,2).
误区诊断:应用坐标变化规律时容易忽视前提条件,而以坐标原点为位似中心.在这个问题中,位似中心是点G(-2,0),而非原点,所以不能直接将坐标缩为原来的.www.21-cn-jy.com
10.解:(1)如图所示,△A'B'C'即为所求;
(2)△A'B'C'的各顶点坐标分别为:A'(3,6),B'(5,2),C'(11,4).
11.解:(1)如图所示,△A1B1C1即为所求.△A1B1C1的各顶点坐标为:A1(1,-3),B1(4,-2),C1(2,-1).2·1·c·n·j·y
(2)如图所示,△A2B2C2即为所求.
12.解:(1)△A1B1C1如图所示,C1(2,-2);
(2)△A2BC2如图所示,C2(1,0),=10.
13.解:①当两个位似图形在位似中心同旁时,连接CF,位似中心就是直线CF与x轴的交点.
设直线CF的解析式为y=kx+b,将点C(4,2),F(1,1)的坐标代入,得
解得
故直线CF的解析式为y=x+.
当y=0时,x=-2,所以直线CF交x轴于点(-2,0),即位似中心为点(-2,0).
②当位似中心在两个正方形之间时,易知直线OC的解析式为y=x,直线BG的解析式为y=-x+1.
联立解得
即位似中心为.
综上所述,这两个正方形的位似中心的坐标为(-2,0)或.
基础训练
知识点1 平面直角坐标系中点的位似
1.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2) B.(1,1) C.(,) D.(2,1)
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A'B'O.若点A的坐标是(1,2),则点A'的坐标是( )21教育网
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
3.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,所得到的图形是△A'B'C.设点B的对应点B'的横坐标是a,则点B的横坐标是( )21cnjy.com
A.-a B.-(a+1)
C.-(a-1) D.-(a+3)
4.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标是_________.
5.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是_________.【来源:21·世纪·教育·网】
知识点2 位似在坐标系中的简单应用
6.人们给电脑屏幕也建立了坐标系,如果把电脑屏幕的左上角定为坐标原点(0,0),右下角的点的坐标是(640,-480),则屏幕正中央的点的坐标是_________.?21·世纪*教育网
7.如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶
点”的坐标为(a,b) ,那么大“鱼”上对应“顶点”的坐标为( )
A.(-a,-2b) B.(-2a,-b)
C.(-2a,-2b) D.(-2b,-2a)
8.如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A'B'C'D'与正方形ABCD是以AC的中点O'为中心的位似图形.已知AC=3,若点A'的坐标为(1,2),则正方形A'B'C'D'与正方形ABCD的相似比是( )www-2-1-cnjy-com
A. B. C. D.
9.如图,将△ABC以点G为位似中心缩小到原来的,得到△A'B'C',写出变化前后两个三角形各顶点的坐标.2-1-c-n-j-y
10.在13×13的网格中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2∶1,画出△ABC的位似图形△A'B'C';
(2)写出△A'B'C'的各顶点坐标.
11.如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使△A2B2C2与△ABC位似且=.21世纪教育网版权所有
提升训练
考查角度1 在坐标平面内作位似图形并求其面积(割补法)
12.如图,已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).在正方形网格中,每个小正方形的边长是1个单位长度.21·cn·jy·com
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2∶1,并直接写出C2点的坐标及△A2BC2的面积.
考查角度2 位似图形与一次函数的综合应用(函数思想、数形结合思想)
13.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),求这两个正方形的位似中心的坐标.
参考答案
1.【答案】B 2.【答案】C 3.【答案】D
4.【答案】(,)
5.【答案】(9,0)
6.【答案】(320,-240) 7.【答案】C 8.【答案】B
9.解:△ABC的各顶点坐标分别为A(0,0),B(5,2),C(0,4),G点坐标为(-2,0).∵△ABC以点G为位似中心缩小到原来的,得到△A'B'C',∴△A'B'C'的各顶点坐标分别为A'(-1,0),B'(1.5,1),C'(-1,2).
误区诊断:应用坐标变化规律时容易忽视前提条件,而以坐标原点为位似中心.在这个问题中,位似中心是点G(-2,0),而非原点,所以不能直接将坐标缩为原来的.www.21-cn-jy.com
10.解:(1)如图所示,△A'B'C'即为所求;
(2)△A'B'C'的各顶点坐标分别为:A'(3,6),B'(5,2),C'(11,4).
11.解:(1)如图所示,△A1B1C1即为所求.△A1B1C1的各顶点坐标为:A1(1,-3),B1(4,-2),C1(2,-1).2·1·c·n·j·y
(2)如图所示,△A2B2C2即为所求.
12.解:(1)△A1B1C1如图所示,C1(2,-2);
(2)△A2BC2如图所示,C2(1,0),=10.
13.解:①当两个位似图形在位似中心同旁时,连接CF,位似中心就是直线CF与x轴的交点.
设直线CF的解析式为y=kx+b,将点C(4,2),F(1,1)的坐标代入,得
解得
故直线CF的解析式为y=x+.
当y=0时,x=-2,所以直线CF交x轴于点(-2,0),即位似中心为点(-2,0).
②当位似中心在两个正方形之间时,易知直线OC的解析式为y=x,直线BG的解析式为y=-x+1.
联立解得
即位似中心为.
综上所述,这两个正方形的位似中心的坐标为(-2,0)或.
