27.1.1 相似图形与比例线段 同步练习
文档属性
| 名称 | 27.1.1 相似图形与比例线段 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 437.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-28 00:00:00 | ||
图片预览



文档简介
27.1.1 相似图形与比例线段
基础训练
知识点1 相似图形
1.放大镜中的三角形与原三角形的关系是( )
A.形状不同,大小不同 B.形状相同,大小相同
C.形状相同,大小不同 D.形状不同,大小相同
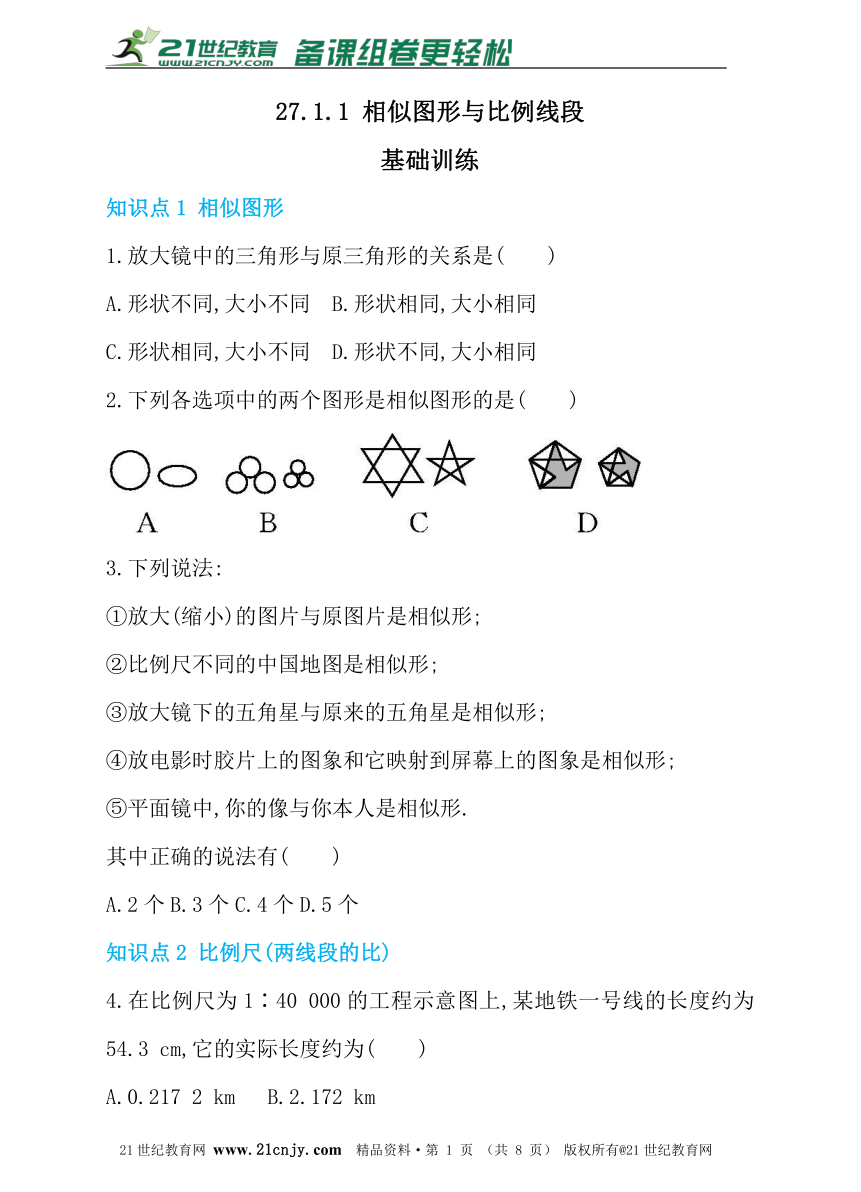
2.下列各选项中的两个图形是相似图形的是( )
3.下列说法:
①放大(缩小)的图片与原图片是相似形;
②比例尺不同的中国地图是相似形;
③放大镜下的五角星与原来的五角星是相似形;
④放电影时胶片上的图象和它映射到屏幕上的图象是相似形;
⑤平面镜中,你的像与你本人是相似形.
其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个
知识点2 比例尺(两线段的比)
4.在比例尺为1∶40 000的工程示意图上,某地铁一号线的长度约为54.3 cm,它的实际长度约为( )
A.0.217 2 km B.2.172 km
C.21.72 km D.217.2 km
5.某机器零件在图纸上的长度是21 mm,它的实际长度是630 mm,则图纸的比例尺是( )
A.1∶20 B.1∶30
C.1∶40 D.1∶50
6.正方形的对角线的长与它的边长之比是( )
A.2∶1 B.1∶2
C.1∶ D.∶1
7.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
知识点3 成比例的线段
8.下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4 B.1,2,2,4
C.3,5,9,13 D.1,2,2,3
9.四条线段a,b,c,d是成比例线段,且=,其中a=3 cm,d=4 cm,c=6 cm,则b等于( )
A.8 cm B. cm C. cm D.2 cm
10.已知三个数1,2,,请你再添上一个数,使它们能构成一个比例式,则这个数是_____________.?
知识点4 比例性质(补充)
11.已知=,那么=( )
A. B. C. D.
12.已知=,则的值是( )
A. B. C. D.
13.如果===k(b+d+f≠0),且a+c+e=3(b+d+f),那么
k=_____________.?
14.已知线段a=3,b=5,c=7.试求a,b,c的第四比例项x.
提升训练
考查角度1 利用相似图形的定义识别相似图形
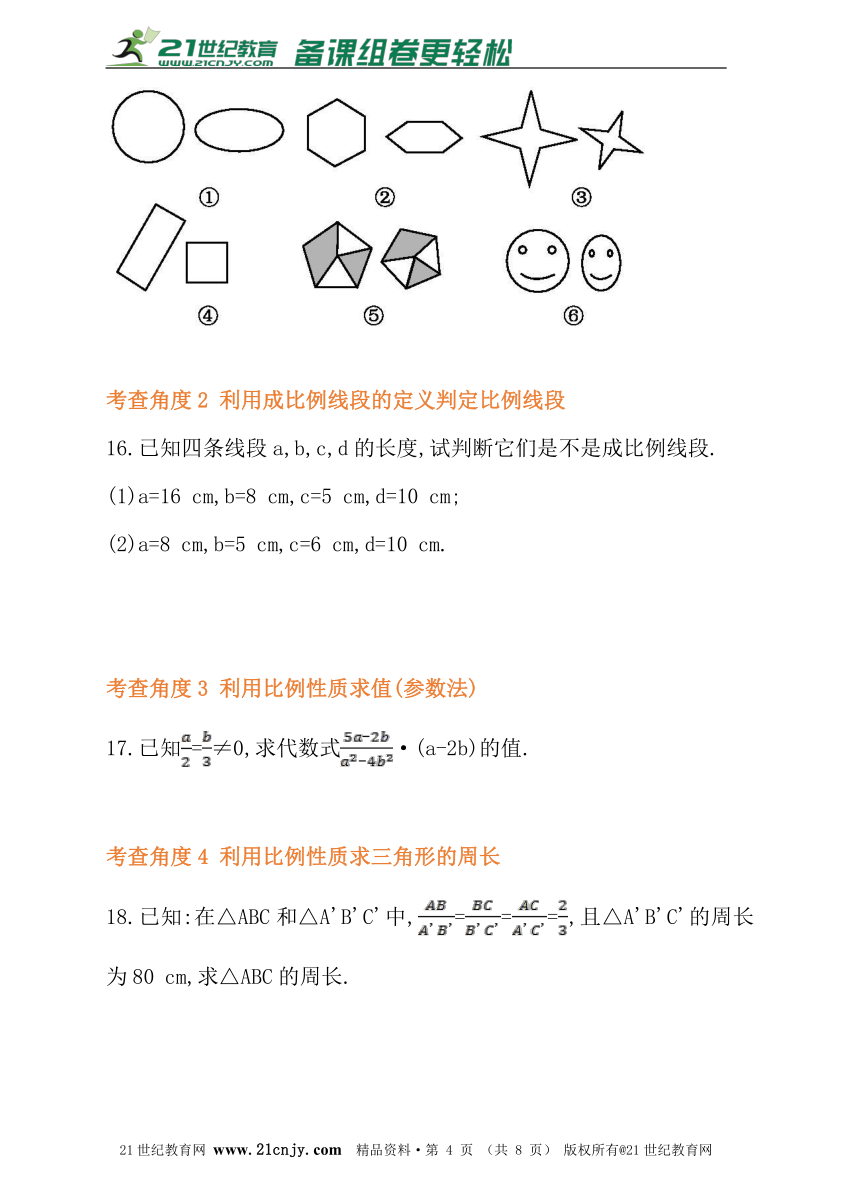
15.如图,各组中的两个图形,哪些是相似的图形,哪些不是?
考查角度2 利用成比例线段的定义判定比例线段
16.已知四条线段a,b,c,d的长度,试判断它们是不是成比例线段.
(1)a=16 cm,b=8 cm,c=5 cm,d=10 cm;
(2)a=8 cm,b=5 cm,c=6 cm,d=10 cm.
考查角度3 利用比例性质求值(参数法)
17.已知=≠0,求代数式·(a-2b)的值.
考查角度4 利用比例性质求三角形的周长
18.已知:在△ABC和△A'B'C'中,===,且△A'B'C'的周长为80 cm,求△ABC的周长.
探究培优
拔尖角度1 利用成比例线段求一线段与已知三线段为成比例线段(分类讨论思想)
19.已知三条线段的长分别为1 cm,4 cm,9 cm,请你再添加一条线段,使这四条线段为成比例线段,求所添加的线段的长.
拔尖角度2 利用比例的性质解决有关三角形的问题
20.设a,b,c是△ABC的三条边,且==,判断△ABC为何种三角形,并说明理由.
参考答案
1.【答案】C
解:放大镜改变物体的大小,不改变物体的形状.放大镜中的三角形与原三角形相似.
2.【答案】D
3.【答案】D
解:①放大(缩小)的图片与原图片是相似形,正确;②比例尺不同的中国地图是相似形,正确;③放大镜下的五角星与原来的五角星是相似形,正确;④放电影时胶片上的图象和它映射到屏幕上的图象是相似形,正确;⑤平面镜中,你的像与你本人是相同的,故是相似形正确.综上所述,正确说法有①②③④⑤,共5个.故选D.
4.【答案】C 5.【答案】B 6.【答案】D
7.【答案】A 8.【答案】B 9.【答案】D
10.【答案】2(答案不唯一) 11.【答案】D
12.【答案】D
解:可以利用代入消元法,也可以用特殊值法求解.因为=,所以不妨设a为13,b为5,则===,故选D.
13.【答案】3
解:利用等比性质时,要注意分母不为零.合理运用比例性质,可以简化计算,根据不同的条件应该灵活选用适当的方法,不要拘泥于一种解题方法.
14.解:根据题意有四条线段a,b,c,x成比例,且a∶b=c∶x,
∴x=.又∵a=3,b=5,c=7,∴x==.
易错总结:要求a,b,c的第四比例项x,就表示四条线段a,b,c,x成比例,且a∶b=c∶x,所以x=,就是说解此题得讲究一个顺序性,解题时容易忽略了这一点.
15.解:图①中两个图形一个是圆,一个是椭圆,形状不同,不相似;图②中两个图形一个是正六边形,一个是任意六边形,形状不同,不相似;图③中两个图形形状相同,相似;图④中两个图形一个是长方形,一个是正方形,形状不同,不相似;图⑤中两个图形形状相同,相似;图⑥中两个图形一个是圆脸,一个是扁脸,形状不同,不相似.综上所述,图③和图⑤是相似的图形,图①②④⑥不是相似的图形.
16.解:(1)∵8×10=80,16×5=80,∴ac=bd,∴a,b,c,d是成比例线段.
(2)∵8×6=48,10×5=50,∴a,b,c,d不是成比例线段.
解:在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.
17.解:∵=,∴3a=2b.
原式=·(a-2b)
=
===.
18.解:∵===,
∴=.
∵△A'B'C'的周长=A'B'+B'C'+A'C'=80 cm,
∴△ABC的周长=AB+BC+AC=(A'B'+B'C'+A'C')=×80=(cm).
19.解:设所添加线段的长为x cm,
当1∶4=9∶x时,解得x=36;
当1∶4=x∶9时,解得x=;
当x∶1=4∶9时,解得x=.
答:所添加线段的长为36 cm或 cm或 cm.
20.解:△ABC为等边三角形.理由如下:
∵a,b,c是△ABC的三条边,∴a+b+c≠0.
∵==,
∴====0,
∴a=b=c,∴△ABC为等边三角形.
解:根据等比性质可得====0,则a=b=c,从而判断出△ABC为等边三角形.
基础训练
知识点1 相似图形
1.放大镜中的三角形与原三角形的关系是( )
A.形状不同,大小不同 B.形状相同,大小相同
C.形状相同,大小不同 D.形状不同,大小相同
2.下列各选项中的两个图形是相似图形的是( )
3.下列说法:
①放大(缩小)的图片与原图片是相似形;
②比例尺不同的中国地图是相似形;
③放大镜下的五角星与原来的五角星是相似形;
④放电影时胶片上的图象和它映射到屏幕上的图象是相似形;
⑤平面镜中,你的像与你本人是相似形.
其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个
知识点2 比例尺(两线段的比)
4.在比例尺为1∶40 000的工程示意图上,某地铁一号线的长度约为54.3 cm,它的实际长度约为( )
A.0.217 2 km B.2.172 km
C.21.72 km D.217.2 km
5.某机器零件在图纸上的长度是21 mm,它的实际长度是630 mm,则图纸的比例尺是( )
A.1∶20 B.1∶30
C.1∶40 D.1∶50
6.正方形的对角线的长与它的边长之比是( )
A.2∶1 B.1∶2
C.1∶ D.∶1
7.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
知识点3 成比例的线段
8.下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4 B.1,2,2,4
C.3,5,9,13 D.1,2,2,3
9.四条线段a,b,c,d是成比例线段,且=,其中a=3 cm,d=4 cm,c=6 cm,则b等于( )
A.8 cm B. cm C. cm D.2 cm
10.已知三个数1,2,,请你再添上一个数,使它们能构成一个比例式,则这个数是_____________.?
知识点4 比例性质(补充)
11.已知=,那么=( )
A. B. C. D.
12.已知=,则的值是( )
A. B. C. D.
13.如果===k(b+d+f≠0),且a+c+e=3(b+d+f),那么
k=_____________.?
14.已知线段a=3,b=5,c=7.试求a,b,c的第四比例项x.
提升训练
考查角度1 利用相似图形的定义识别相似图形
15.如图,各组中的两个图形,哪些是相似的图形,哪些不是?
考查角度2 利用成比例线段的定义判定比例线段
16.已知四条线段a,b,c,d的长度,试判断它们是不是成比例线段.
(1)a=16 cm,b=8 cm,c=5 cm,d=10 cm;
(2)a=8 cm,b=5 cm,c=6 cm,d=10 cm.
考查角度3 利用比例性质求值(参数法)
17.已知=≠0,求代数式·(a-2b)的值.
考查角度4 利用比例性质求三角形的周长
18.已知:在△ABC和△A'B'C'中,===,且△A'B'C'的周长为80 cm,求△ABC的周长.
探究培优
拔尖角度1 利用成比例线段求一线段与已知三线段为成比例线段(分类讨论思想)
19.已知三条线段的长分别为1 cm,4 cm,9 cm,请你再添加一条线段,使这四条线段为成比例线段,求所添加的线段的长.
拔尖角度2 利用比例的性质解决有关三角形的问题
20.设a,b,c是△ABC的三条边,且==,判断△ABC为何种三角形,并说明理由.
参考答案
1.【答案】C
解:放大镜改变物体的大小,不改变物体的形状.放大镜中的三角形与原三角形相似.
2.【答案】D
3.【答案】D
解:①放大(缩小)的图片与原图片是相似形,正确;②比例尺不同的中国地图是相似形,正确;③放大镜下的五角星与原来的五角星是相似形,正确;④放电影时胶片上的图象和它映射到屏幕上的图象是相似形,正确;⑤平面镜中,你的像与你本人是相同的,故是相似形正确.综上所述,正确说法有①②③④⑤,共5个.故选D.
4.【答案】C 5.【答案】B 6.【答案】D
7.【答案】A 8.【答案】B 9.【答案】D
10.【答案】2(答案不唯一) 11.【答案】D
12.【答案】D
解:可以利用代入消元法,也可以用特殊值法求解.因为=,所以不妨设a为13,b为5,则===,故选D.
13.【答案】3
解:利用等比性质时,要注意分母不为零.合理运用比例性质,可以简化计算,根据不同的条件应该灵活选用适当的方法,不要拘泥于一种解题方法.
14.解:根据题意有四条线段a,b,c,x成比例,且a∶b=c∶x,
∴x=.又∵a=3,b=5,c=7,∴x==.
易错总结:要求a,b,c的第四比例项x,就表示四条线段a,b,c,x成比例,且a∶b=c∶x,所以x=,就是说解此题得讲究一个顺序性,解题时容易忽略了这一点.
15.解:图①中两个图形一个是圆,一个是椭圆,形状不同,不相似;图②中两个图形一个是正六边形,一个是任意六边形,形状不同,不相似;图③中两个图形形状相同,相似;图④中两个图形一个是长方形,一个是正方形,形状不同,不相似;图⑤中两个图形形状相同,相似;图⑥中两个图形一个是圆脸,一个是扁脸,形状不同,不相似.综上所述,图③和图⑤是相似的图形,图①②④⑥不是相似的图形.
16.解:(1)∵8×10=80,16×5=80,∴ac=bd,∴a,b,c,d是成比例线段.
(2)∵8×6=48,10×5=50,∴a,b,c,d不是成比例线段.
解:在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.
17.解:∵=,∴3a=2b.
原式=·(a-2b)
=
===.
18.解:∵===,
∴=.
∵△A'B'C'的周长=A'B'+B'C'+A'C'=80 cm,
∴△ABC的周长=AB+BC+AC=(A'B'+B'C'+A'C')=×80=(cm).
19.解:设所添加线段的长为x cm,
当1∶4=9∶x时,解得x=36;
当1∶4=x∶9时,解得x=;
当x∶1=4∶9时,解得x=.
答:所添加线段的长为36 cm或 cm或 cm.
20.解:△ABC为等边三角形.理由如下:
∵a,b,c是△ABC的三条边,∴a+b+c≠0.
∵==,
∴====0,
∴a=b=c,∴△ABC为等边三角形.
解:根据等比性质可得====0,则a=b=c,从而判断出△ABC为等边三角形.
