北师大七年级数学下4.1《认识三角形》习题含详细答案
文档属性
| 名称 | 北师大七年级数学下4.1《认识三角形》习题含详细答案 |  | |
| 格式 | zip | ||
| 文件大小 | 165.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-01 16:51:32 | ||
图片预览

文档简介
《认识三角形》习题
一、选择题
1.一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法判定
2.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm
B.5cm,6cm,10cm
C.1cm,1cm,3cm
D.3cm,4cm,9cm
3.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
4.作△ABC的边AB上的高,下列作法中,正确的是( )
5.若直角三角形中的两个锐角之差为22°,则较小的一个锐角的度数是(
)
A.24°
B.34°
C.44°
D.46°
6.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是(
)
A.120°
B.90°
C.60°
D.30°
二、填空题
7.在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
8.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
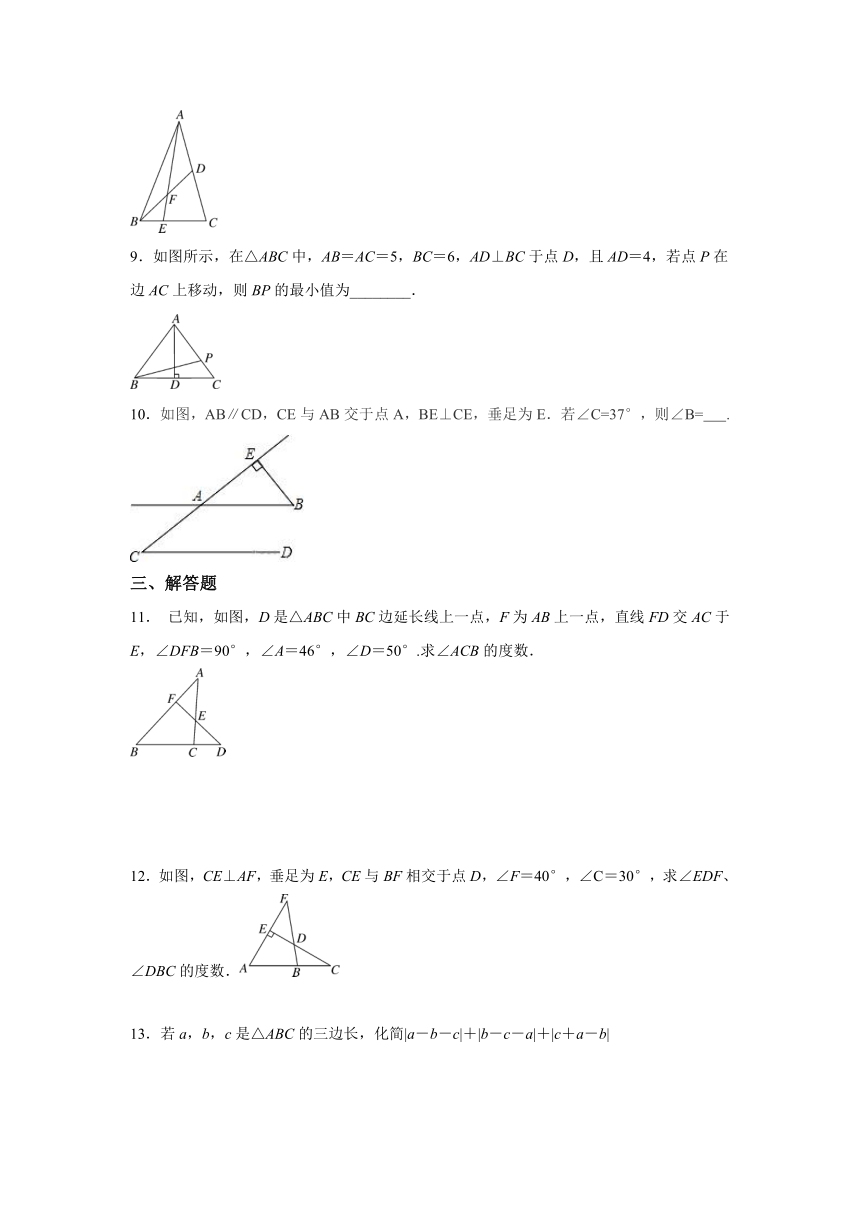
9.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
10.如图,AB∥CD,CE与AB交于点A,BE⊥CE,垂足为E.若∠C=37°,则∠B=
.
三、解答题
11.
已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.
12.如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
13.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|
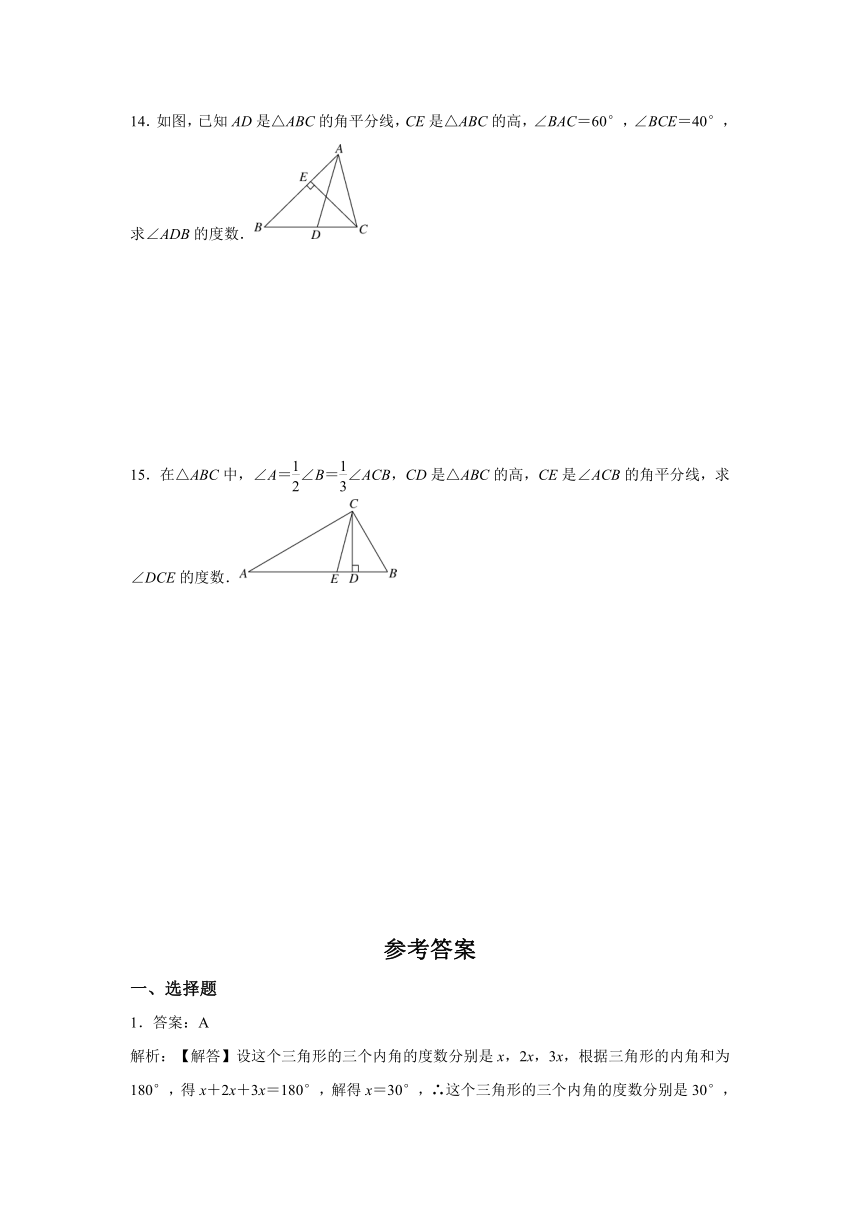
14.如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
15.在△ABC中,∠A=∠B=∠ACB,CD是△ABC的高,CE是∠ACB的角平分线,求∠DCE的度数.
参考答案
一、选择题
1.答案:A
解析:【解答】设这个三角形的三个内角的度数分别是x,2x,3x,根据三角形的内角和为180°,得x+2x+3x=180°,解得x=30°,∴这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.故选A.【分析】判断三角形的形状,可从角的大小来判断,根据三角形的内角和及角之间的关系列出相关方程式求解即可.
2.答案:B
解析:【解答】选项A中2+3=5,不能组成三角形,故此选项错误;选项B中5+6>10,能组成三角形,故此选项正确;选项C中1+1<3,不能组成三角形,故此选项错误;选项D中3+4<9,不能组成三角形,故此选项错误.故选B.
【分析】判定三条线段能否组成三角形,只要判定两条较短的线段长度之和大于第三条线段的长度即可.
3.答案:A
解析:【解答】∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.故选A.
【分析】判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
4.答案:D
解析:【解答】从三角形的顶点向它的对边引垂线,顶点和垂足间的线段叫做三角形的高.过点C作边AB的垂线段,即作AB边上的高CD,所以作法正确的是D.故选D.
【分析】三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
5.答案:B
解析:【解答】∵两个锐角和是90°,
∴一个直角三角形两个锐角的差为22°,
设一个锐角为x,则另一个锐角为90°-x,
得:90°-x-x=22°,
得:x=34°.
故选B.
【分析】根据直角三角形中两锐角和为90°,再根据两个锐角之差为22°,设其中一个角为x,则另一个为90°-x,即可求出最小的锐角度数.
6.答案:D
解析:【解答】∵直角三角形中,一个锐角等于60°,
∴另一个锐角的度数=90°-60°=30°.
故选:D.
【分析】根据直角三角形两锐角互余列式计算即可得解.
二、填空题
7.答案:7cm
解析:【解答】∵直角三角形中,一个锐角等于60°,
∴另一个锐角的度数=90°-60°=30°.
故选:D.
【分析】通过本题要理解三角形的中线的定义,解决问题的关键是将△ABD与△ADC的周长之差转化为边长的差.
8.答案:2
解析:【解答】∵点D是AC的中点,∴AD=AC.∵S△ABC=12,∴S△ABD=S△ABC=×12=6.∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
【分析】三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比,进行分析可得答案.
9.答案:
解析:【解答】根据“垂线段最短”,当BP⊥AC时,BP有最小值.由△ABC的面积公式可知AD·BC=BP·AC,解得BP=.
【分析】解答此题可利用面积相等作桥梁(但不求面积)求三角形的高,这种解题方法通常称为“面积法”.
10.答案:53°
解析:【解答】∵AB∥CD,
∴∠C=∠BAE=37°,
∵BE⊥CE,
∴∠BAE=90°,
∴∠B=90°-∠BAE=90°-37°=53°.
【分析】先根据平行线的性质得出∠BAE的度数,再由直角三角形的性质即可得出结论.
三、解答题
11.答案:94°.
解析:【解答】在△DFB中,∵∠DFB=90°,∠D=50°,∠DFB+∠D+∠B=180°,∴∠B=40°.在△ABC中,∵∠A=46°,∠B=40°,∴∠ACB=180°-∠A-∠B=94°.【分析】在△DFB中,根据三角形内角和定理,求得∠B的度数,再在△ABC中求∠ACB的度数即可.
12.答案:50°、100°.
解析:【解答】∵CE⊥AF,∴∠DEF=90°,∴∠EDF=90°-∠F=90°-40°=50°.由三角形的内角和定理得∠C+∠DBC+∠CDB=∠F+∠DEF+∠EDF,又∵∠CDB=∠EDF,∴30°+∠DBC=40°+90°,∴∠DBC=100°.
【分析】根据直角三角形两锐角互余列式计算即可求出∠EDF,再根据三角形的内角和定理求出∠C+∠DBC=∠F+∠DEF,然后求解即可.
13.答案:见解答过程.
解析:【解答】根据三角形的三边关系,两边之和大于第三边,得a-b-c<0,b-c-a<0,c+a-b>0.∴|a-b-c|+|b-c-a|+|c+a-b|=b+c-a+c+a-b+c+a-b=3c+a-b.
【分析】根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负,然后去绝对值符号进行计算.
14.答案:100°.
解析:【解答】∵AD是△ABC的角平分线,∠BAC=60°,∴∠DAC=∠BAD=30°.∵CE是△ABC的高,∠BCE=40°,∴∠B=50°,∴∠ADB=180°-∠B-∠BAD=180°-30°-50°=100°.
【分析】
根据AD是△ABC的角平分线,∠BAC=60°,得出∠BAD=30°.再利用CE是△ABC的高,∠BCE=40°,得出∠B的度数,进而得出∠ADB的度数.
15.答案:15°.
解析:【解答】∵∠A=∠B=∠ACB,设∠A=x,∴∠B=2x,∠ACB=3x.∵∠A+∠B+∠ACB=180°,∴x+2x+3x=180°,解得x=30°,∴∠A=30°,∠ACB=90°.∵CD是△ABC的高,∴∠ADC=90°,∴∠ACD=90°-30°=60°.∵CE是∠ACB的角平分线,∴∠ACE=×90°=45°,∴∠DCE=∠ACD-∠ACE=60°-45°=15°
【分析】根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,然后根据直角三角形两锐角互余求出∠ACD,最后根据角平分线的定义求出∠ACE即可.
一、选择题
1.一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法判定
2.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm
B.5cm,6cm,10cm
C.1cm,1cm,3cm
D.3cm,4cm,9cm
3.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
4.作△ABC的边AB上的高,下列作法中,正确的是( )
5.若直角三角形中的两个锐角之差为22°,则较小的一个锐角的度数是(
)
A.24°
B.34°
C.44°
D.46°
6.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是(
)
A.120°
B.90°
C.60°
D.30°
二、填空题
7.在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
8.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
9.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
10.如图,AB∥CD,CE与AB交于点A,BE⊥CE,垂足为E.若∠C=37°,则∠B=
.
三、解答题
11.
已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.
12.如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
13.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|
14.如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
15.在△ABC中,∠A=∠B=∠ACB,CD是△ABC的高,CE是∠ACB的角平分线,求∠DCE的度数.
参考答案
一、选择题
1.答案:A
解析:【解答】设这个三角形的三个内角的度数分别是x,2x,3x,根据三角形的内角和为180°,得x+2x+3x=180°,解得x=30°,∴这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.故选A.【分析】判断三角形的形状,可从角的大小来判断,根据三角形的内角和及角之间的关系列出相关方程式求解即可.
2.答案:B
解析:【解答】选项A中2+3=5,不能组成三角形,故此选项错误;选项B中5+6>10,能组成三角形,故此选项正确;选项C中1+1<3,不能组成三角形,故此选项错误;选项D中3+4<9,不能组成三角形,故此选项错误.故选B.
【分析】判定三条线段能否组成三角形,只要判定两条较短的线段长度之和大于第三条线段的长度即可.
3.答案:A
解析:【解答】∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.故选A.
【分析】判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
4.答案:D
解析:【解答】从三角形的顶点向它的对边引垂线,顶点和垂足间的线段叫做三角形的高.过点C作边AB的垂线段,即作AB边上的高CD,所以作法正确的是D.故选D.
【分析】三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
5.答案:B
解析:【解答】∵两个锐角和是90°,
∴一个直角三角形两个锐角的差为22°,
设一个锐角为x,则另一个锐角为90°-x,
得:90°-x-x=22°,
得:x=34°.
故选B.
【分析】根据直角三角形中两锐角和为90°,再根据两个锐角之差为22°,设其中一个角为x,则另一个为90°-x,即可求出最小的锐角度数.
6.答案:D
解析:【解答】∵直角三角形中,一个锐角等于60°,
∴另一个锐角的度数=90°-60°=30°.
故选:D.
【分析】根据直角三角形两锐角互余列式计算即可得解.
二、填空题
7.答案:7cm
解析:【解答】∵直角三角形中,一个锐角等于60°,
∴另一个锐角的度数=90°-60°=30°.
故选:D.
【分析】通过本题要理解三角形的中线的定义,解决问题的关键是将△ABD与△ADC的周长之差转化为边长的差.
8.答案:2
解析:【解答】∵点D是AC的中点,∴AD=AC.∵S△ABC=12,∴S△ABD=S△ABC=×12=6.∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
【分析】三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比,进行分析可得答案.
9.答案:
解析:【解答】根据“垂线段最短”,当BP⊥AC时,BP有最小值.由△ABC的面积公式可知AD·BC=BP·AC,解得BP=.
【分析】解答此题可利用面积相等作桥梁(但不求面积)求三角形的高,这种解题方法通常称为“面积法”.
10.答案:53°
解析:【解答】∵AB∥CD,
∴∠C=∠BAE=37°,
∵BE⊥CE,
∴∠BAE=90°,
∴∠B=90°-∠BAE=90°-37°=53°.
【分析】先根据平行线的性质得出∠BAE的度数,再由直角三角形的性质即可得出结论.
三、解答题
11.答案:94°.
解析:【解答】在△DFB中,∵∠DFB=90°,∠D=50°,∠DFB+∠D+∠B=180°,∴∠B=40°.在△ABC中,∵∠A=46°,∠B=40°,∴∠ACB=180°-∠A-∠B=94°.【分析】在△DFB中,根据三角形内角和定理,求得∠B的度数,再在△ABC中求∠ACB的度数即可.
12.答案:50°、100°.
解析:【解答】∵CE⊥AF,∴∠DEF=90°,∴∠EDF=90°-∠F=90°-40°=50°.由三角形的内角和定理得∠C+∠DBC+∠CDB=∠F+∠DEF+∠EDF,又∵∠CDB=∠EDF,∴30°+∠DBC=40°+90°,∴∠DBC=100°.
【分析】根据直角三角形两锐角互余列式计算即可求出∠EDF,再根据三角形的内角和定理求出∠C+∠DBC=∠F+∠DEF,然后求解即可.
13.答案:见解答过程.
解析:【解答】根据三角形的三边关系,两边之和大于第三边,得a-b-c<0,b-c-a<0,c+a-b>0.∴|a-b-c|+|b-c-a|+|c+a-b|=b+c-a+c+a-b+c+a-b=3c+a-b.
【分析】根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负,然后去绝对值符号进行计算.
14.答案:100°.
解析:【解答】∵AD是△ABC的角平分线,∠BAC=60°,∴∠DAC=∠BAD=30°.∵CE是△ABC的高,∠BCE=40°,∴∠B=50°,∴∠ADB=180°-∠B-∠BAD=180°-30°-50°=100°.
【分析】
根据AD是△ABC的角平分线,∠BAC=60°,得出∠BAD=30°.再利用CE是△ABC的高,∠BCE=40°,得出∠B的度数,进而得出∠ADB的度数.
15.答案:15°.
解析:【解答】∵∠A=∠B=∠ACB,设∠A=x,∴∠B=2x,∠ACB=3x.∵∠A+∠B+∠ACB=180°,∴x+2x+3x=180°,解得x=30°,∴∠A=30°,∠ACB=90°.∵CD是△ABC的高,∴∠ADC=90°,∴∠ACD=90°-30°=60°.∵CE是∠ACB的角平分线,∴∠ACE=×90°=45°,∴∠DCE=∠ACD-∠ACE=60°-45°=15°
【分析】根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,然后根据直角三角形两锐角互余求出∠ACD,最后根据角平分线的定义求出∠ACE即可.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
