2017年中考数学二轮专题复习讲义第13讲动态运动问题
文档属性
| 名称 | 2017年中考数学二轮专题复习讲义第13讲动态运动问题 |  | |
| 格式 | zip | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-02 09:35:19 | ||
图片预览




文档简介
2017年中考数学二轮专题复习讲义(13)动态运动问题
【专题点拨】
动态问题就是研究在几何图形的运动中伴随着一定的图形位置、数量关系的“变”与“不变”性.就其运动对象而言,有“点动” “线动”和“面动”;就其运动形式而言,有“移动”“滚动”“旋转”和“翻折”等.
【解题策略】
动态几何问题常集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活多变,动中有静,动静结合,能够在运动变化过程中发展学生思维和空间想象能力,是中考热点,常在中考中以压轴题的形式出现.
【典例解析】
类型一:一点动型问题
例题1:(2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
【考点】动点问题的函数图象.
【分析】△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
变式训练1:
(2016·青海西宁·3分)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )【来源:21·世纪·教育·网】
A. B. C.D.
类型二: 两点动型问题
例题2:(2016·四川内江)如图12所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是______.
【考点】勾股定理,对称问题。
【解答】作点C关于y轴的对称点C1(-1,0),点C关于x轴的对称点C2,连接C1C2交OA于点E,交AB于点D,则此时△CDE的周长最小,且最小值等于C1C2的长.
∵OA=OB=7,∴CB=6,∠ABC=45°.
∵AB垂直平分CC2,
∴∠CBC2=90°,C2的坐标为(7,6).
在△C1BC2中,C1C2===10.
即△CDE周长的最小值是10.
故答案为:10.
变式训练2:
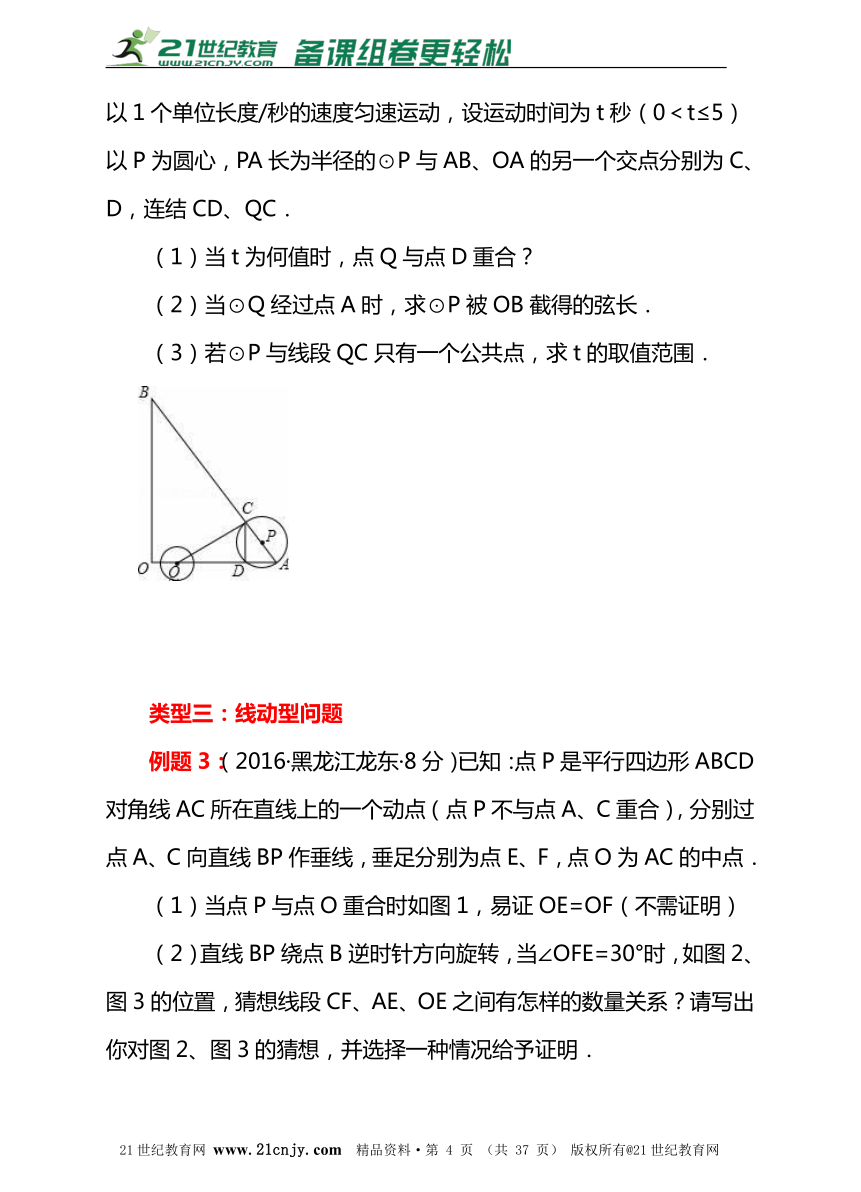
(2016·四川攀枝花)如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
类型三:线动型问题
例题3:(2016·黑龙江龙东·8分)已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
【考点】四边形综合题.
【分析】(1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.
【解答】解:(1)∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
,
∴△AOE≌△COF,
∴OE=OF.
(2)图2中的结论为:CF=OE+AE.
图3中的结论为:CF=OE﹣AE.
选图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
,
∴△EOA≌△GOC,
∴EO=GO,AE=CG,
在RT△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=GF,
∵OE=OF,
∴OE=FG,
∵CF=FG+CG,
∴CF=OE+AE.
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
,
∴△AOE≌△COG,
∴OE=OG,AE=CG,
在RT△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG﹣CG,
∴CF=OE﹣AE.
变式训练3:
(2015湖南邵阳第9题3分)如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
A. B.
C. D.
【解析】
【解答】
类型四:图动型问题
例题4:(2016江苏淮安,18,3分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 1.2 .www-2-1-cnjy-com
【考点】翻折变换(折叠问题).
【分析】如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小,利用△AFM∽△ABC,得到=求出FM即可解决问题.
【解答】解:如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴=,
∵CF=2,AC=6,BC=8,
∴AF=4,AB==10,
∴=,
∴FM=3.2,
∵PF=CF=2,
∴PM=1.2
∴点P到边AB距离的最小值是1.2.
故答案为1.2.
【点评】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P位置,属于中考常考题型.【来源:21cnj*y.co*m】
变式训练4:
(2016·广东梅州)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为______________.【版权所有:21教育】
【能力检测】
1. (2016.山东省临沂市,3分)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:21教育名师原创作品
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
2. (2015年浙江舟山4分)如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1. 点M从A开始沿⊙P按逆时针方向转动,射线AM交轴于点N(,0). 设点M转过的路程为(). 随着点M的转动,当从变化到时,点N相应移动的路径长为 21*cnjy*com
3. (2015?聊城)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
4. 如图1,在Rt△ABC中,∠ACB=90°,AC=15cm,BC=20cm,点D从点B出发沿BC边向点C运动,同时点E从点A出发沿AC边向点C运动,速度均为1cm/s,当一个点到达点C时,另一点也停止运动,连接DE,设点D的运动时间为t(单位:s,0≤t<15),△CDE的面积为S(单位:cm2)21世纪教育网版权所有
(1)在点D、E运动过程中,DC﹣EC= 5 cm,并求出S与t的函数关系式;
(2)点D运动到什么位置时,S等于△ABC面积的一半?
(3)如图2,在点D、E运动的同时,将线段DE绕点E逆时针旋转45°,得到线段EP,过点D作DF⊥EP,垂足为F,连接CF,在DC上截取GC=5cm,连接FG,在点D、E运动过程中,线段CF的长是一个定值,求出其值;
(4)点D、E及EP按照(3)中的方式运动到某个时刻停止,仍过点D作DF⊥EP,垂足为F,如图3,令点Q在DE的右侧运动(点Q不与A、B重合),且DQ⊥EQ,连接QF,若DQ=m,EQ=n(m>0,n>0且m≠n),直接写出QF的长(用含m,n的式子表示)
5. (2016·四川攀枝花)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【参考答案】
变式训练1:
(2016·青海西宁·3分)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. B. C.D.
【考点】动点问题的函数图象.
【分析】根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.
【解答】解:作AD∥x轴,作CD⊥AD于点D,若右图所示,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
∵AD∥x轴,
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
,
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选:A.
变式训练2:
(2016·四川攀枝花)如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
【考点】圆的综合题.
【分析】(1)由题意知CD⊥OA,所以△ACD∽△ABO,利用对应边的比求出AD的长度,若Q与D重合时,则,AD+OQ=OA,列出方程即可求出t的值;
(2)由于0<t≤5,当Q经过A点时,OQ=4,此时用时为4s,过点P作PE⊥OB于点E,利用垂径定理即可求出⊙P被OB截得的弦长;
(3)若⊙P与线段QC只有一个公共点,分以下两种情况,①当QC与⊙P相切时,计算出此时的时间;②当Q与D重合时,计算出此时的时间;由以上两种情况即可得出t的取值范围.
【解答】解:(1)∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴,
∴AD=,
当Q与D重合时,
AD+OQ=OA,
∴+t=6,
∴t=;
(2)当⊙Q经过A点时,如图1,
OQ=OA﹣QA=4,
∴t==4s,
∴PA=4,
∴BP=AB﹣PA=6,
过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,
连接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴,
∴PE=,
∴由勾股定理可求得:EF=,
由垂径定理可求知:FG=2EF=;
(3)当QC与⊙P相切时,如图2,
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴,
∴,
∴t=,
∴当0<t≤时,⊙P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=,
∴当<t≤5时,⊙P与QC只有一个交点,
综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤或<t≤5.
【点评】本题考查圆的综合问题,涉及圆的切线判定,圆周角定理,相似三角形的判定与性质,学生需要根据题意画出相应的图形来分析,并且能综合运用所学知识进行解答.2-1-c-n-j-y
变式训练3:
(2015湖南邵阳第9题3分)如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
A. B. C. D.
【解析】动点问题的函数图象.数形结合,作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,根据等腰三角形的性质得∠B=∠C,BD=CD=m,当点F从点B运动到D时,如图1,利用正切定义即可得到y=tanB?t(0≤t≤m);当点F从点D运动到C时,如图2,利用正切定义可得y=tanC?CF=﹣tanB?t+2mtanB(m≤t≤2m),即y与t的函数关系为两个一次函数关系式,于是可对四个选项进行判断.
解答:作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,
∵△ABC为等腰三角形,
∴∠B=∠C,BD=CD,
当点F从点B运动到D时,如图1,
在Rt△BEF中,∵tanB=,
∴y=tanB?t(0≤t≤m);
当点F从点D运动到C时,如图2,
在Rt△CEF中,∵tanC=,
∴y=tanC?CF
=tanC?(2m﹣t)
=﹣tanB?t+2mtanB(m≤t≤2m).
故选B.
点评:本题考查了动点问题的函数图象:利用三角函数关系得到两变量的函数关系,再利用函数关系式画出对应的函数图象.注意自变量的取值范围.21*cnjy*com
变式训练4:
(2016·广东梅州)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为______________.
【答案】:(6048,2)
【考点】:坐标与图形的变换—旋转,规律探索,勾股定理。
【解析】:OA=,OB=2,由勾股定理,得:AB=,所以,OC2=2++=6,
所以,B2(6,2),同理可得:B4(12,2),B6(18,2),…
所以,B2016的横坐标为:10086=6048,所以,B2016(6048,2)
【能力检测】
1. (2016.山东省临沂市,3分)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:【出处:21教育名师】
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【考点】旋转的性质;等边三角形的性质;菱形的判定.
【分析】根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.
【解答】解:∵将等边△ABC绕点C顺时针旋转120°得到△EDC,
∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,
∴∠ACD=120°﹣60°=60°,
∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE,
∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴BD⊥AC,∴①②③都正确,
故选D.
【点评】本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.21·cn·jy·com
2. (2015年浙江舟山4分)如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1. 点M从A开始沿⊙P按逆时针方向转动,射线AM交轴于点N(,0). 设点M转过的路程为(). 随着点M的转动,当从变化到时,点N相应移动的路径长为
【答案】.
【解答】∵以AP为半径的⊙P周长为1,
∴当从变化到时,点M转动的圆心角为120°,即圆周角为60°.
∴根据对称性,当点M转动的圆心角为120°时,点N相应移动的路径起点和终点关于轴对称.
∴此时构成等边三角形,且.
∵点A(0,1),即OA=1,∴.
∴当从变化到时,点N相应移动的路径长为
3. (2015?聊城)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
11. 解:(1)根据题意得:MA=x,ON=1.25x,
在Rt△OAB中,由勾股定理得:OB===5,
作NP⊥OA于P,如图1所示:
则NP∥AB,
∴△OPN∽△OAB,
∴,
即,
解得:OP=x,PN=,
∴点N的坐标是(x,);
(2)在△OMN中,OM=4﹣x,OM边上的高PN=,
∴S=OM?PN=(4﹣x)?=﹣x2+x,
∴S与x之间的函数表达式为S=﹣x2+x(0<x<4),
配方得:S=﹣(x﹣2)2+,
∵﹣<0,
∴S有最大值,
当x=2时,S有最大值,最大值是;
(3)存在某一时刻,使△OMN是直角三角形,理由如下:
分两种情况:①若∠OMN=90°,如图2所示:
则MN∥AB,
此时OM=4﹣x,ON=1.25x,
∵MN∥AB,
∴△OMN∽△OAB,
∴,
即,
解得:x=2;
②若∠ONM=90°,如图3所示:
则∠ONM=∠OAB,
此时OM=4﹣x,ON=1.25x,
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴,
即,
解得:x=;
综上所述:x的值是2秒或秒.
4. 如图1,在Rt△ABC中,∠ACB=90°,AC=15cm,BC=20cm,点D从点B出发沿BC边向点C运动,同时点E从点A出发沿AC边向点C运动,速度均为1cm/s,当一个点到达点C时,另一点也停止运动,连接DE,设点D的运动时间为t(单位:s,0≤t<15),△CDE的面积为S(单位:cm2)21教育网
(1)在点D、E运动过程中,DC﹣EC= 5 cm,并求出S与t的函数关系式;
(2)点D运动到什么位置时,S等于△ABC面积的一半?
(3)如图2,在点D、E运动的同时,将线段DE绕点E逆时针旋转45°,得到线段EP,过点D作DF⊥EP,垂足为F,连接CF,在DC上截取GC=5cm,连接FG,在点D、E运动过程中,线段CF的长是一个定值,求出其值;21cnjy.com
(4)点D、E及EP按照(3)中的方式运动到某个时刻停止,仍过点D作DF⊥EP,垂足为F,如图3,令点Q在DE的右侧运动(点Q不与A、B重合),且DQ⊥EQ,连接QF,若DQ=m,EQ=n(m>0,n>0且m≠n),直接写出QF的长(用含m,n的式子表示)
【解析】(1)由题意知AE=BD=t,所以EC=15﹣t,DC=20﹣t,代入DC﹣EC中即可求出它的值,另外S=EC?DC,分别将DC和EC代入即可求出S与t的函数关系式;www.21-cn-jy.com
(2)容易求出△ABC的面积,令(1)的函数解析式中的S=75,即可求出t的值,要注意t的范围;
(3)延长AC至H使得,CH=GC=5,连接HF,利用条件易证△HEF≌△CDF,所以HF=CF,∠FHE=∠FCD,即可证明△HFC是等腰直角三角形,从而可知CF=CH;2·1·c·n·j·y
(4)延长QD至点G,使得DG=QE,连接GF,易证△GDF≌△QEF,所以GF=QF,∠GFD=∠QFE,从而可证明△GFQ是等腰直角三角形,所以FQ=QG=(DG+DQ)=(m+n).21·世纪*教育网
【解答】解:(1)由题意知:AE=BD=t,
∴EC=15﹣t,DC=20﹣t,
∴DC﹣EC=(20﹣t)﹣(15﹣t)=5,
∴S=EC?DC
=(15﹣t)(20﹣t)
=﹣+150
故答案为:5;
(2)△ABC的面积为×20×15=150,
当S=×150时,
∴﹣+150=75,
解得:t=5或t=30,
∵0≤t<15,
∴t=5,
∴BD=t=5,
∴点D运动到BD处时,S等于△ABC面积的一半;
(3)延长AC至H使得,CH=GC=5,
连接HF,如图2,
由(1)可知,DC﹣EC=5,
即DC﹣EC=CH,
∴DC=EC+CH=EH,
∵DF⊥EF,∠DEF=45°,
∴△DFE是等腰直角三角形,
∴DF=EF,
∵∠DFE=∠DCE=90°,
∴F、C、E、D四点共圆,
∴∠FDC=∠FEH,
在△HEF与△CDF中,
,
∴△HEF≌△CDF(SAS),
∴HF=CF,∠FHE=∠FCD,
∵HF=CF,
∴∠FHE=∠FCH,
∴∠FCH=∠FCD,
∵∠HCB=90°,
∴∠FCH=∠FCD=45°,
∴△HFC是等腰直角三角形,
∴CF=CH=;
(4)延长QD至点G,使得DG=QE,
连接GF,
∵∠DFE=∠DQE=90°,
∴∠FDQ+∠FEQ=180°,
∵∠GDF+∠FDQ=180°,
∴∠GDF=∠QEF,
由(3)可知:△DFE是等腰直角三角形,
∴DF=EF,
在△GDF与△QEF中,
∴△GDF≌△QEF(SAS),
∴GF=QF,∠GFD=∠QFE,
∴∠DFQ+∠QFE=∠DFQ+∠GFD,
∴∠DFE=∠GFQ=90°,
∴△GFQ是等腰直角三角形,
∴FQ=QG=(DG+DQ)=(m+n).
5. (2016·四川攀枝花)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;
(2)连接BC,则△ABC的面积是不变的,过P作PM∥y轴,交BC于点M,设出P点坐标,可表示出PM的长,可知当PM取最大值时△PBC的面积最大,利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积;
(3)设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,则可证得△AOC≌△NOB,可求得ON的长,可求出N点坐标,利用B、N两的点坐标可求得直线m的解析式.
【解答】解:
(1)把B、C两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H,
在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∴AB=3﹣(﹣1)=4,且OC=3,
∴S△ABC=AB?OC=×4×3=6,
∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),
∵P点在第四限,
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△PBC=PM?OH+PM?HB=PM?(OH+HB)=PM?OB=PM,
∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,
∵PM=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,PMmax=,则S△PBC=×=,
此时P点坐标为(,﹣),S四边形ABPC=S△ABC+S△PBC=6+=,
即当P点坐标为(,﹣)时,四边形ABPC的面积最大,最大面积为;
(3)如图2,设直线m交y轴于点N,交直线l于点G,
则∠AGP=∠GNC+∠GCN,
当△AGB和△NGC相似时,必有∠AGB=∠CGB,
又∠AGB+∠CGB=180°,
∴∠AGB=∠CGB=90°,
∴∠ACO=∠OBN,
在Rt△AON和Rt△NOB中
∴Rt△AON≌Rt△NOB(ASA),
∴ON=OA=1,
∴N点坐标为(0,﹣1),
设直线m解析式为y=kx+d,把B、N两点坐标代入可得,解得,
∴直线m解析式为y=x﹣1,
即存在满足条件的直线m,其解析式为y=x﹣1.
【点评】本题为二次函数的综合应用,涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等.在(2)中确定出PM的值最时四边形ABPC的面积最大是解题的关键,在(3)中确定出满足条件的直线m的位置是解题的关键.本题考查知识点较多,综合性较强,特别是第(2)问和第(3)问难度较大.
【专题点拨】
动态问题就是研究在几何图形的运动中伴随着一定的图形位置、数量关系的“变”与“不变”性.就其运动对象而言,有“点动” “线动”和“面动”;就其运动形式而言,有“移动”“滚动”“旋转”和“翻折”等.
【解题策略】
动态几何问题常集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活多变,动中有静,动静结合,能够在运动变化过程中发展学生思维和空间想象能力,是中考热点,常在中考中以压轴题的形式出现.
【典例解析】
类型一:一点动型问题
例题1:(2016·湖北荆门·3分)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
【考点】动点问题的函数图象.
【分析】△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
变式训练1:
(2016·青海西宁·3分)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )【来源:21·世纪·教育·网】
A. B. C.D.
类型二: 两点动型问题
例题2:(2016·四川内江)如图12所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是______.
【考点】勾股定理,对称问题。
【解答】作点C关于y轴的对称点C1(-1,0),点C关于x轴的对称点C2,连接C1C2交OA于点E,交AB于点D,则此时△CDE的周长最小,且最小值等于C1C2的长.
∵OA=OB=7,∴CB=6,∠ABC=45°.
∵AB垂直平分CC2,
∴∠CBC2=90°,C2的坐标为(7,6).
在△C1BC2中,C1C2===10.
即△CDE周长的最小值是10.
故答案为:10.
变式训练2:
(2016·四川攀枝花)如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
类型三:线动型问题
例题3:(2016·黑龙江龙东·8分)已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
【考点】四边形综合题.
【分析】(1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.
【解答】解:(1)∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
,
∴△AOE≌△COF,
∴OE=OF.
(2)图2中的结论为:CF=OE+AE.
图3中的结论为:CF=OE﹣AE.
选图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
,
∴△EOA≌△GOC,
∴EO=GO,AE=CG,
在RT△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=GF,
∵OE=OF,
∴OE=FG,
∵CF=FG+CG,
∴CF=OE+AE.
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
,
∴△AOE≌△COG,
∴OE=OG,AE=CG,
在RT△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG﹣CG,
∴CF=OE﹣AE.
变式训练3:
(2015湖南邵阳第9题3分)如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
A. B.
C. D.
【解析】
【解答】
类型四:图动型问题
例题4:(2016江苏淮安,18,3分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 1.2 .www-2-1-cnjy-com
【考点】翻折变换(折叠问题).
【分析】如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小,利用△AFM∽△ABC,得到=求出FM即可解决问题.
【解答】解:如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴=,
∵CF=2,AC=6,BC=8,
∴AF=4,AB==10,
∴=,
∴FM=3.2,
∵PF=CF=2,
∴PM=1.2
∴点P到边AB距离的最小值是1.2.
故答案为1.2.
【点评】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P位置,属于中考常考题型.【来源:21cnj*y.co*m】
变式训练4:
(2016·广东梅州)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为______________.【版权所有:21教育】
【能力检测】
1. (2016.山东省临沂市,3分)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:21教育名师原创作品
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
2. (2015年浙江舟山4分)如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1. 点M从A开始沿⊙P按逆时针方向转动,射线AM交轴于点N(,0). 设点M转过的路程为(). 随着点M的转动,当从变化到时,点N相应移动的路径长为 21*cnjy*com
3. (2015?聊城)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
4. 如图1,在Rt△ABC中,∠ACB=90°,AC=15cm,BC=20cm,点D从点B出发沿BC边向点C运动,同时点E从点A出发沿AC边向点C运动,速度均为1cm/s,当一个点到达点C时,另一点也停止运动,连接DE,设点D的运动时间为t(单位:s,0≤t<15),△CDE的面积为S(单位:cm2)21世纪教育网版权所有
(1)在点D、E运动过程中,DC﹣EC= 5 cm,并求出S与t的函数关系式;
(2)点D运动到什么位置时,S等于△ABC面积的一半?
(3)如图2,在点D、E运动的同时,将线段DE绕点E逆时针旋转45°,得到线段EP,过点D作DF⊥EP,垂足为F,连接CF,在DC上截取GC=5cm,连接FG,在点D、E运动过程中,线段CF的长是一个定值,求出其值;
(4)点D、E及EP按照(3)中的方式运动到某个时刻停止,仍过点D作DF⊥EP,垂足为F,如图3,令点Q在DE的右侧运动(点Q不与A、B重合),且DQ⊥EQ,连接QF,若DQ=m,EQ=n(m>0,n>0且m≠n),直接写出QF的长(用含m,n的式子表示)
5. (2016·四川攀枝花)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【参考答案】
变式训练1:
(2016·青海西宁·3分)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. B. C.D.
【考点】动点问题的函数图象.
【分析】根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.
【解答】解:作AD∥x轴,作CD⊥AD于点D,若右图所示,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
∵AD∥x轴,
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
,
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选:A.
变式训练2:
(2016·四川攀枝花)如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
【考点】圆的综合题.
【分析】(1)由题意知CD⊥OA,所以△ACD∽△ABO,利用对应边的比求出AD的长度,若Q与D重合时,则,AD+OQ=OA,列出方程即可求出t的值;
(2)由于0<t≤5,当Q经过A点时,OQ=4,此时用时为4s,过点P作PE⊥OB于点E,利用垂径定理即可求出⊙P被OB截得的弦长;
(3)若⊙P与线段QC只有一个公共点,分以下两种情况,①当QC与⊙P相切时,计算出此时的时间;②当Q与D重合时,计算出此时的时间;由以上两种情况即可得出t的取值范围.
【解答】解:(1)∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴,
∴AD=,
当Q与D重合时,
AD+OQ=OA,
∴+t=6,
∴t=;
(2)当⊙Q经过A点时,如图1,
OQ=OA﹣QA=4,
∴t==4s,
∴PA=4,
∴BP=AB﹣PA=6,
过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,
连接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴,
∴PE=,
∴由勾股定理可求得:EF=,
由垂径定理可求知:FG=2EF=;
(3)当QC与⊙P相切时,如图2,
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴,
∴,
∴t=,
∴当0<t≤时,⊙P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=,
∴当<t≤5时,⊙P与QC只有一个交点,
综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤或<t≤5.
【点评】本题考查圆的综合问题,涉及圆的切线判定,圆周角定理,相似三角形的判定与性质,学生需要根据题意画出相应的图形来分析,并且能综合运用所学知识进行解答.2-1-c-n-j-y
变式训练3:
(2015湖南邵阳第9题3分)如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
A. B. C. D.
【解析】动点问题的函数图象.数形结合,作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,根据等腰三角形的性质得∠B=∠C,BD=CD=m,当点F从点B运动到D时,如图1,利用正切定义即可得到y=tanB?t(0≤t≤m);当点F从点D运动到C时,如图2,利用正切定义可得y=tanC?CF=﹣tanB?t+2mtanB(m≤t≤2m),即y与t的函数关系为两个一次函数关系式,于是可对四个选项进行判断.
解答:作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,
∵△ABC为等腰三角形,
∴∠B=∠C,BD=CD,
当点F从点B运动到D时,如图1,
在Rt△BEF中,∵tanB=,
∴y=tanB?t(0≤t≤m);
当点F从点D运动到C时,如图2,
在Rt△CEF中,∵tanC=,
∴y=tanC?CF
=tanC?(2m﹣t)
=﹣tanB?t+2mtanB(m≤t≤2m).
故选B.
点评:本题考查了动点问题的函数图象:利用三角函数关系得到两变量的函数关系,再利用函数关系式画出对应的函数图象.注意自变量的取值范围.21*cnjy*com
变式训练4:
(2016·广东梅州)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为______________.
【答案】:(6048,2)
【考点】:坐标与图形的变换—旋转,规律探索,勾股定理。
【解析】:OA=,OB=2,由勾股定理,得:AB=,所以,OC2=2++=6,
所以,B2(6,2),同理可得:B4(12,2),B6(18,2),…
所以,B2016的横坐标为:10086=6048,所以,B2016(6048,2)
【能力检测】
1. (2016.山东省临沂市,3分)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:【出处:21教育名师】
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【考点】旋转的性质;等边三角形的性质;菱形的判定.
【分析】根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.
【解答】解:∵将等边△ABC绕点C顺时针旋转120°得到△EDC,
∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,
∴∠ACD=120°﹣60°=60°,
∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE,
∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴BD⊥AC,∴①②③都正确,
故选D.
【点评】本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.21·cn·jy·com
2. (2015年浙江舟山4分)如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1. 点M从A开始沿⊙P按逆时针方向转动,射线AM交轴于点N(,0). 设点M转过的路程为(). 随着点M的转动,当从变化到时,点N相应移动的路径长为
【答案】.
【解答】∵以AP为半径的⊙P周长为1,
∴当从变化到时,点M转动的圆心角为120°,即圆周角为60°.
∴根据对称性,当点M转动的圆心角为120°时,点N相应移动的路径起点和终点关于轴对称.
∴此时构成等边三角形,且.
∵点A(0,1),即OA=1,∴.
∴当从变化到时,点N相应移动的路径长为
3. (2015?聊城)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
11. 解:(1)根据题意得:MA=x,ON=1.25x,
在Rt△OAB中,由勾股定理得:OB===5,
作NP⊥OA于P,如图1所示:
则NP∥AB,
∴△OPN∽△OAB,
∴,
即,
解得:OP=x,PN=,
∴点N的坐标是(x,);
(2)在△OMN中,OM=4﹣x,OM边上的高PN=,
∴S=OM?PN=(4﹣x)?=﹣x2+x,
∴S与x之间的函数表达式为S=﹣x2+x(0<x<4),
配方得:S=﹣(x﹣2)2+,
∵﹣<0,
∴S有最大值,
当x=2时,S有最大值,最大值是;
(3)存在某一时刻,使△OMN是直角三角形,理由如下:
分两种情况:①若∠OMN=90°,如图2所示:
则MN∥AB,
此时OM=4﹣x,ON=1.25x,
∵MN∥AB,
∴△OMN∽△OAB,
∴,
即,
解得:x=2;
②若∠ONM=90°,如图3所示:
则∠ONM=∠OAB,
此时OM=4﹣x,ON=1.25x,
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴,
即,
解得:x=;
综上所述:x的值是2秒或秒.
4. 如图1,在Rt△ABC中,∠ACB=90°,AC=15cm,BC=20cm,点D从点B出发沿BC边向点C运动,同时点E从点A出发沿AC边向点C运动,速度均为1cm/s,当一个点到达点C时,另一点也停止运动,连接DE,设点D的运动时间为t(单位:s,0≤t<15),△CDE的面积为S(单位:cm2)21教育网
(1)在点D、E运动过程中,DC﹣EC= 5 cm,并求出S与t的函数关系式;
(2)点D运动到什么位置时,S等于△ABC面积的一半?
(3)如图2,在点D、E运动的同时,将线段DE绕点E逆时针旋转45°,得到线段EP,过点D作DF⊥EP,垂足为F,连接CF,在DC上截取GC=5cm,连接FG,在点D、E运动过程中,线段CF的长是一个定值,求出其值;21cnjy.com
(4)点D、E及EP按照(3)中的方式运动到某个时刻停止,仍过点D作DF⊥EP,垂足为F,如图3,令点Q在DE的右侧运动(点Q不与A、B重合),且DQ⊥EQ,连接QF,若DQ=m,EQ=n(m>0,n>0且m≠n),直接写出QF的长(用含m,n的式子表示)
【解析】(1)由题意知AE=BD=t,所以EC=15﹣t,DC=20﹣t,代入DC﹣EC中即可求出它的值,另外S=EC?DC,分别将DC和EC代入即可求出S与t的函数关系式;www.21-cn-jy.com
(2)容易求出△ABC的面积,令(1)的函数解析式中的S=75,即可求出t的值,要注意t的范围;
(3)延长AC至H使得,CH=GC=5,连接HF,利用条件易证△HEF≌△CDF,所以HF=CF,∠FHE=∠FCD,即可证明△HFC是等腰直角三角形,从而可知CF=CH;2·1·c·n·j·y
(4)延长QD至点G,使得DG=QE,连接GF,易证△GDF≌△QEF,所以GF=QF,∠GFD=∠QFE,从而可证明△GFQ是等腰直角三角形,所以FQ=QG=(DG+DQ)=(m+n).21·世纪*教育网
【解答】解:(1)由题意知:AE=BD=t,
∴EC=15﹣t,DC=20﹣t,
∴DC﹣EC=(20﹣t)﹣(15﹣t)=5,
∴S=EC?DC
=(15﹣t)(20﹣t)
=﹣+150
故答案为:5;
(2)△ABC的面积为×20×15=150,
当S=×150时,
∴﹣+150=75,
解得:t=5或t=30,
∵0≤t<15,
∴t=5,
∴BD=t=5,
∴点D运动到BD处时,S等于△ABC面积的一半;
(3)延长AC至H使得,CH=GC=5,
连接HF,如图2,
由(1)可知,DC﹣EC=5,
即DC﹣EC=CH,
∴DC=EC+CH=EH,
∵DF⊥EF,∠DEF=45°,
∴△DFE是等腰直角三角形,
∴DF=EF,
∵∠DFE=∠DCE=90°,
∴F、C、E、D四点共圆,
∴∠FDC=∠FEH,
在△HEF与△CDF中,
,
∴△HEF≌△CDF(SAS),
∴HF=CF,∠FHE=∠FCD,
∵HF=CF,
∴∠FHE=∠FCH,
∴∠FCH=∠FCD,
∵∠HCB=90°,
∴∠FCH=∠FCD=45°,
∴△HFC是等腰直角三角形,
∴CF=CH=;
(4)延长QD至点G,使得DG=QE,
连接GF,
∵∠DFE=∠DQE=90°,
∴∠FDQ+∠FEQ=180°,
∵∠GDF+∠FDQ=180°,
∴∠GDF=∠QEF,
由(3)可知:△DFE是等腰直角三角形,
∴DF=EF,
在△GDF与△QEF中,
∴△GDF≌△QEF(SAS),
∴GF=QF,∠GFD=∠QFE,
∴∠DFQ+∠QFE=∠DFQ+∠GFD,
∴∠DFE=∠GFQ=90°,
∴△GFQ是等腰直角三角形,
∴FQ=QG=(DG+DQ)=(m+n).
5. (2016·四川攀枝花)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;
(2)连接BC,则△ABC的面积是不变的,过P作PM∥y轴,交BC于点M,设出P点坐标,可表示出PM的长,可知当PM取最大值时△PBC的面积最大,利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积;
(3)设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,则可证得△AOC≌△NOB,可求得ON的长,可求出N点坐标,利用B、N两的点坐标可求得直线m的解析式.
【解答】解:
(1)把B、C两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H,
在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∴AB=3﹣(﹣1)=4,且OC=3,
∴S△ABC=AB?OC=×4×3=6,
∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),
∵P点在第四限,
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△PBC=PM?OH+PM?HB=PM?(OH+HB)=PM?OB=PM,
∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,
∵PM=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,PMmax=,则S△PBC=×=,
此时P点坐标为(,﹣),S四边形ABPC=S△ABC+S△PBC=6+=,
即当P点坐标为(,﹣)时,四边形ABPC的面积最大,最大面积为;
(3)如图2,设直线m交y轴于点N,交直线l于点G,
则∠AGP=∠GNC+∠GCN,
当△AGB和△NGC相似时,必有∠AGB=∠CGB,
又∠AGB+∠CGB=180°,
∴∠AGB=∠CGB=90°,
∴∠ACO=∠OBN,
在Rt△AON和Rt△NOB中
∴Rt△AON≌Rt△NOB(ASA),
∴ON=OA=1,
∴N点坐标为(0,﹣1),
设直线m解析式为y=kx+d,把B、N两点坐标代入可得,解得,
∴直线m解析式为y=x﹣1,
即存在满足条件的直线m,其解析式为y=x﹣1.
【点评】本题为二次函数的综合应用,涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等.在(2)中确定出PM的值最时四边形ABPC的面积最大是解题的关键,在(3)中确定出满足条件的直线m的位置是解题的关键.本题考查知识点较多,综合性较强,特别是第(2)问和第(3)问难度较大.
同课章节目录
