2017年中考数学二轮专题复习讲义第15讲圆知识专题
文档属性
| 名称 | 2017年中考数学二轮专题复习讲义第15讲圆知识专题 |  | |
| 格式 | zip | ||
| 文件大小 | 244.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-02 09:39:14 | ||
图片预览




文档简介
2017年中考数学二轮专题复习讲义(15)关于圆的知识问题
【专题点拨】
圆是平面几何的重要图形,通常借助圆的对称性和旋转不变性,考查与圆有关的概念、性质、位置关系(尤其是切线的性质与判定),进行相关问题(正多边形、弧、扇形、圆锥等)的计算、作图、证明与探究.【解题策略】www.21-cn-jy.com
解决问题的关键是在具体情境中,综合运用所学知识(三角形、四边形、圆等),借助圆的性质、与圆有关的位置关系等,添加适当的辅助线构建相等的角、相等的边,或转化为直角三角形,或将立体图形(圆锥)转化为平面图形(扇形)进行分析与解决.
【典例解析】
类型一:圆的基本性质应用
例题1:(2016·四川泸州)如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG?BA=48,FG=,DF=2BF,求AH的值.
【解析】圆的综合题;三角形的外接圆与外心;切线的判定.(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得=求出BC,再由△BFC∽△BCD,得BC2=BF?BD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
【解答】(1)证明:连接CD,
∵BD是直径,
∴∠BCD=90°,即∠D+∠CBD=90°,
∵∠A=∠D,∠A=∠EBC,
∴∠CBD+∠EBC=90°,
∴BE⊥BD,
∴BE是⊙O切线.
(2)解:∵CG∥EB,
∴∠BCG=∠EBC,
∴∠A=∠BCG,
∵∠CBG=∠ABC
∴△ABC∽△CBG,
∴=,即BC2=BG?BA=48,
∴BC=4,
∵CG∥EB,
∴CF⊥BD,
∴△BFC∽△BCD,
∴BC2=BF?BD,
∵DF=2BF,
∴BF=4,
在RT△BCF中,CF==4,
∴CG=CF+FG=5,
在RT△BFG中,BG==3,
∵BG?BA=48,
∴即AG=5,
∴CG=AG,
∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,
∴∠CHF=∠CBF,
∴CH=CB=4,
∵△ABC∽△CBG,
∴=,
∴AC==,
∴AH=AC﹣CH=.
变式训练1:
(2016河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE= ;
②连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
类型二: 与圆相关的位置关系
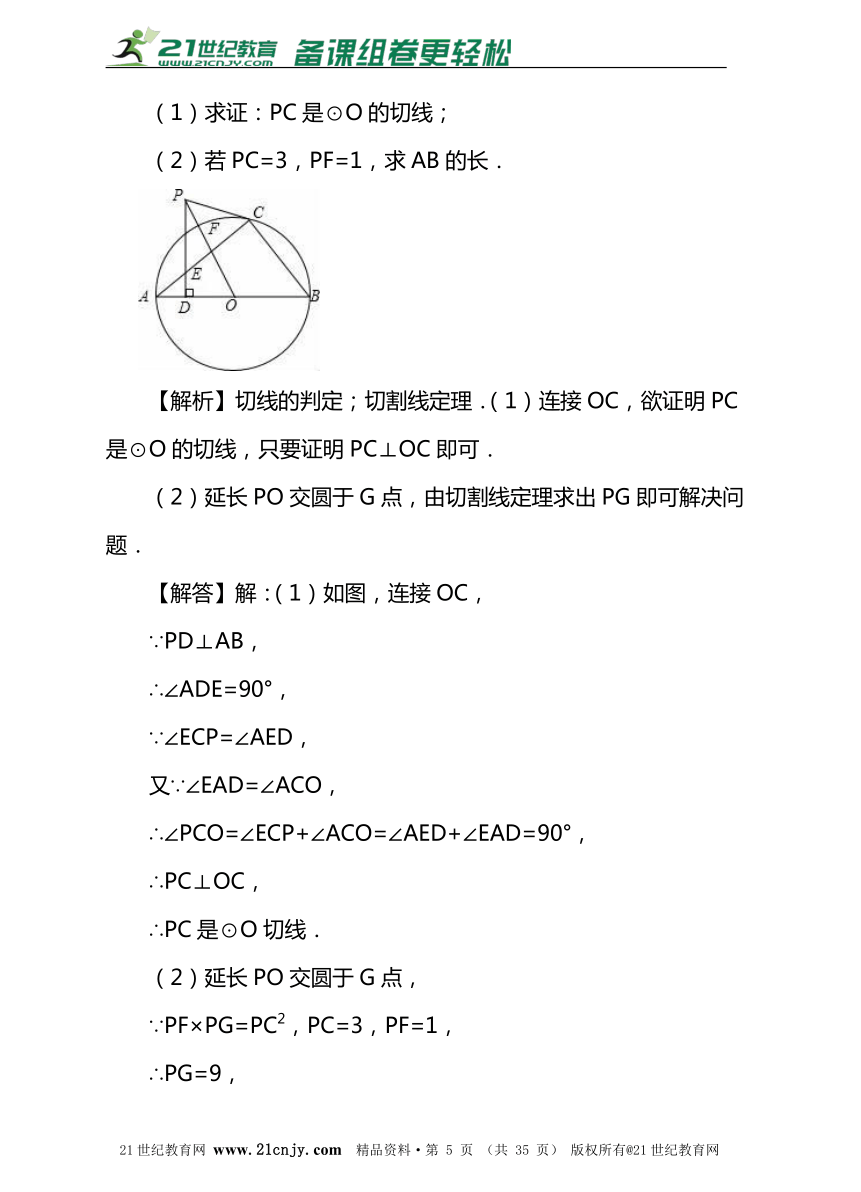
例题2:(2016·山东省菏泽市·3分)如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.21教育名师原创作品
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
【解析】切线的判定;切割线定理.(1)连接OC,欲证明PC是⊙O的切线,只要证明PC⊥OC即可.
(2)延长PO交圆于G点,由切割线定理求出PG即可解决问题.
【解答】解:(1)如图,连接OC,
∵PD⊥AB,
∴∠ADE=90°,
∵∠ECP=∠AED,
又∵∠EAD=∠ACO,
∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°,
∴PC⊥OC,
∴PC是⊙O切线.
(2)延长PO交圆于G点,
∵PF×PG=PC2,PC=3,PF=1,
∴PG=9,
∴FG=9﹣1=8,
∴AB=FG=8.
【点评】本题考查切线的判定、切割线定理、等角的余角相等等知识,解题的关键是熟练运用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.21·cn·jy·com
变式训练2:
(2016广西南宁)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(2016?南宁)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
类型三: 多边形与圆的问题
例题3:(2016·四川南充)如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 50 mm.
【解析】根据已知条件得到CM=30,AN=40,根据勾股定理列方程得到OM=40,由勾股定理得到结论.
【解答】解:如图,设圆心为O,
连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70﹣OM)2,
解得:OM=40,
∴OC==50,
∴能完全覆盖这个平面图形的圆面的最小半径是50mm.
故答案为:50.
【点评】本题考查的圆内接四边形,是垂径定理,根据题意画出图形,利用数形结合进行解答是解答此题的关键.
变式训练3:
(2015?辽宁抚顺)(第15题,3分)如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 .
类型四: 有圆有关的计算
例题4:(2016·云南省昆明市)如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
【解析】切线的判定;平行四边形的性质;扇形面积的计算.(1)欲证明CF是⊙O的切线,只要证明∠CDO=90°,只要证明△COD≌△COA即可.
(2)根据条件首先证明△OBD是等边三角形,∠FDB=∠EDC=∠ECD=30°,推出DE=EC=BO=BD=OA由此根据S阴=2?S△AOC﹣S扇形OAD即可解决问题.
【解答】(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,
∴OC∥BE,
∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DOC=∠AOC,
在△COD和△COA中,
,
∴△COD≌△COA,
∴∠CAO=∠CDO=90°,
∴CF⊥OD,
∴CF是⊙O的切线.
(2)解:∵∠F=30°,∠ODF=90°,
∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠DBO=60°,
∵∠DBO=∠F+∠FDB,
∴∠FDB=∠EDC=30°,
∵EC∥OB,
∴∠E=180°﹣∠OBD=120°,
∴∠ECD=180°﹣∠E﹣∠EDC=30°,
∴EC=ED=BO=DB,
∵EB=4,
∴OB=OD═OA=2,
在RT△AOC中,∵∠OAC=90°,OA=2,∠AOC=60°,
∴AC=OA?tan60°=2,
∴S阴=2?S△AOC﹣S扇形OAD=2××2×2﹣=2﹣.
变式训练4:
(2016·四川攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E21*cnjy*com
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
类型五: 圆的综合性问题
例题5:(2016·内蒙古包头)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
【解析】圆的综合题.(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;
(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;21教育网
(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
【解答】(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD=AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF==,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF=,
∵EF=,
∴DE=×=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴=,即GE?ED=AE?EB,
∴?GE=2,即GE=,
则GD=GE+ED=.
变式训练5:
(2016·辽宁丹东·10分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【能力检测】
1. (2016·山东省德州市·4分)正六边形的每个外角是 度.
2. (2016·广西百色·10分)如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
3. (2016·山东潍坊)正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:2-1-c-n-j-y
(1)四边形EBFD是矩形;
(2)DG=BE.
4. (2016·贵州安顺·12分)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=,BC=2,求⊙O的半径.
5. (2016·广西桂林·10分)如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【参考答案】
变式训练1:
(2016河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE= 2 ;
②连接OD,OE,当∠A的度数为 60° 时,四边形ODME是菱形.
【解析】菱形的判定.(1)先证明∠A=∠ABM,再证明∠MDE=∠MBA,∠MED=∠A即可解决问题.【来源:21·世纪·教育·网】
(2)①由DE∥AB,得=即可解决问题.
②当∠A=60°时,四边形ODME是菱形,只要证明△ODE,△DEM都是等边三角形即可.
【解答】(1)证明:∵∠ABC=90°,AM=MC,
∴BM=AM=MC,
∴∠A=∠ABM,
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
又∠ADE+∠MDE=180°,
∴∠MDE=∠MBA,
同理证明:∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME.
(2)①由(1)可知,∠A=∠MDE,
∴DE∥AB,
∴=,
∵AD=2DM,
∴DM:MA=1:3,
∴DE=AB=×6=2.
故答案为2.
②当∠A=60°时,四边形ODME是菱形.
理由:连接OD、OE,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE∥AB,
∴∠ODE=∠AOD=60°,∠MDE=∠MED=∠A=60°,
∴△ODE,△DEM都是等边三角形,
∴OD=OE=EM=DM,
∴四边形OEMD是菱形.
故答案为60°.
【点评】本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.2·1·c·n·j·y
变式训练2:
(2016广西南宁)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(2016?南宁)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
【解析】切线的判定.计算题;与圆有关的位置关系.(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直径,即可得证;
(2)由OD与BC平行得到三角形OAD与三角形BAC相似,由相似得比例求出OA的长,进而确定出AB的长,连接EF,过O作OG垂直于BC,利用勾股定理求出BG的长,由BG+GC求出BC的长,再由三角形BEF与三角形BAC相似,由相似得比例求出BE的长即可.
【解答】(1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线;
(2)解:过O作OG⊥BC,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∴BC=BG+GC=6+10=16,
∵OD∥BC,
∴△AOD∽△ABC,
∴=,即=,
解得:OA=,
∴AB=+10=,
连接EF,
∵BF为圆的直径,
∴∠BEF=90°,
∴∠BEF=∠C=90°,
∴EF∥AC,
∴=,即=,
解得:BE=12.
【点评】此题考查了切线的判定,相似三角形的判定与性质,平行线的判定与性质,以及等腰三角形的性质,熟练掌握切线的判定方法是解本题的关键.21世纪教育网版权所有
变式训练3:
(2015?辽宁抚顺)(第15题,3分)如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 2π﹣3 .21cnjy.com
解析: 此题是考查圆与正多边形结合的基本运算,空白正六边形为六个边长为2的正三角形,利用圆的面积公式和三角形的面积公式求得圆的面积和正六边形的面积,阴影面积=(圆的面积﹣正六边形的面积)×.www-2-1-cnjy-com
解:∵圆的半径为2,
∴面积为12π,
∵空白正六边形为六个边长为2的正三角形,
∴每个三角形面积为×2××sin60°=3,
∴正六边形面积为18,
∴阴影面积为(12π﹣18)×=2,
故答案为:2.
点评: 本题主要考查了正多边形和圆的面积公式,注意到阴影面积=(圆的面积﹣正六边形的面积)×是解答此题的关键.
变式训练4:
(2016·四川攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E【来源:21cnj*y.co*m】
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)【出处:21教育名师】
【解析】扇形面积的计算;全等三角形的判定与性质;矩形的性质.(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
在△ABF和△DEA中
,
∴△ABF≌△DEA(AAS),
∴DE=AB;
(2)解:∵BC=AD,AD=AF,
∴BC=AF,
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB==,
∴∠BAF=30°,
∵△ABF≌△DEA,
∴∠GDE=∠BAF=30°,DE=AB=DG=,
∴扇形ABG的面积==π.
【点评】本题考查了弧长公式,全等三角形的性质和判定,解直角三角形,勾股定理,矩形的性质的应用,能综合运用性质进行推理和计算是解此题的关键.
变式训练5:
(2016·辽宁丹东·10分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【解析】切线的性质;相似三角形的判定与性质.(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;
(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到,解方程即可得到结论.
【解答】(1)证明:连接OD,
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴,
∴EC2=DE?AE,
∴16=2(2+AD),
∴AD=6.
【能力检测】
1. (2016·山东省德州市·4分)正六边形的每个外角是 60 度.
【解析】多边形内角与外角.正多边形的外角和是360度,且每个外角都相等,据此即可求解.
【解答】解:正六边形的一个外角度数是:360÷6=60°.
故答案为:60.
【点评】本题考查了正多边形的外角的计算,理解外角和是360度,且每个外角都相等是关键.[
2. (2016·广西百色·10分)如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
【解析】切线的性质.(1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;
(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CA?CE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2+x)2,
解得:x=.
∴⊙O的半径为.
3. (2016·山东潍坊)正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:21·世纪*教育网
(1)四边形EBFD是矩形;
(2)DG=BE.
【考点】正方形的性质;矩形的判定;圆周角定理.
【分析】(1)直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,进而得出答案;21*cnjy*com
(2)直接利用正方形的性质的度数是90°,进而得出BE=DF,则BE=DG.
【解答】证明:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,
又∵DF∥BE,
∴∠EDF+∠BED=180°,
∴∠EDF=90°,
∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,
∴的度数是90°,
∴∠AFD=45°,
又∵∠GDF=90°,
∴∠DGF=∠DFC=45°,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
4. (2016·贵州安顺·12分)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.【版权所有:21教育】
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=,BC=2,求⊙O的半径.
【解析】(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=,然后根据勾股定理求得AC=,同理知DE=1;
方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即=r2+3,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
【解答】解:(1)直线CE与⊙O相切.…(1分)
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.…(5分)
(2)∵tan∠ACB==,BC=2,
∴AB=BC?tan∠ACB=,
∴AC=;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=,
∴DE=DC?tan∠DCE=1;
方法一:在Rt△CDE中,CE==,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即=r2+3
解得:r=
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM=AE=
在Rt△AMO中,OA==÷=…(9分)
【点评】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
5. (2016·广西桂林·10分)如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【解析】(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=AD=r,即点C在圆O上;
(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB==,则tan∠CDE=tan∠ACB=;
(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=,那么BF=BC+CF=.再证明四边形ABFE是矩形,得出AE=BF=,所以OG=AE=.
【解答】(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=AD=r,
∴点C在圆O上;
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB==,
∴tan∠CDE=tan∠ACB=;
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=AE.
易证△ABC∽△CFD,
∴=,即=,
∴CF=,
∴BF=BC+CF=8+=.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=,
∴OG=AE=,
即圆心O到弦ED的距离为.
【专题点拨】
圆是平面几何的重要图形,通常借助圆的对称性和旋转不变性,考查与圆有关的概念、性质、位置关系(尤其是切线的性质与判定),进行相关问题(正多边形、弧、扇形、圆锥等)的计算、作图、证明与探究.【解题策略】www.21-cn-jy.com
解决问题的关键是在具体情境中,综合运用所学知识(三角形、四边形、圆等),借助圆的性质、与圆有关的位置关系等,添加适当的辅助线构建相等的角、相等的边,或转化为直角三角形,或将立体图形(圆锥)转化为平面图形(扇形)进行分析与解决.
【典例解析】
类型一:圆的基本性质应用
例题1:(2016·四川泸州)如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG?BA=48,FG=,DF=2BF,求AH的值.
【解析】圆的综合题;三角形的外接圆与外心;切线的判定.(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得=求出BC,再由△BFC∽△BCD,得BC2=BF?BD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
【解答】(1)证明:连接CD,
∵BD是直径,
∴∠BCD=90°,即∠D+∠CBD=90°,
∵∠A=∠D,∠A=∠EBC,
∴∠CBD+∠EBC=90°,
∴BE⊥BD,
∴BE是⊙O切线.
(2)解:∵CG∥EB,
∴∠BCG=∠EBC,
∴∠A=∠BCG,
∵∠CBG=∠ABC
∴△ABC∽△CBG,
∴=,即BC2=BG?BA=48,
∴BC=4,
∵CG∥EB,
∴CF⊥BD,
∴△BFC∽△BCD,
∴BC2=BF?BD,
∵DF=2BF,
∴BF=4,
在RT△BCF中,CF==4,
∴CG=CF+FG=5,
在RT△BFG中,BG==3,
∵BG?BA=48,
∴即AG=5,
∴CG=AG,
∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,
∴∠CHF=∠CBF,
∴CH=CB=4,
∵△ABC∽△CBG,
∴=,
∴AC==,
∴AH=AC﹣CH=.
变式训练1:
(2016河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE= ;
②连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
类型二: 与圆相关的位置关系
例题2:(2016·山东省菏泽市·3分)如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.21教育名师原创作品
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
【解析】切线的判定;切割线定理.(1)连接OC,欲证明PC是⊙O的切线,只要证明PC⊥OC即可.
(2)延长PO交圆于G点,由切割线定理求出PG即可解决问题.
【解答】解:(1)如图,连接OC,
∵PD⊥AB,
∴∠ADE=90°,
∵∠ECP=∠AED,
又∵∠EAD=∠ACO,
∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°,
∴PC⊥OC,
∴PC是⊙O切线.
(2)延长PO交圆于G点,
∵PF×PG=PC2,PC=3,PF=1,
∴PG=9,
∴FG=9﹣1=8,
∴AB=FG=8.
【点评】本题考查切线的判定、切割线定理、等角的余角相等等知识,解题的关键是熟练运用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.21·cn·jy·com
变式训练2:
(2016广西南宁)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(2016?南宁)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
类型三: 多边形与圆的问题
例题3:(2016·四川南充)如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 50 mm.
【解析】根据已知条件得到CM=30,AN=40,根据勾股定理列方程得到OM=40,由勾股定理得到结论.
【解答】解:如图,设圆心为O,
连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70﹣OM)2,
解得:OM=40,
∴OC==50,
∴能完全覆盖这个平面图形的圆面的最小半径是50mm.
故答案为:50.
【点评】本题考查的圆内接四边形,是垂径定理,根据题意画出图形,利用数形结合进行解答是解答此题的关键.
变式训练3:
(2015?辽宁抚顺)(第15题,3分)如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 .
类型四: 有圆有关的计算
例题4:(2016·云南省昆明市)如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
【解析】切线的判定;平行四边形的性质;扇形面积的计算.(1)欲证明CF是⊙O的切线,只要证明∠CDO=90°,只要证明△COD≌△COA即可.
(2)根据条件首先证明△OBD是等边三角形,∠FDB=∠EDC=∠ECD=30°,推出DE=EC=BO=BD=OA由此根据S阴=2?S△AOC﹣S扇形OAD即可解决问题.
【解答】(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,
∴OC∥BE,
∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DOC=∠AOC,
在△COD和△COA中,
,
∴△COD≌△COA,
∴∠CAO=∠CDO=90°,
∴CF⊥OD,
∴CF是⊙O的切线.
(2)解:∵∠F=30°,∠ODF=90°,
∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠DBO=60°,
∵∠DBO=∠F+∠FDB,
∴∠FDB=∠EDC=30°,
∵EC∥OB,
∴∠E=180°﹣∠OBD=120°,
∴∠ECD=180°﹣∠E﹣∠EDC=30°,
∴EC=ED=BO=DB,
∵EB=4,
∴OB=OD═OA=2,
在RT△AOC中,∵∠OAC=90°,OA=2,∠AOC=60°,
∴AC=OA?tan60°=2,
∴S阴=2?S△AOC﹣S扇形OAD=2××2×2﹣=2﹣.
变式训练4:
(2016·四川攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E21*cnjy*com
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
类型五: 圆的综合性问题
例题5:(2016·内蒙古包头)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
【解析】圆的综合题.(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;
(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;21教育网
(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
【解答】(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD=AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF==,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF=,
∵EF=,
∴DE=×=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴=,即GE?ED=AE?EB,
∴?GE=2,即GE=,
则GD=GE+ED=.
变式训练5:
(2016·辽宁丹东·10分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【能力检测】
1. (2016·山东省德州市·4分)正六边形的每个外角是 度.
2. (2016·广西百色·10分)如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
3. (2016·山东潍坊)正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:2-1-c-n-j-y
(1)四边形EBFD是矩形;
(2)DG=BE.
4. (2016·贵州安顺·12分)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=,BC=2,求⊙O的半径.
5. (2016·广西桂林·10分)如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【参考答案】
变式训练1:
(2016河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE= 2 ;
②连接OD,OE,当∠A的度数为 60° 时,四边形ODME是菱形.
【解析】菱形的判定.(1)先证明∠A=∠ABM,再证明∠MDE=∠MBA,∠MED=∠A即可解决问题.【来源:21·世纪·教育·网】
(2)①由DE∥AB,得=即可解决问题.
②当∠A=60°时,四边形ODME是菱形,只要证明△ODE,△DEM都是等边三角形即可.
【解答】(1)证明:∵∠ABC=90°,AM=MC,
∴BM=AM=MC,
∴∠A=∠ABM,
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
又∠ADE+∠MDE=180°,
∴∠MDE=∠MBA,
同理证明:∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME.
(2)①由(1)可知,∠A=∠MDE,
∴DE∥AB,
∴=,
∵AD=2DM,
∴DM:MA=1:3,
∴DE=AB=×6=2.
故答案为2.
②当∠A=60°时,四边形ODME是菱形.
理由:连接OD、OE,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE∥AB,
∴∠ODE=∠AOD=60°,∠MDE=∠MED=∠A=60°,
∴△ODE,△DEM都是等边三角形,
∴OD=OE=EM=DM,
∴四边形OEMD是菱形.
故答案为60°.
【点评】本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.2·1·c·n·j·y
变式训练2:
(2016广西南宁)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(2016?南宁)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
【解析】切线的判定.计算题;与圆有关的位置关系.(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直径,即可得证;
(2)由OD与BC平行得到三角形OAD与三角形BAC相似,由相似得比例求出OA的长,进而确定出AB的长,连接EF,过O作OG垂直于BC,利用勾股定理求出BG的长,由BG+GC求出BC的长,再由三角形BEF与三角形BAC相似,由相似得比例求出BE的长即可.
【解答】(1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线;
(2)解:过O作OG⊥BC,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∴BC=BG+GC=6+10=16,
∵OD∥BC,
∴△AOD∽△ABC,
∴=,即=,
解得:OA=,
∴AB=+10=,
连接EF,
∵BF为圆的直径,
∴∠BEF=90°,
∴∠BEF=∠C=90°,
∴EF∥AC,
∴=,即=,
解得:BE=12.
【点评】此题考查了切线的判定,相似三角形的判定与性质,平行线的判定与性质,以及等腰三角形的性质,熟练掌握切线的判定方法是解本题的关键.21世纪教育网版权所有
变式训练3:
(2015?辽宁抚顺)(第15题,3分)如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 2π﹣3 .21cnjy.com
解析: 此题是考查圆与正多边形结合的基本运算,空白正六边形为六个边长为2的正三角形,利用圆的面积公式和三角形的面积公式求得圆的面积和正六边形的面积,阴影面积=(圆的面积﹣正六边形的面积)×.www-2-1-cnjy-com
解:∵圆的半径为2,
∴面积为12π,
∵空白正六边形为六个边长为2的正三角形,
∴每个三角形面积为×2××sin60°=3,
∴正六边形面积为18,
∴阴影面积为(12π﹣18)×=2,
故答案为:2.
点评: 本题主要考查了正多边形和圆的面积公式,注意到阴影面积=(圆的面积﹣正六边形的面积)×是解答此题的关键.
变式训练4:
(2016·四川攀枝花)如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E【来源:21cnj*y.co*m】
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)【出处:21教育名师】
【解析】扇形面积的计算;全等三角形的判定与性质;矩形的性质.(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
在△ABF和△DEA中
,
∴△ABF≌△DEA(AAS),
∴DE=AB;
(2)解:∵BC=AD,AD=AF,
∴BC=AF,
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB==,
∴∠BAF=30°,
∵△ABF≌△DEA,
∴∠GDE=∠BAF=30°,DE=AB=DG=,
∴扇形ABG的面积==π.
【点评】本题考查了弧长公式,全等三角形的性质和判定,解直角三角形,勾股定理,矩形的性质的应用,能综合运用性质进行推理和计算是解此题的关键.
变式训练5:
(2016·辽宁丹东·10分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【解析】切线的性质;相似三角形的判定与性质.(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;
(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到,解方程即可得到结论.
【解答】(1)证明:连接OD,
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴,
∴EC2=DE?AE,
∴16=2(2+AD),
∴AD=6.
【能力检测】
1. (2016·山东省德州市·4分)正六边形的每个外角是 60 度.
【解析】多边形内角与外角.正多边形的外角和是360度,且每个外角都相等,据此即可求解.
【解答】解:正六边形的一个外角度数是:360÷6=60°.
故答案为:60.
【点评】本题考查了正多边形的外角的计算,理解外角和是360度,且每个外角都相等是关键.[
2. (2016·广西百色·10分)如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
【解析】切线的性质.(1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;
(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CA?CE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2+x)2,
解得:x=.
∴⊙O的半径为.
3. (2016·山东潍坊)正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:21·世纪*教育网
(1)四边形EBFD是矩形;
(2)DG=BE.
【考点】正方形的性质;矩形的判定;圆周角定理.
【分析】(1)直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,进而得出答案;21*cnjy*com
(2)直接利用正方形的性质的度数是90°,进而得出BE=DF,则BE=DG.
【解答】证明:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,
又∵DF∥BE,
∴∠EDF+∠BED=180°,
∴∠EDF=90°,
∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,
∴的度数是90°,
∴∠AFD=45°,
又∵∠GDF=90°,
∴∠DGF=∠DFC=45°,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
4. (2016·贵州安顺·12分)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.【版权所有:21教育】
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=,BC=2,求⊙O的半径.
【解析】(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=,然后根据勾股定理求得AC=,同理知DE=1;
方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即=r2+3,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
【解答】解:(1)直线CE与⊙O相切.…(1分)
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.…(5分)
(2)∵tan∠ACB==,BC=2,
∴AB=BC?tan∠ACB=,
∴AC=;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=,
∴DE=DC?tan∠DCE=1;
方法一:在Rt△CDE中,CE==,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即=r2+3
解得:r=
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM=AE=
在Rt△AMO中,OA==÷=…(9分)
【点评】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
5. (2016·广西桂林·10分)如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【解析】(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=AD=r,即点C在圆O上;
(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB==,则tan∠CDE=tan∠ACB=;
(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=,那么BF=BC+CF=.再证明四边形ABFE是矩形,得出AE=BF=,所以OG=AE=.
【解答】(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=AD=r,
∴点C在圆O上;
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB==,
∴tan∠CDE=tan∠ACB=;
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=AE.
易证△ABC∽△CFD,
∴=,即=,
∴CF=,
∴BF=BC+CF=8+=.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=,
∴OG=AE=,
即圆心O到弦ED的距离为.
同课章节目录
