锐角三角函数 课件
图片预览





文档简介
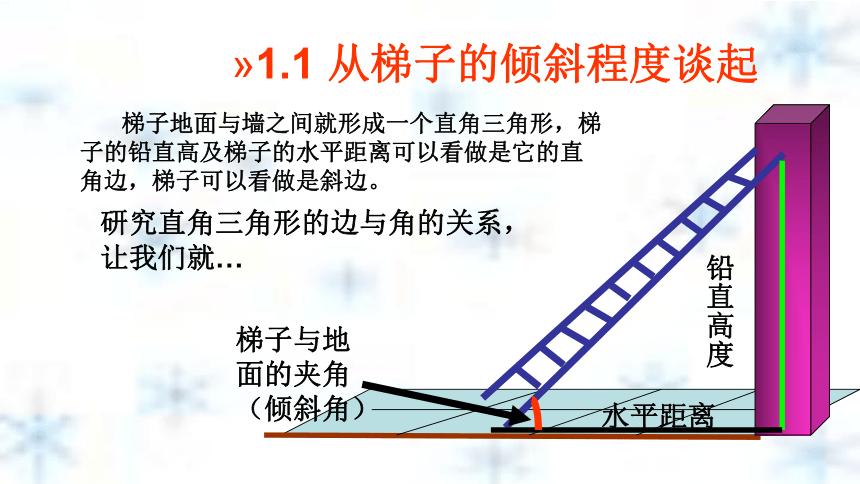
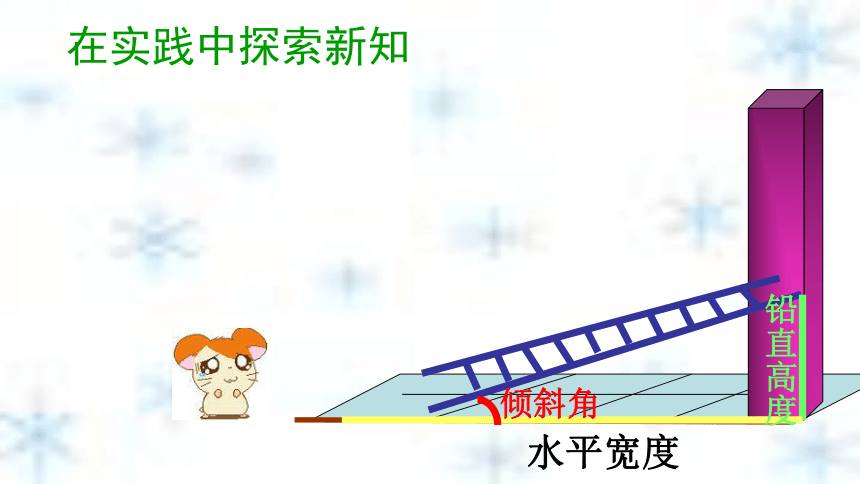
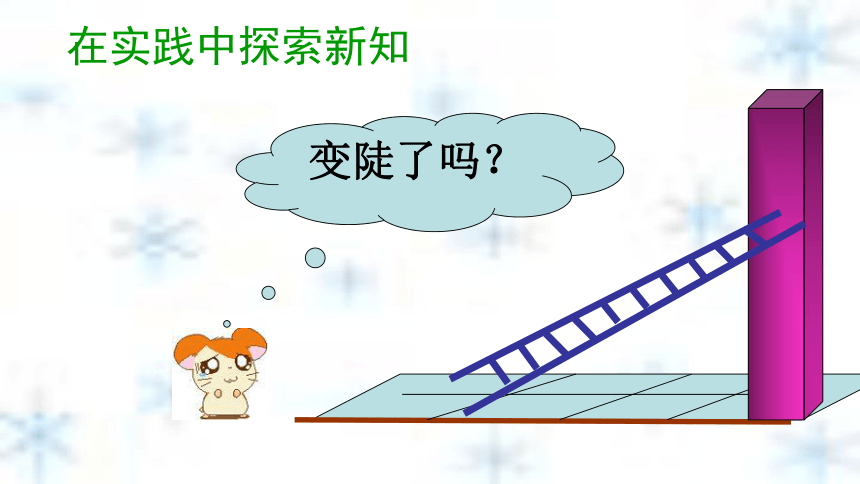
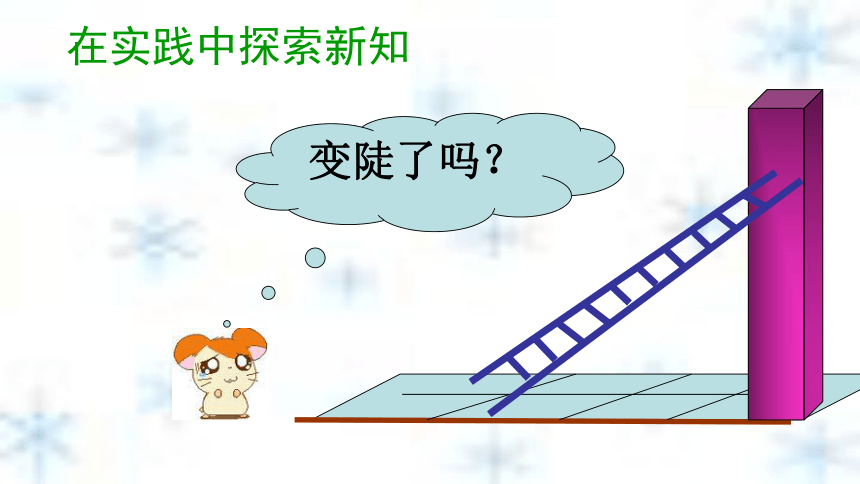
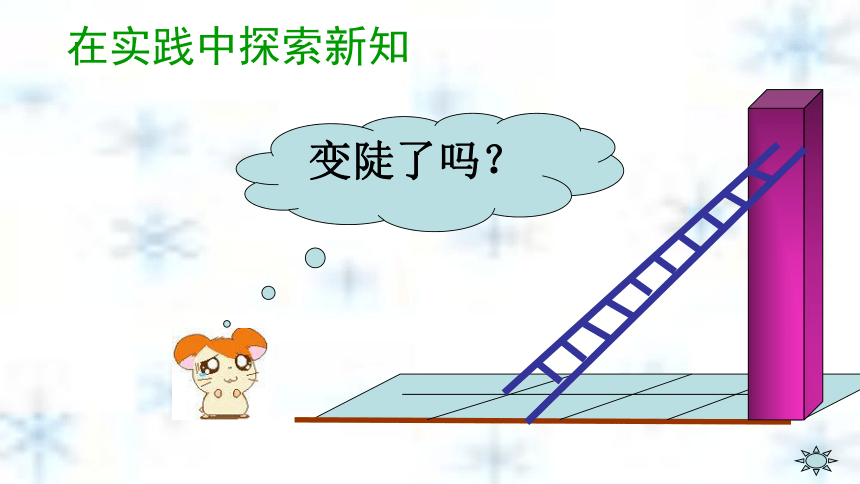
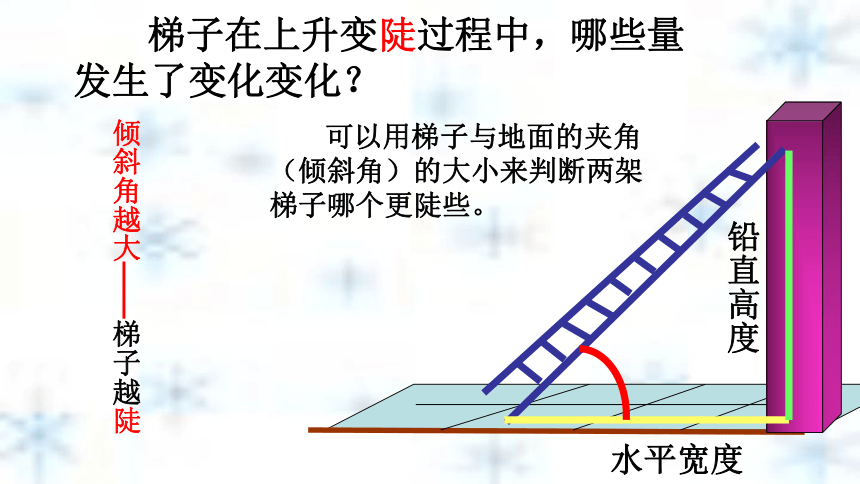
课件39张PPT。第一章 直角三角形的边角关系北师大版九年级下册第一章1.1锐角三角函数兴宁市大坪中学 练小盛1.1 从梯子的倾斜程度谈起 梯子地面与墙之间就形成一个直角三角形,梯子的铅直高及梯子的水平距离可以看做是它的直角边,梯子可以看做是斜边。铅直高度水平距离研究直角三角形的边与角的关系,让我们就…梯子与地面的夹角(倾斜角)水平宽度铅直高度倾斜角在实践中探索新知在实践中探索新知变陡了吗?在实践中探索新知变陡了吗?在实践中探索新知变陡了吗?在实践中探索新知变陡了吗? 梯子在上升变陡过程中,哪些量发生了变化变化? 铅直高度 水平宽度
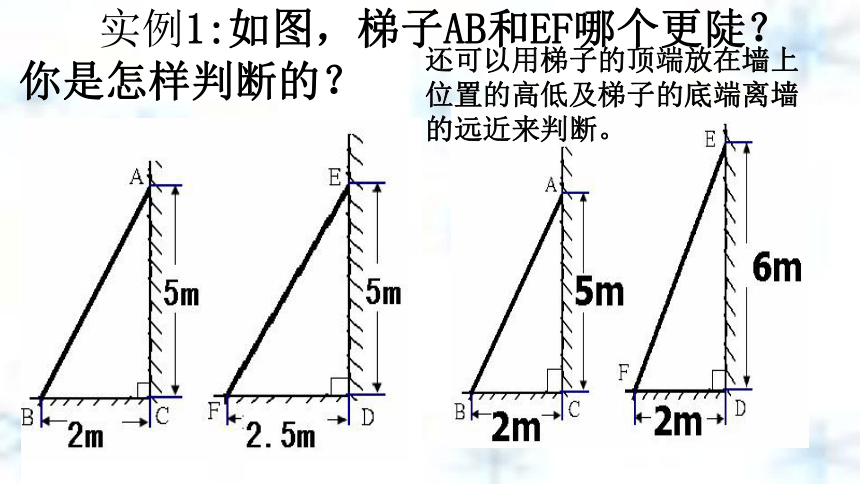
倾斜角越大——梯子越陡 可以用梯子与地面的夹角(倾斜角)的大小来判断两架梯子哪个更陡些。 实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?还可以用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断。 实例:如图,梯子AB和EF哪个更陡?你是怎样判断的?当铅直高度一样,水平宽度越小,梯子越陡当水平宽度一样,铅直高度越大,梯子越陡 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 水平宽度铅直高度倾斜角在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子的铅直高与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。小明和小亮这样想,如图:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.你同意小亮的看法吗?直角三角形的边与角的关系(1).Rt△AB1C1和Rt△AB2C2有什么关系? (3)如果改变B2在梯子上的位置(如B3C3 )呢?由此你得出什么结论?
相似相等? AB1 C1 C2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?任意改变B2在梯子上的位置,则:∠A的大小确定, ∠A的对边与邻边的比值不变。如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗? C2由此你得出什么结论?∠A的大小改变, ∠A的对边与邻边的比值随之改变。当直角三角形的锐角确定后,它的对边与邻边的比值也随之唯一确定;比值和三角形的大小无关,只和倾斜角的大小有关。B AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanA∠A的正切在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA读?tanA的值越大,梯子越陡.直角三角形中边与角的关系:锐角的三角函数--正切函数定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关如图,梯子AB1的倾斜程度与tanA有关吗?
与∠A有关吗?与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.例1 下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?解:甲梯中乙梯中∵ tanα> tanβ
∴甲梯更陡例2 如图,如图为拦水坝的横截面,拦水坝的坡度
i=1: ,若坝高 BC=20米,求坝面AB的长。
1.坡面与水平面的夹角(α)叫坡角
2.坡面的铅直高度与水平宽度的比称为坡度i
(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 4?2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).?回味无穷定义中应该注意的几个问题:1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.回味无穷回顾,反思,深化1.正切的定义:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即作业布置课本P4
习题1.1
1、2
倾斜角越大——梯子越陡 可以用梯子与地面的夹角(倾斜角)的大小来判断两架梯子哪个更陡些。 实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?还可以用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断。 实例:如图,梯子AB和EF哪个更陡?你是怎样判断的?当铅直高度一样,水平宽度越小,梯子越陡当水平宽度一样,铅直高度越大,梯子越陡 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 水平宽度铅直高度倾斜角在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子的铅直高与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。小明和小亮这样想,如图:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.你同意小亮的看法吗?直角三角形的边与角的关系(1).Rt△AB1C1和Rt△AB2C2有什么关系? (3)如果改变B2在梯子上的位置(如B3C3 )呢?由此你得出什么结论?
相似相等? AB1 C1 C2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?任意改变B2在梯子上的位置,则:∠A的大小确定, ∠A的对边与邻边的比值不变。如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗? C2由此你得出什么结论?∠A的大小改变, ∠A的对边与邻边的比值随之改变。当直角三角形的锐角确定后,它的对边与邻边的比值也随之唯一确定;比值和三角形的大小无关,只和倾斜角的大小有关。B AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanA∠A的正切在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA读?tanA的值越大,梯子越陡.直角三角形中边与角的关系:锐角的三角函数--正切函数定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关如图,梯子AB1的倾斜程度与tanA有关吗?
与∠A有关吗?与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.例1 下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?解:甲梯中乙梯中∵ tanα> tanβ
∴甲梯更陡例2 如图,如图为拦水坝的横截面,拦水坝的坡度
i=1: ,若坝高 BC=20米,求坝面AB的长。
1.坡面与水平面的夹角(α)叫坡角
2.坡面的铅直高度与水平宽度的比称为坡度i
(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 4?2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).?回味无穷定义中应该注意的几个问题:1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.回味无穷回顾,反思,深化1.正切的定义:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即作业布置课本P4
习题1.1
1、2
