第六章 特殊平行四边形 单元测试卷
图片预览
文档简介
第六章 特殊平行四边形 单元测试卷
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
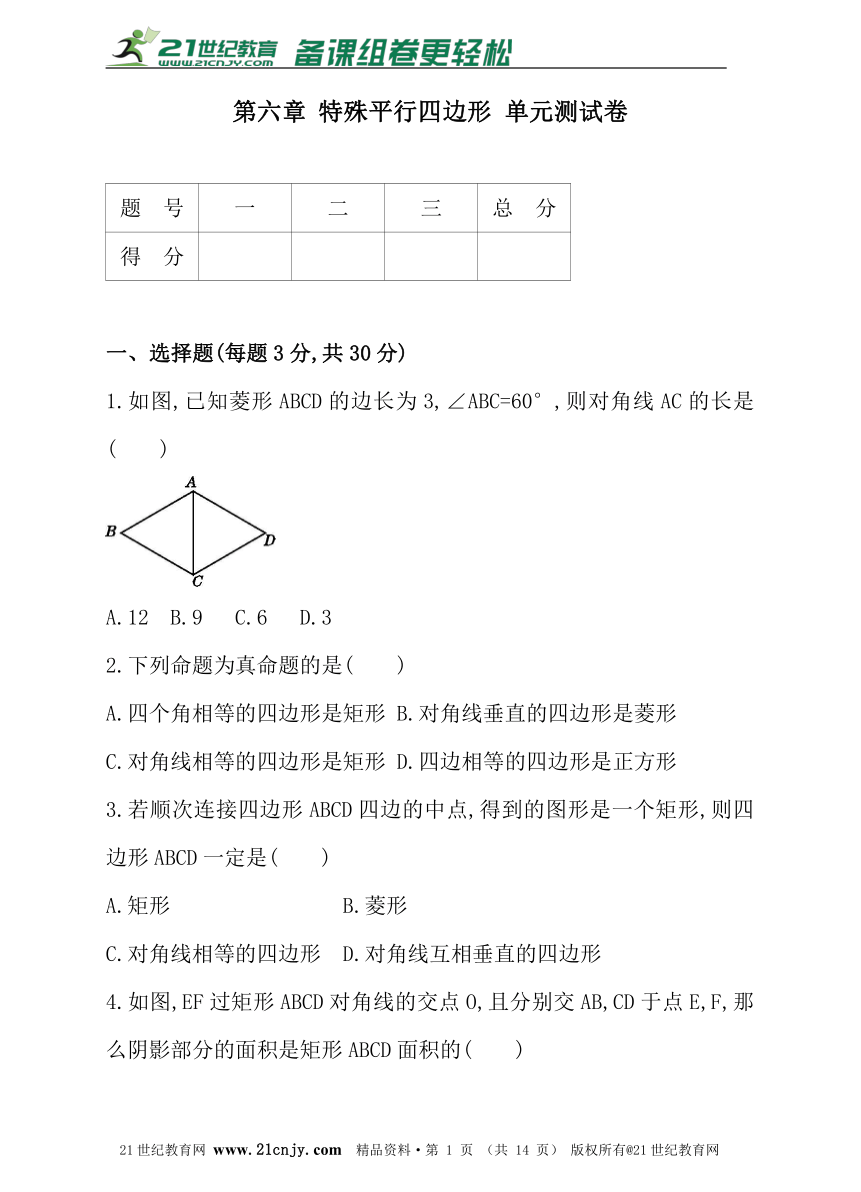
1.如图,已知菱形ABCD的边长为3,∠ABC=60°,则对角线AC的长是( )
A.12 B.9 C.6 D.3
2.下列命题为真命题的是( )
A.四个角相等的四边形是矩形 B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.四边相等的四边形是正方形
3.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线相等的四边形 D.对角线互相垂直的四边形
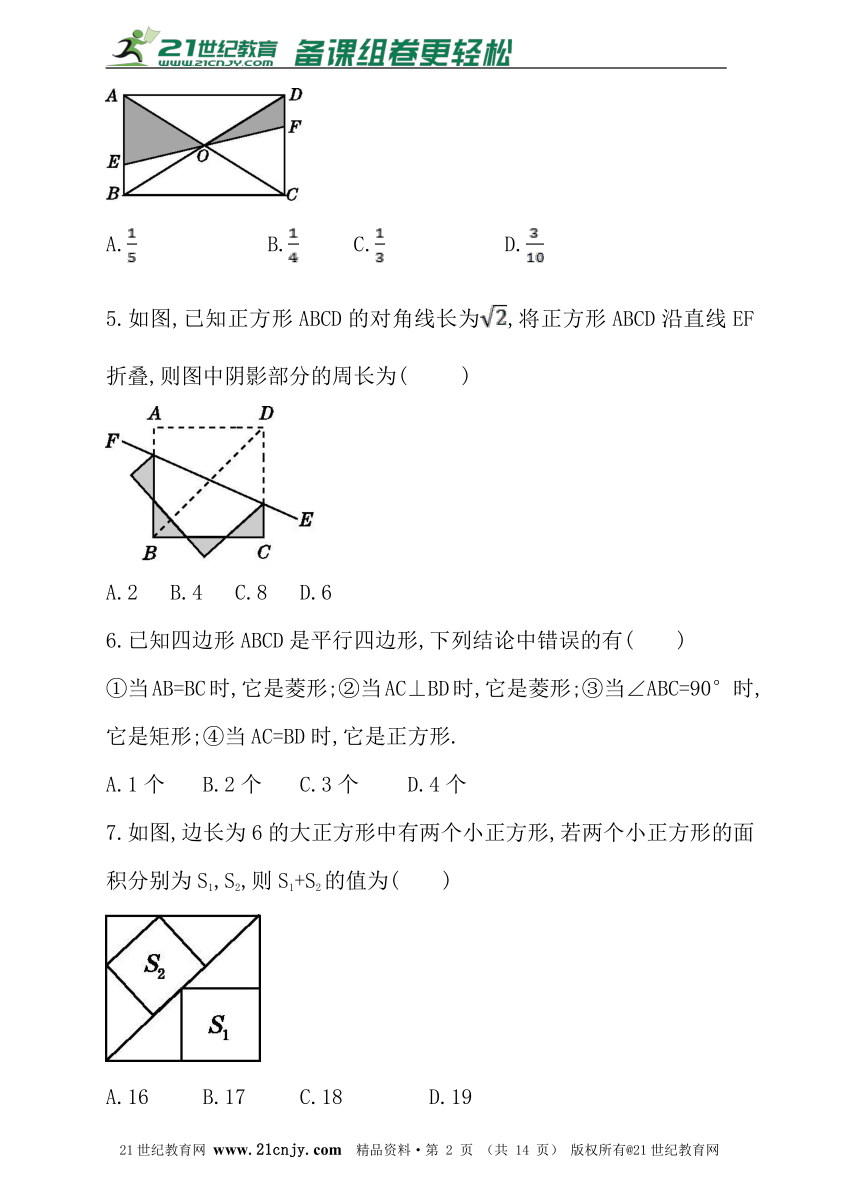
4.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( )2·1·c·n·j·y
A. B. C. D.
5.如图,已知正方形ABCD的对角线长为,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为( )2-1-c-n-j-y
A.2 B.4 C.8 D.6
6.已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.21*cnjy*com
A.1个 B.2个 C.3个 D.4个
7.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )【来源:21cnj*y.co*m】
A.16 B.17 C.18 D.19
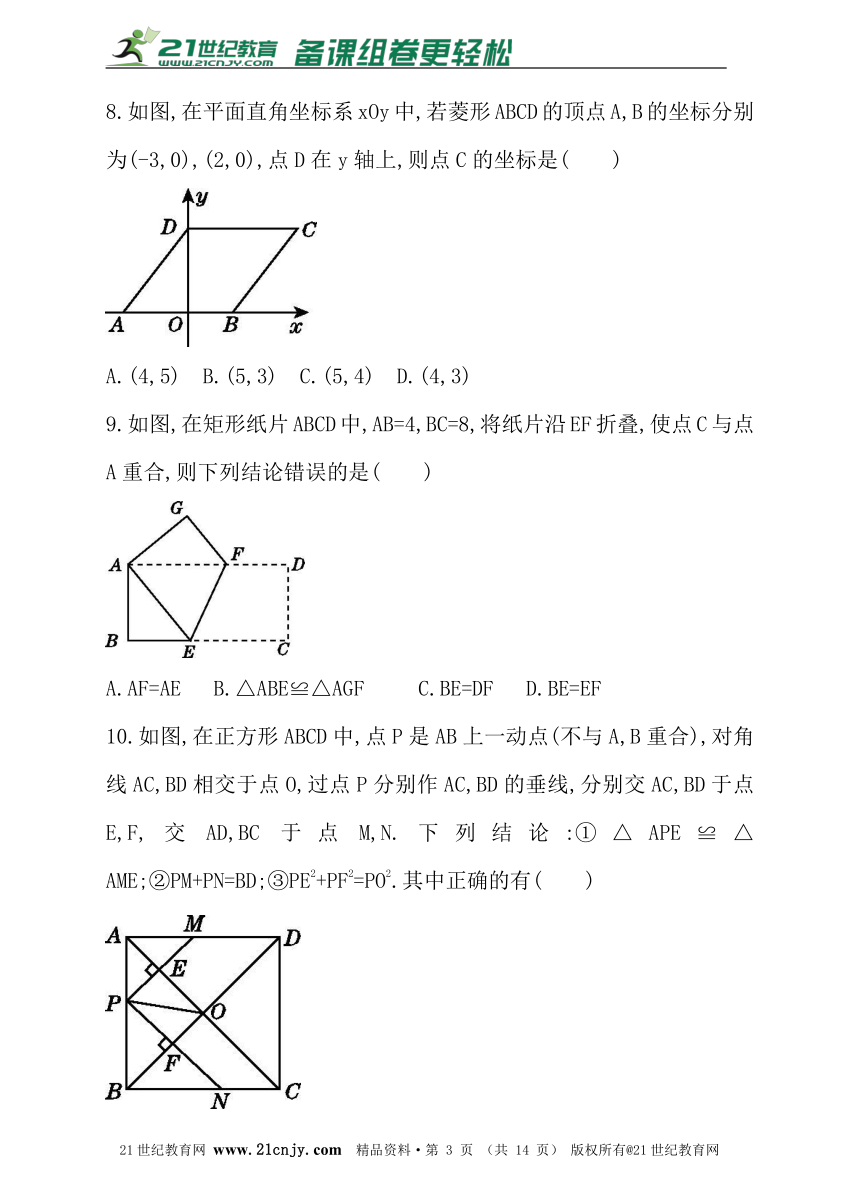
8.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是( )
A.(4,5) B.(5,3) C.(5,4) D.(4,3)
9.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )【出处:21教育名师】
A.AF=AE B.△ABE≌△AGF C.BE=DF D.BE=EF
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题3分,共24分)
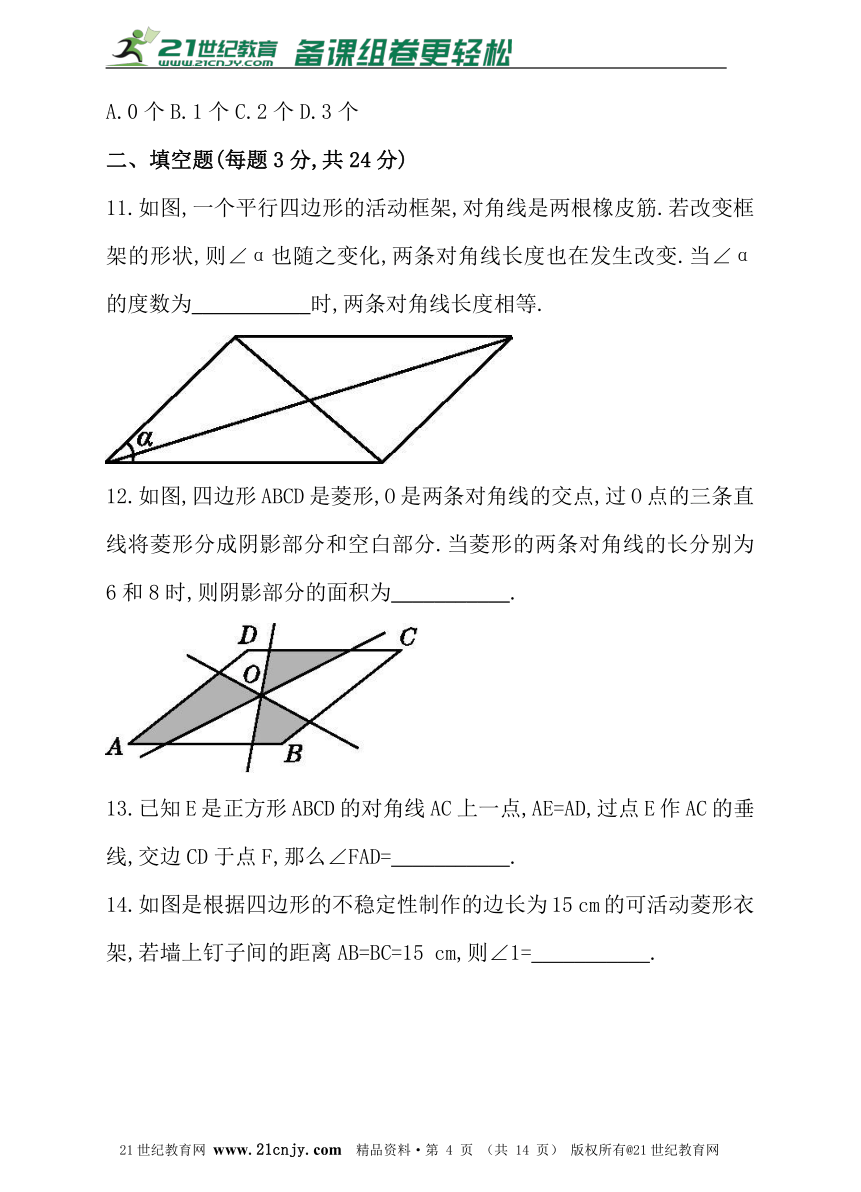
11.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α的度数为___________时,两条对角线长度相等.【版权所有:21教育】
12.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为___________.21教育网
13.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD=___________.?21*cnjy*com
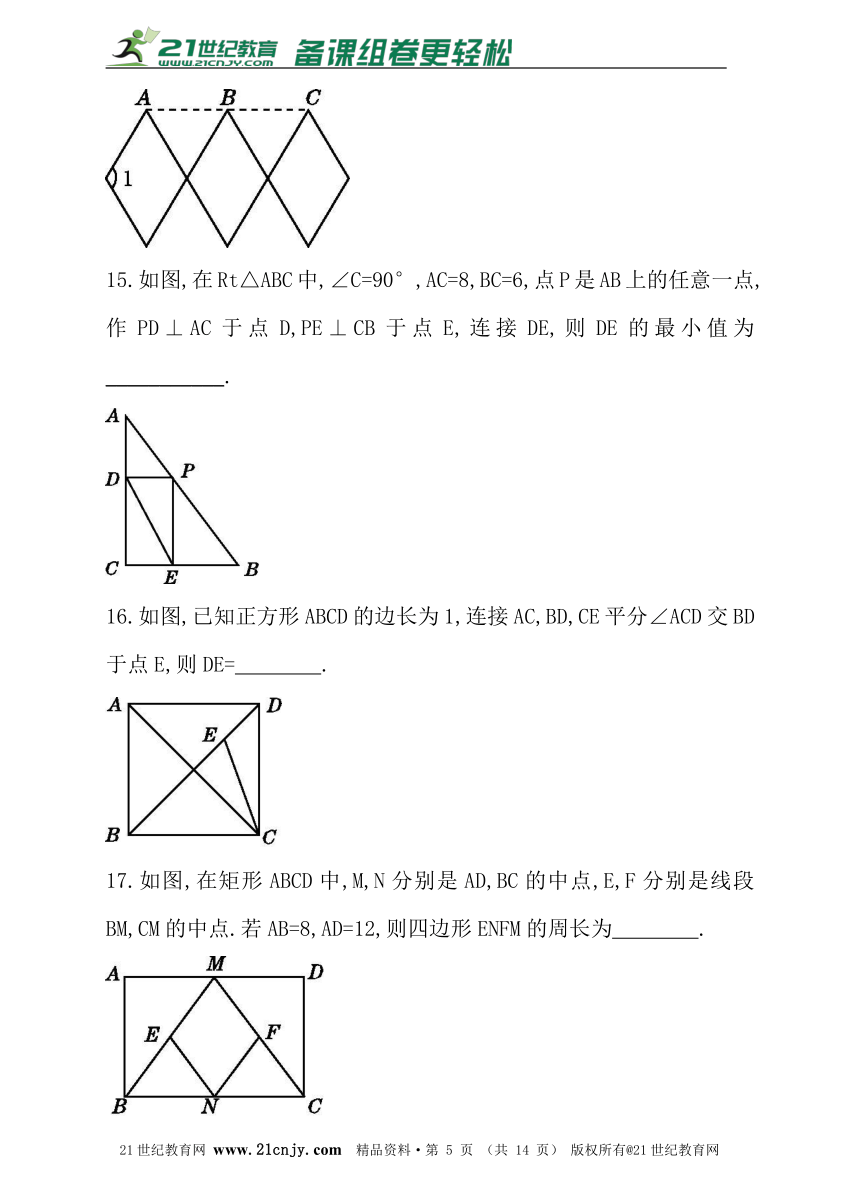
14.如图是根据四边形的不稳定性制作的边长为15 cm的可活动菱形衣架,若墙上钉子间的距离AB=BC=15 cm,则∠1=___________.
?
15.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为___________.?
16.如图,已知正方形ABCD的边长为1,连接AC,BD,CE平分∠ACD交BD于点E,则DE= .
17.如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点.若AB=8,AD=12,则四边形ENFM的周长为 .
18.如图,在边长为2的菱形 ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,……,按此规律所作的第n个菱形的边长是 .
三、解答题(19,20题每题9分,21题 10分,22,23题每题12分,24题14分,共66分)
19.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.求证:BD=CE.21教育名师原创作品
20.如图所示,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH.求证:∠DHO=∠DCO.
21.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.
22.如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.
23.如图所示,把一张矩形纸片ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)线段BF与DF相等吗?请说明理由.
(2)若将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,试判断四边形BGDF的形状,并说明理由.21·世纪*教育网
(3)若AB=4,AD=8,在(2)的条件下,求线段DG的长.
24.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE__________是菱形(填“可能”或“不可能”).请说明理由.?
参考答案
一、1.【答案】D 2.【答案】A
3.【答案】D
解:首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
4.【答案】B 5.【答案】B
6.【答案】A
解:①当AB=BC时,它是菱形,正确;②当AC⊥BD时,它是菱形,正确;③当∠ABC=90°时,它是矩形,正确;④当AC=BD时,它是矩形,因此④是错误的.
7.【答案】B 8.【答案】C 9.【答案】D
10.【答案】D
解:∵四边形ABCD是正方形,∴∠PAE=∠MAE=45°.
∵PM⊥AC,∴∠PEA=∠MEA.
又∵AE=AE,∴根据“ASA”可得△APE≌△AME.故①正确;由①得PE=ME,∴PM=2PE.同理PN=2PF,又易知PF=BF,四边形PEOF是矩形,∴PN=2BF,PM=2FO.∴PM+PN=2FO+2BF=2BO=BD.故②正确;在Rt△PFO中,∵FO2+PF2=PO2,而PE=FO,∴PE2+PF2=PO2.故③正确.
二、11.【答案】90°
解:对角线相等的平行四边形是矩形.
12.【答案】12
解:∵菱形的两条对角线的长分别为6和8,∴菱形的面积=×6×8=24.∵O是菱形两条对角线的交点,∴阴影部分的面积=×24=12.
13.【答案】22.5°
解:如图,由四边形ABCD是正方形,可知∠BAD=∠D=90°,∠CAD=∠BAD=45°.
由FE⊥AC,可知∠AEF=90°.
在Rt△AEF与Rt△ADF中, AE=AD,AF=AF,∴Rt△AEF≌Rt△ADF(HL).
∴∠FAD=∠FAE=∠CAD=×45°=22.5°.
14.【答案】120° 15.【答案】4.8 16.【答案】-1
17.【答案】20
解:点N是BC的中点,点E,F分别是BM,CM的中点,由三角形的中位线定理可证EN∥MC,NF∥ME,EN=MC,FN=MB.又易知MB=MC,所以四边形ENFM是菱形.由点M是AD的中点,AD=12得AM=6.在Rt△ABM中,由勾股定理得BM=10.因为点E是BM的中点,所以EM=5,所以四边形ENFM的周长为20.21cnjy.com
18.【答案】(2)n-1
三、19.证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
又∵BE=AB,∴BE=CD.
∴四边形BECD是平行四边形.
∴BD=CE.
20.证明:∵四边形ABCD是菱形,
∴AB∥CD,OD=OB,AC⊥BD.
∵DH⊥AB,
∴∠AHD=∠BHD=90°.
∴∠BDH+∠ODC=90°.
∵∠DCO+∠ODC=90°,
∴∠BDH=∠DCO.
在Rt△BHD中,OB=OD,
∴OH=OD.∴∠DHO=∠BDH.
∴∠DHO=∠DCO.
21.(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形.
∵四边形ABCD为矩形,∴OD=OC.
∴四边形OCED为菱形.
(2)解:∵四边形ABCD为矩形,
∴BO=DO=BD.
∴S△OCD=S△OCB=S△ABC=××3×4=3.
∴S菱形OCED=2S△OCD=6.
22.(1)证明:在△BCE与△DCF中,
∴△BCE≌△DCF.
(2)解:∵△BCE≌△DCF,
∴∠EBC=∠FDC=30°.
∵∠BCD=90°,∴∠BEC=60°.
∵EC=FC,
∴∠CEF=45°.∴∠BEF=105°.
23.解:(1)相等.
理由:∵在△ABF和△EDF中,∠A=∠E=∠C=90°,∠AFB=∠EFD,
AB=ED=CD,
∴△ABF≌△EDF.∴BF=DF.
(2)四边形BGDF是菱形.
理由:由四边形ABCD是矩形,易得AD∥BC,则BG∥DF.
∵△BCD沿BD折叠之后得到△BED,∴BC=BE.而恢复原状后,点F与点G重合,则BG=BF,而由(1)得BF=DF,∴BG=DF.21·cn·jy·com
∴四边形BGDF为平行四边形.
又∵BF=DF,
∴四边形BGDF为菱形.
(3)由(2)知DG=BG,
∴CG=8-DG.
又∵CD2+GC2=DG2,即42+(8-DG)2=DG2,解得DG=5.
24.解:(1)OE=OF.证明如下:∵CE是∠ACB的平分线,∴∠ACE=∠BCE.又∵MN∥BC,∴∠NEC=∠ECB.21世纪教育网版权所有
∴∠NEC=∠ACE.∴OE=OC.
∵CF是∠ACD的平分线,
∴∠OCF=∠FCD.又∵MN∥BC,∴∠OFC=∠FCD.∴∠OFC=∠OCF.∴OF=OC.∴OE=OF.www.21-cn-jy.com
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO.
∴AO+CO=EO+FO,即AC=EF.
∴四边形AECF是矩形.已知MN∥BC,当∠ACB=90°时,∠AOE=90°,∴AC⊥EF.∴四边形AECF是正方形.【来源:21·世纪·教育·网】
(3)不可能.理由如下:
连接BF,∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°.若四边形BCFE是菱形,则BF⊥EC.但在一个三角形中,不可能存在两个角为90°,故四边形BCFE不可能为菱形.www-2-1-cnjy-com
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.如图,已知菱形ABCD的边长为3,∠ABC=60°,则对角线AC的长是( )
A.12 B.9 C.6 D.3
2.下列命题为真命题的是( )
A.四个角相等的四边形是矩形 B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.四边相等的四边形是正方形
3.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线相等的四边形 D.对角线互相垂直的四边形
4.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( )2·1·c·n·j·y
A. B. C. D.
5.如图,已知正方形ABCD的对角线长为,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为( )2-1-c-n-j-y
A.2 B.4 C.8 D.6
6.已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.21*cnjy*com
A.1个 B.2个 C.3个 D.4个
7.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )【来源:21cnj*y.co*m】
A.16 B.17 C.18 D.19
8.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是( )
A.(4,5) B.(5,3) C.(5,4) D.(4,3)
9.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )【出处:21教育名师】
A.AF=AE B.△ABE≌△AGF C.BE=DF D.BE=EF
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题3分,共24分)
11.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α的度数为___________时,两条对角线长度相等.【版权所有:21教育】
12.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为___________.21教育网
13.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD=___________.?21*cnjy*com
14.如图是根据四边形的不稳定性制作的边长为15 cm的可活动菱形衣架,若墙上钉子间的距离AB=BC=15 cm,则∠1=___________.
?
15.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为___________.?
16.如图,已知正方形ABCD的边长为1,连接AC,BD,CE平分∠ACD交BD于点E,则DE= .
17.如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点.若AB=8,AD=12,则四边形ENFM的周长为 .
18.如图,在边长为2的菱形 ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,……,按此规律所作的第n个菱形的边长是 .
三、解答题(19,20题每题9分,21题 10分,22,23题每题12分,24题14分,共66分)
19.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.求证:BD=CE.21教育名师原创作品
20.如图所示,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH.求证:∠DHO=∠DCO.
21.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.
22.如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.
23.如图所示,把一张矩形纸片ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)线段BF与DF相等吗?请说明理由.
(2)若将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,试判断四边形BGDF的形状,并说明理由.21·世纪*教育网
(3)若AB=4,AD=8,在(2)的条件下,求线段DG的长.
24.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE__________是菱形(填“可能”或“不可能”).请说明理由.?
参考答案
一、1.【答案】D 2.【答案】A
3.【答案】D
解:首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
4.【答案】B 5.【答案】B
6.【答案】A
解:①当AB=BC时,它是菱形,正确;②当AC⊥BD时,它是菱形,正确;③当∠ABC=90°时,它是矩形,正确;④当AC=BD时,它是矩形,因此④是错误的.
7.【答案】B 8.【答案】C 9.【答案】D
10.【答案】D
解:∵四边形ABCD是正方形,∴∠PAE=∠MAE=45°.
∵PM⊥AC,∴∠PEA=∠MEA.
又∵AE=AE,∴根据“ASA”可得△APE≌△AME.故①正确;由①得PE=ME,∴PM=2PE.同理PN=2PF,又易知PF=BF,四边形PEOF是矩形,∴PN=2BF,PM=2FO.∴PM+PN=2FO+2BF=2BO=BD.故②正确;在Rt△PFO中,∵FO2+PF2=PO2,而PE=FO,∴PE2+PF2=PO2.故③正确.
二、11.【答案】90°
解:对角线相等的平行四边形是矩形.
12.【答案】12
解:∵菱形的两条对角线的长分别为6和8,∴菱形的面积=×6×8=24.∵O是菱形两条对角线的交点,∴阴影部分的面积=×24=12.
13.【答案】22.5°
解:如图,由四边形ABCD是正方形,可知∠BAD=∠D=90°,∠CAD=∠BAD=45°.
由FE⊥AC,可知∠AEF=90°.
在Rt△AEF与Rt△ADF中, AE=AD,AF=AF,∴Rt△AEF≌Rt△ADF(HL).
∴∠FAD=∠FAE=∠CAD=×45°=22.5°.
14.【答案】120° 15.【答案】4.8 16.【答案】-1
17.【答案】20
解:点N是BC的中点,点E,F分别是BM,CM的中点,由三角形的中位线定理可证EN∥MC,NF∥ME,EN=MC,FN=MB.又易知MB=MC,所以四边形ENFM是菱形.由点M是AD的中点,AD=12得AM=6.在Rt△ABM中,由勾股定理得BM=10.因为点E是BM的中点,所以EM=5,所以四边形ENFM的周长为20.21cnjy.com
18.【答案】(2)n-1
三、19.证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
又∵BE=AB,∴BE=CD.
∴四边形BECD是平行四边形.
∴BD=CE.
20.证明:∵四边形ABCD是菱形,
∴AB∥CD,OD=OB,AC⊥BD.
∵DH⊥AB,
∴∠AHD=∠BHD=90°.
∴∠BDH+∠ODC=90°.
∵∠DCO+∠ODC=90°,
∴∠BDH=∠DCO.
在Rt△BHD中,OB=OD,
∴OH=OD.∴∠DHO=∠BDH.
∴∠DHO=∠DCO.
21.(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形.
∵四边形ABCD为矩形,∴OD=OC.
∴四边形OCED为菱形.
(2)解:∵四边形ABCD为矩形,
∴BO=DO=BD.
∴S△OCD=S△OCB=S△ABC=××3×4=3.
∴S菱形OCED=2S△OCD=6.
22.(1)证明:在△BCE与△DCF中,
∴△BCE≌△DCF.
(2)解:∵△BCE≌△DCF,
∴∠EBC=∠FDC=30°.
∵∠BCD=90°,∴∠BEC=60°.
∵EC=FC,
∴∠CEF=45°.∴∠BEF=105°.
23.解:(1)相等.
理由:∵在△ABF和△EDF中,∠A=∠E=∠C=90°,∠AFB=∠EFD,
AB=ED=CD,
∴△ABF≌△EDF.∴BF=DF.
(2)四边形BGDF是菱形.
理由:由四边形ABCD是矩形,易得AD∥BC,则BG∥DF.
∵△BCD沿BD折叠之后得到△BED,∴BC=BE.而恢复原状后,点F与点G重合,则BG=BF,而由(1)得BF=DF,∴BG=DF.21·cn·jy·com
∴四边形BGDF为平行四边形.
又∵BF=DF,
∴四边形BGDF为菱形.
(3)由(2)知DG=BG,
∴CG=8-DG.
又∵CD2+GC2=DG2,即42+(8-DG)2=DG2,解得DG=5.
24.解:(1)OE=OF.证明如下:∵CE是∠ACB的平分线,∴∠ACE=∠BCE.又∵MN∥BC,∴∠NEC=∠ECB.21世纪教育网版权所有
∴∠NEC=∠ACE.∴OE=OC.
∵CF是∠ACD的平分线,
∴∠OCF=∠FCD.又∵MN∥BC,∴∠OFC=∠FCD.∴∠OFC=∠OCF.∴OF=OC.∴OE=OF.www.21-cn-jy.com
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO.
∴AO+CO=EO+FO,即AC=EF.
∴四边形AECF是矩形.已知MN∥BC,当∠ACB=90°时,∠AOE=90°,∴AC⊥EF.∴四边形AECF是正方形.【来源:21·世纪·教育·网】
(3)不可能.理由如下:
连接BF,∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°.若四边形BCFE是菱形,则BF⊥EC.但在一个三角形中,不可能存在两个角为90°,故四边形BCFE不可能为菱形.www-2-1-cnjy-com
