6.2.1 频率的稳定性 同步练习

6.2.1 频率的稳定性
基础训练
1.小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A表示正面朝上这一事件,则事件A发生的(　　)
A.频率是0.4 B.频率是0.6
C.频率是6 D.频率接近0.6
2.小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间
x/min
051015频数
(通话次数)
20
16
9
5
则通话时间不超过15 min的频率为(　　)
A.0.1 B.0.4 C.0.5 D.0.9
3.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12,10,6,8,则第5组的频率是(　　)21世纪教育网版权所有
A.0.1 B.0.2 C.0.3 D.0.4
4.现有50张大小、质地及背面图案均相同的《西游记》人物卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为　　　　.?21·cn·jy·com
5.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表.www.21-cn-jy.com
摸球
总次数
10
20
30
60
90
120
180
240
330
450
“和为8”出
现的次数
2
10
13
24
30
37
58
82
110
150
“和为8”出
现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33
(1)10次试验“和为8”出现的频率是_____________,20次试验“和为
8”出现的频率是_____________,450次试验“和为8”出现的频率是
_____________;?
(2)如果试验继续进行下去,根据上表数据,估计出现“和为8”的频率
是_____________.?
6.某人在做掷硬币试验时,投掷m次,正面朝上有n次
,则下列说法中正确的是(　　)
A.P一定等于
B.P一定不等于
C.多投一次,P更接近
D.随投掷次数逐渐增加,P在附近摆动
7.在一个不透明的盒子里装着若干个白球,小明想估计其中的白球数,于是他放入10个黑球,搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,得到如下数据:21教育网
摸球的
次数n
20
40
60
80
120
160
200
摸到白球
的次数m
15
33
49
63
97
128
158
摸到白球
的频率
0.75
0.83
0.82
0.79
0.81
0.80
0.79
估计盒子里白球的个数为(　　)
A.8　　B.40　　C.80　　D.无法估计
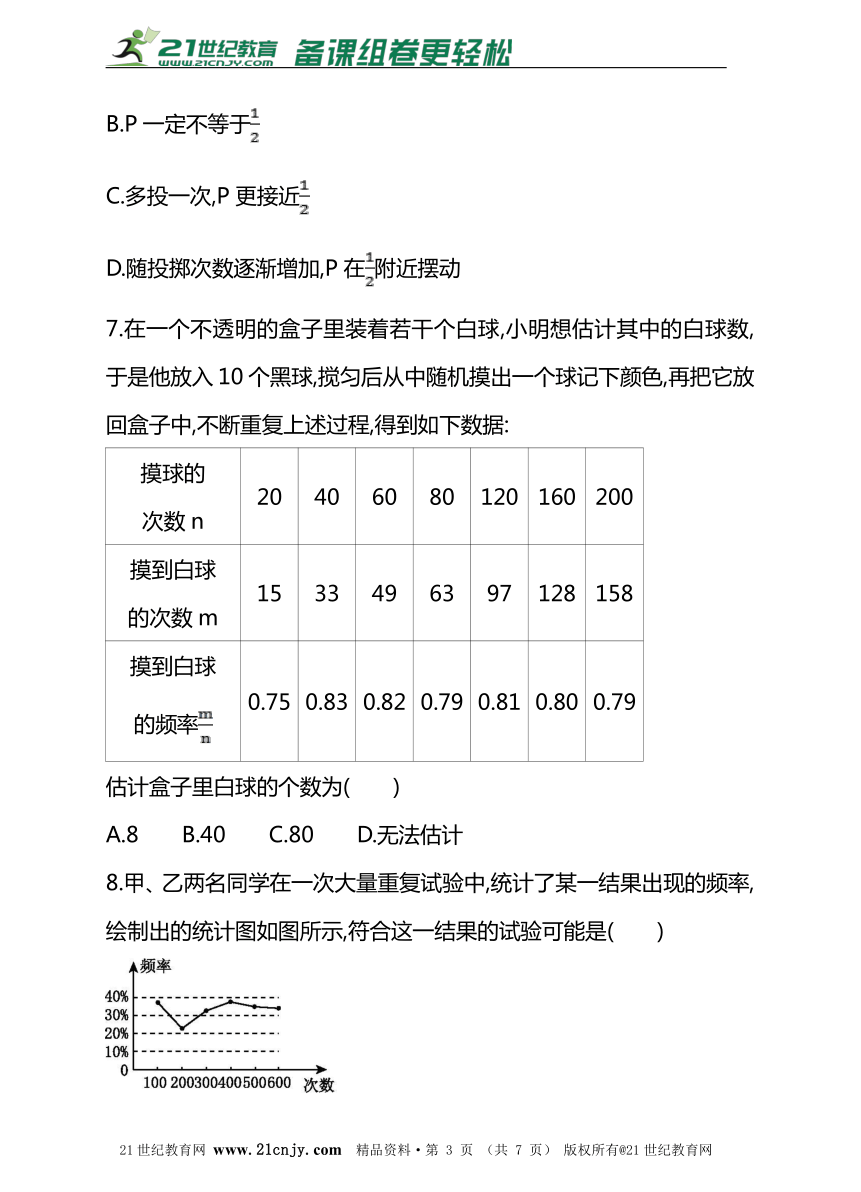
8.甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一结果的试验可能是(　　)
A.掷一枚质地均匀的骰子,出现1点朝上的频率
B.任意写一个正整数,它能被3整除的频率
C.抛一枚硬币,出现正面朝上的频率
D.从一个装有2个白球和1个红球的袋子中任取一球,取到白球的频率
提升训练
9.一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n的值.21cnjy.com
10.研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
11.某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
转动转盘
的次数n
100
150
200
500
800
1 000
落在“铅笔”
区域的次数m
68
111
136
345
564
701
落在“铅笔”
区域的频率
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
参考答案
1.【答案】B　2.【答案】D　3.【答案】A　4.【答案】15
5.【答案】(1)0.20;0.50;0.33　(2)0.33
解：随着试验次数的增加,频率会在某个数据附近摆动.
6.【答案】D
7.【答案】B　
解：由表中数据可知摸到白球的频率在0.8附近摆动,设白球有x个,则有0.8(10+x)=x,x=40.所以估计盒子里有40个白球.
8.【答案】B
9.解:(1)当n=1时,袋中红球数量和白球数量相同,故摸到两种颜色的球的可能性相同.
(2)由题意得0.25=,即(2+n)×0.25=1,所以n=2.　
10.解:(1)由题意可知,50次摸球试验中,出现红球20次,黄球30次,
所以红球占总球数的百分比约为20÷50=40%,
黄球占总球数的百分比约为30÷50=60%.
所以红球约占40%,黄球约占60%.
(2)由题意可知,50次摸球试验中,出现有记号的球4次,所以总球数约有8÷=100(个).
所以红球约有100×40%=40(个).
11.解:(1)如下表所示:
转动转盘的次数n
100
150
200
500
800
1 000
落在“铅笔”区域的次数m
68
111
136
345
564
701
落在“铅笔”区域的频率
0.68
0.74
0.68
0.69
0.705
0.701
(2)当n很大时,落在“铅笔”区域的频率将会接近0.7.
(3)获得铅笔的机会大.
(4)扇形的圆心角约是0.7×360°=252°.