第二章 相交线与平行线 达标检测卷

第二章 相交线与平行线 达标检测卷
题　号
一
二
三
总　分
得　分
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
一、选择题(每题3分,共30分)
1.在同一平面内两条直线的位置关系可能是(　　)
A.相交或垂直　　 B.垂直或平行
C.平行或相交 D.平行或相交或垂直
2.a,b,c是同一平面内任意三条直线,交点可能有(　　)
A.1个或2个或3个　 B.0个或1个或2个或3个
C.1个或2个　 D.都不对
3.如图,是同位角关系的是(　　)
A.∠3和∠4　　 B.∠1和∠4
C.∠2和∠4　　 D.不存在
4.下列语句叙述正确的有(　　)
①如果两个角有公共顶点且没有公共边,那么这两个角是对顶角;
②如果两个角相等,那么这两个角是对顶角;
③连接两点的线段长度叫做两点间的距离;
④直线外一点到这条直线的垂线段叫做这点到直线的距离.
A.0个　 B.1个　 C.2个　 D.3个
5.下列说法正确的是(　　)
A.两点之间的距离是两点间的线段
B.同一平面内,过一点有且只有一条直线与已知直线平行
C.与同一条直线垂直的两条直线也垂直
D.同一平面内,过一点有且只有一条直线与已知直线垂直
6.∠1和∠2是直线AB和CD被直线EF所截得到的同位角,那么∠1和∠2的大小关系是(　　)
A.∠1=∠2　　 B.∠1>∠2　　 C.∠1<∠2　　 D.无法确定
7.如图,有三条公路,其中AC与AB垂直,小明和小亮分别从A,B两点沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是(　　)21世纪教育网版权所有
A.小亮骑车的速度快
B.小明骑车的速度快
C.两人骑车的速度一样快
D.因为不知道公路的长度,所以无法判断他们骑车速度的快慢
8.下列说法中,正确的是(　　)
A.过点P不能画线段AB的垂线
B.P是直线AB外一点,Q是直线AB上一点,连接PQ,使PQ⊥AB
C.在同一平面内,过一点有且只有一条直线垂直于已知直线
D.过一点有且只有一条直线平行于已知直线
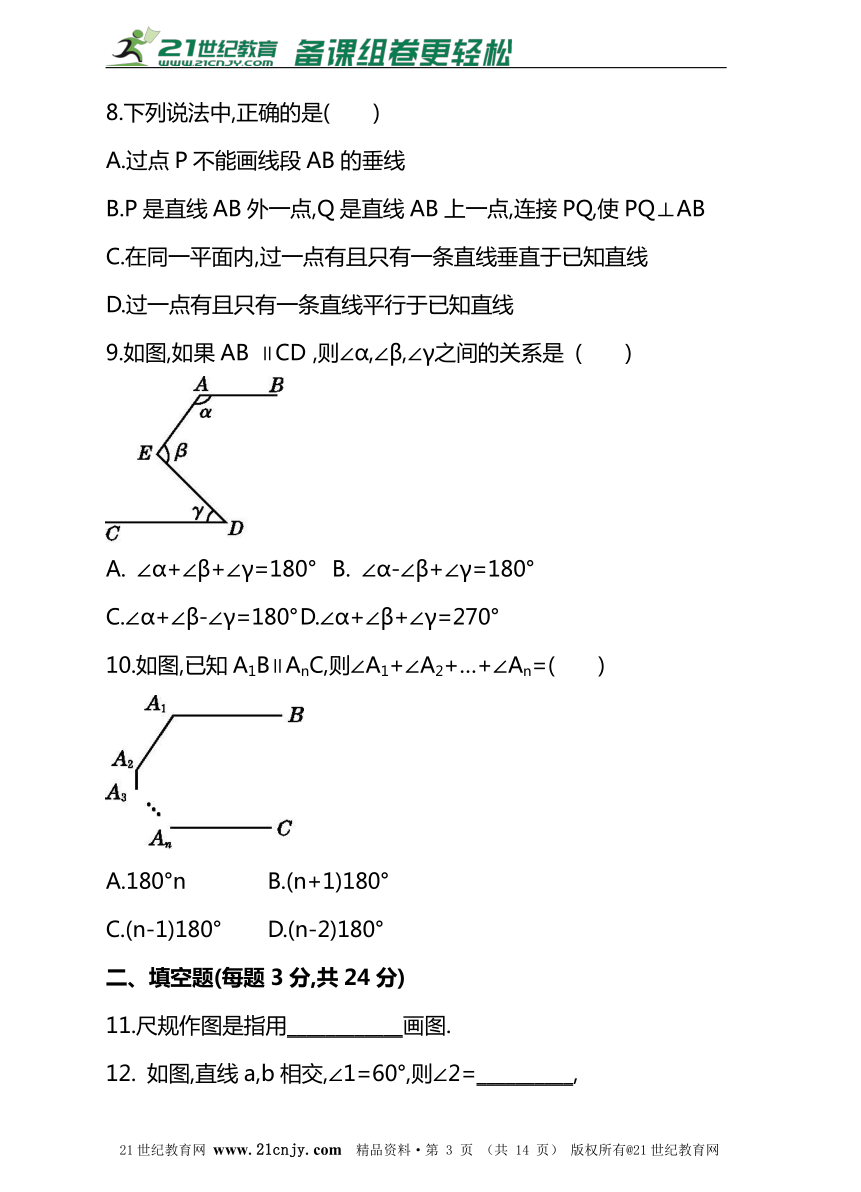
9.如图,如果AB ∥CD ,则∠α,∠β,∠γ之间的关系是 (　　)
A. ∠α+∠β+∠γ=180° B. ∠α-∠β+∠γ=180°
C.∠α+∠β-∠γ=180° D.∠α+∠β+∠γ=270°
10.如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An=(　　)
A.180°n　　　 B.(n+1)180°　　
C.(n-1)180°　　 D.(n-2)180°
二、填空题(每题3分,共24分)
11.尺规作图是指用____________画图.?
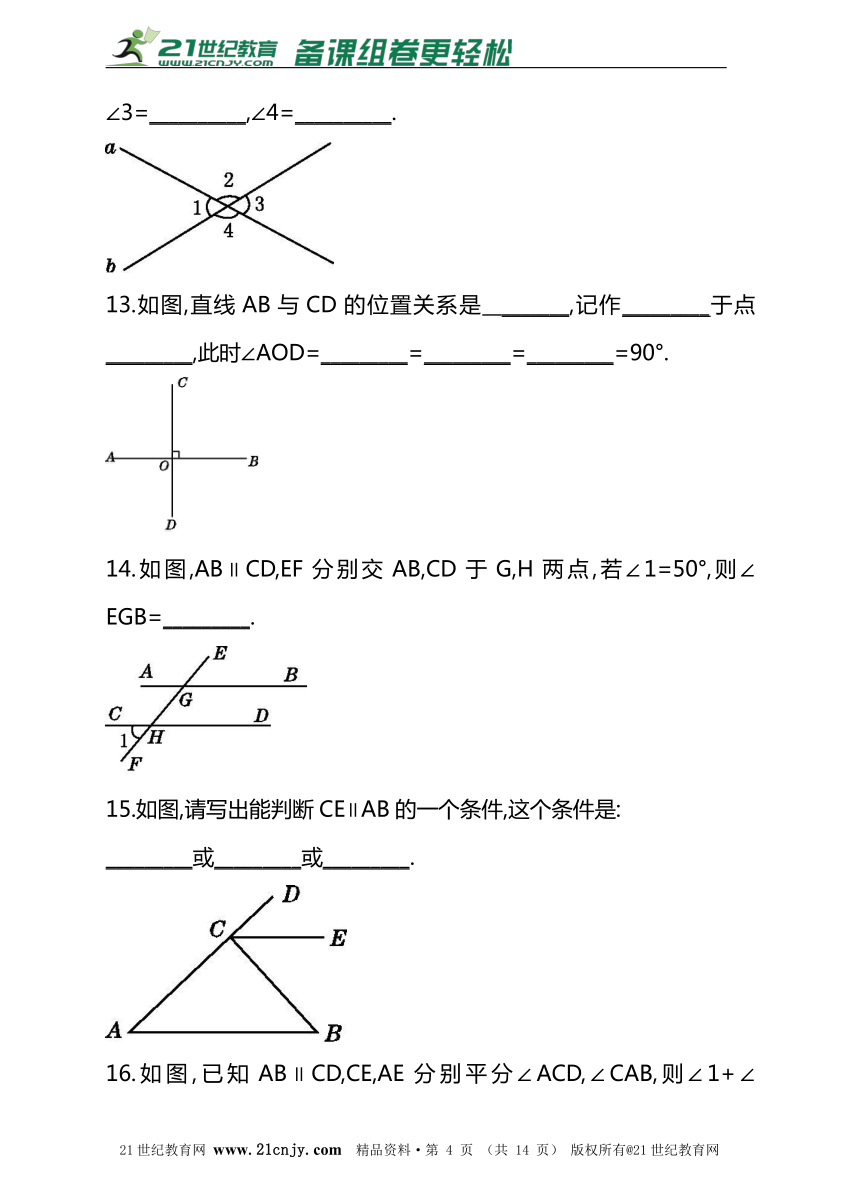
12. 如图,直线a,b相交,∠1=60°,则∠2=__________,
∠3=__________,∠4=__________.?
13.如图,直线AB与CD的位置关系是_________,记作_________于点_________,此时∠AOD=_________=_________=_________=90°.
?
14.如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=_________.21教育网
15.如图,请写出能判断CE∥AB的一个条件,这个条件是:
_________或_________或_________.
16.如图,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,则∠1+∠2=_________.21cnjy.com
17.同一平面内的三条直线a,b,c,若a⊥b,b⊥c,则a__________c.若a∥b,b∥c,则a_________c.若a∥b,b⊥c,则a_________c.?【来源：21·世纪·教育·网】
18.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西　　　　.21·世纪*教育网
三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)
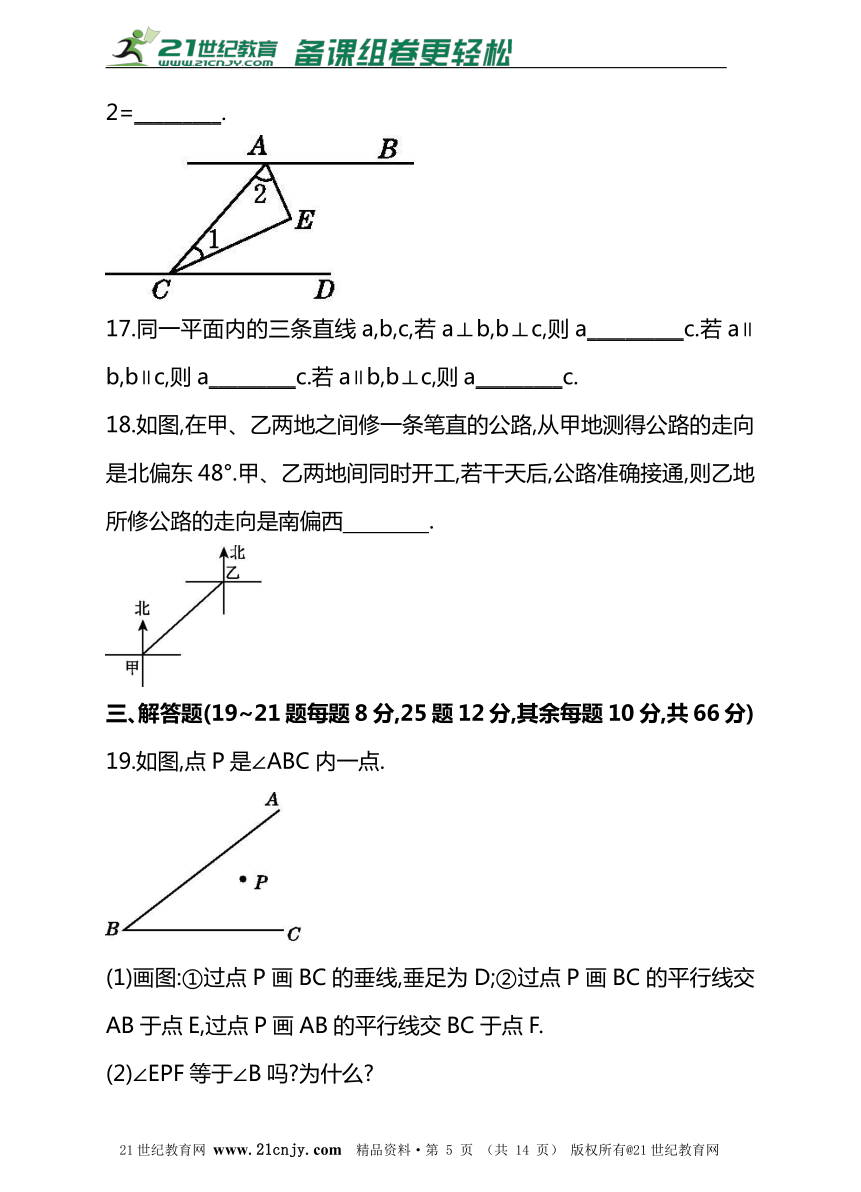
19.如图,点P是∠ABC内一点.
(1)画图:①过点P画BC的垂线,垂足为D;②过点P画BC的平行线交AB于点E,过点P画AB的平行线交BC于点F.www-2-1-cnjy-com
(2)∠EPF等于∠B吗?为什么?
(3)请你用直尺和圆规作图,作一个角,使它等于2∠ABC.(要求用尺规作图,不必写作法,但要保留作图痕迹)2-1-c-n-j-y
20.如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:21*cnjy*com
解:因为AD∥BC(已知),
所以∠1=∠3(___________).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥___________ (___________).?
所以∠3+∠4=180°(___________).
21.如图,已知∠1=∠2,AC平分∠DAB,你能判定哪两条直线平行?说明理由.
22.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)试说明:CF∥AB;
(2)求∠DFC的度数.
23.如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,求∠KOH的度数.
24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.试说明:AD∥BC.
25.如图,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB,∠PCD的关系,请你从所得关系中任意选取一个加以说明.
参考答案
一、1.【答案】C
2.【答案】B　
解：三条直线两两平行,没有交点;三条直线交于一点,有一个交点;两条直线平行与第三条直线相交,有两个交点;三条直线两两相交,不交于同一点,有三个交点,故选B.本题考查了相交线,分类讨论是解题关键,注意不要漏掉任何一种情况.www.21-cn-jy.com
3.【答案】B　
解：同位角的特征:在截线同旁,在两条被截直线同一方向上.
4.【答案】B　5.【答案】D
6.【答案】D　
解：因为不知道直线AB和CD是否平行,平行时同位角相等,不平行时同位角不相等,所以无法确定同位角的大小关系,故选D.
7.【答案】A
8.【答案】C　
解：过一点画线段的垂线,即过一点画线段所在直线的垂线,故A错误;P是直线AB外一点,Q是直线AB上一点,如果P点不在过Q点且与AB垂直的直线上,或Q点不在过P点且与AB垂直的直线上,连接PQ,不可能有PQ⊥AB,故B错误;过一点画直线的平行线,这点不能在直线上,否则是同一条直线,故D错误;故C正确.2·1·c·n·j·y
9.【答案】C　
解：如图,过点E向右作EF∥CD,则∠FED=∠γ;由AB∥CD,可知EF∥AB,所以∠α+∠AEF=180°,即∠AEF=180°-∠α.不难看出∠β=∠FED+∠AEF,由此得到∠β=∠γ+∠AEF=∠γ+180°-∠α,即【来源：21cnj*y.co*m】
∠α+∠β-∠γ=180°,故选C.
10.【答案】C　
解：如图,过点A2向右作A2D∥A1B,过点A3向右作A3E∥A1B,……
因为A1B∥AnC,
所以A3E∥A2D∥…∥A1B∥AnC,
所以∠A1+∠A1A2D=180°,∠DA2A3+∠A2A3E=180°,…,所以
∠A1+∠A1A2A3+…+∠An-1AnC=(n-1)180°.　
二、11.【答案】圆规和没有刻度的直尺
12. 【答案】120°;60°;120°
13.【答案】垂直;AB⊥CD; O;∠BOD; ∠BOC;∠AOC
14.【答案】50°　
解：因为AB∥CD,所以∠1=∠AGF.因为∠AGF与∠EGB是对顶角,所以∠EGB=∠AGF.故∠EGB=50°.【出处：21教育名师】
15.【答案】∠DCE=∠A;∠ECB=∠B;∠A+∠ACE=180°
16.【答案】90°　
解：因为AB∥CD,所以∠BAC+∠ACD=180°.因为CE,AE分别平分∠ACD,∠CAB,所以∠1+∠2=90°.【版权所有：21教育】
17.【答案】∥;∥;⊥
18.【答案】48°
三、19.解:(1)如图,①直线PD即为所求;②直线PE,PF即为所求.
(2)∠EPF=∠B.理由:因为PE∥BC(已知),所以∠AEP=∠B(两直线平行,同位角相等).又因为PF∥AB(已知),所以∠EPF=∠AEP(两直线平行,内错角相等),所以∠EPF=∠B(等量代换).21·cn·jy·com
(3)作∠MGH=∠ABC,以GH为一边在外侧再作∠HGN=∠ABC,即∠MGN=2∠ABC.
20.解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
21.解:DC∥AB,理由如下:
因为AC平分∠DAB,
所以∠1=∠3.
又因为∠1=∠2,
所以∠2=∠3.
所以DC∥AB(内错角相等,两直线平行).
22.解:(1)因为CF平分∠DCE,
所以∠1=∠2=∠DCE.
因为∠DCE=90°,
所以∠1=45°.
因为∠3=45°,
所以∠1=∠3.
所以CF∥AB(内错角相等,两直线平行).
(2)因为∠D=30°,∠1=45°,
所以∠DFC=180°-30°-45°=105°.
23.解:因为∠1+∠2=180°,
所以AB∥CD.
所以∠3=∠GOD.
因为∠3=100°,
所以∠GOD=100°.
所以∠DOH=180°-∠GOD=180°-100°=80°.
因为OK平分∠DOH,
所以∠KOH=∠DOH=×80°=40°.
24.解:因为AE平分∠BAD,
所以∠1=∠2.
因为AB∥CD,∠CFE=∠E,
所以∠1=∠CFE=∠E.
所以∠2=∠E.
所以AD∥BC.
25.解:题图①:∠APC+∠PAB+∠PCD=360°.
理由:过点P向右作PE∥AB,如图①,
因为AB∥CD,
所以AB∥PE∥CD.
所以∠A+∠1=180°,∠2+∠C=180°.
所以∠A+∠1+∠2+∠C=360°.
所以∠APC+∠PAB+∠PCD=360°.
题图②:∠APC=∠PAB+∠PCD.
理由:过点P向左作PE∥AB, 如图②,
因为AB∥CD,
所以AB∥PE∥CD.
所以∠1=∠A,∠2=∠C.
所以∠APC=∠1+∠2=∠PAB+∠PCD.
题图③:∠APC=∠PAB-∠PCD.理由: 延长BA交PC于E, 如图③,
因为AB∥CD,
所以∠1=∠C.
因为∠PAB=180°-∠PAE=∠1+∠P,
所以∠PAB=∠APC+∠PCD.
所以∠APC=∠PAB-∠PCD.
题图④:∠APC=∠PCD-∠PAB.理由:设AB与PC交于点Q,如图④,
因为AB∥CD,
所以∠1=∠C.
因为∠1=180°-∠PQA=∠A+∠P,
所以∠P=∠1-∠A.
所以∠APC=∠PCD-∠PAB.