第五章 生活中的轴对称 达标检测卷

第五章 生活中的轴对称 达标检测卷
题　号
一
二
三
总　分
得　分
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
一、选择题(每题3分,共30分)
1.下面所给的交通标志图中是轴对称图形的是(　　)
2.如图,两个“K”关于直线l成轴对称,则∠1的对应角为(　　)
A.∠4 B.∠5 C.∠6 D.∠3
3.下列说法中,正确的是(　　)
A.关于某直线对称的两个三角形是全等三角形
B.若两个三角形全等,则它们一定关于某直线对称
C.若两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
D.两个全等三角形对应点连线的垂直平分线就是它们的对称轴
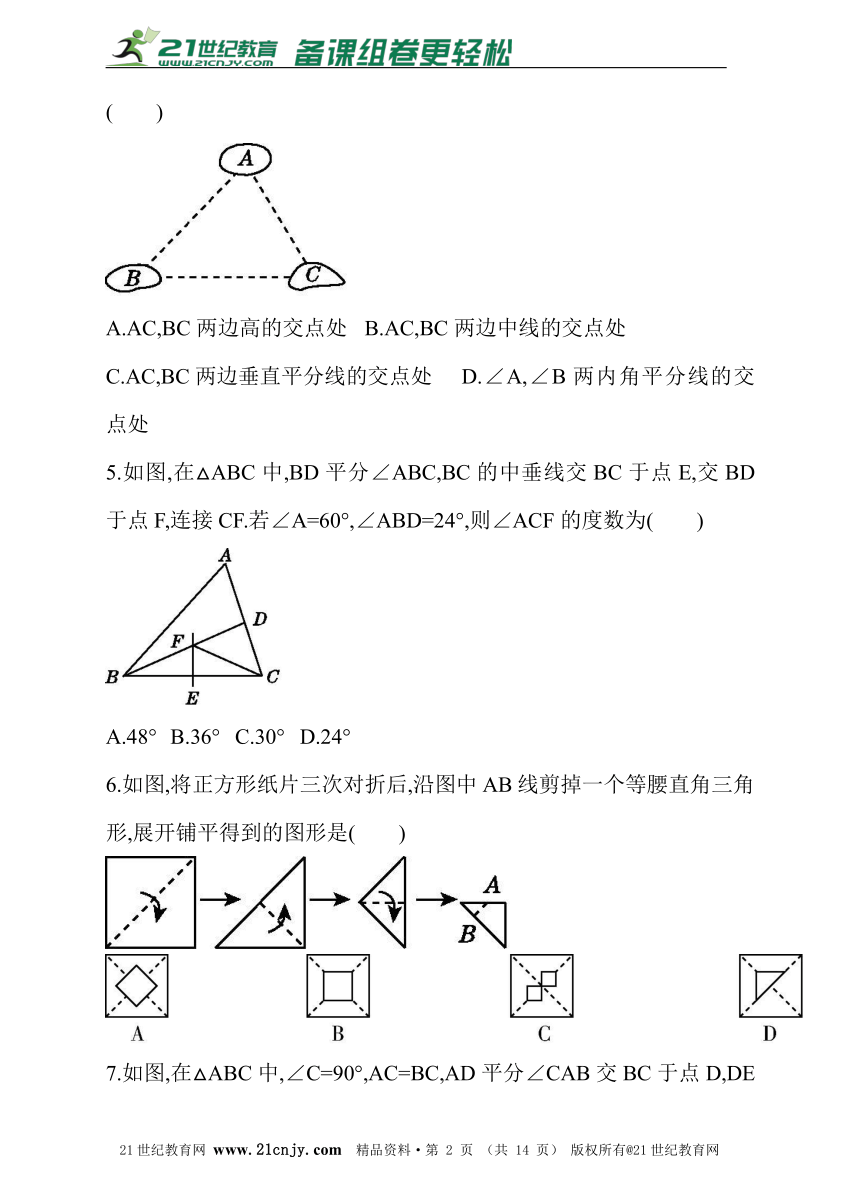
4.如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在(　　)www.21-cn-jy.com
A.AC,BC两边高的交点处 B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处 D.∠A,∠B两内角平分线的交点处
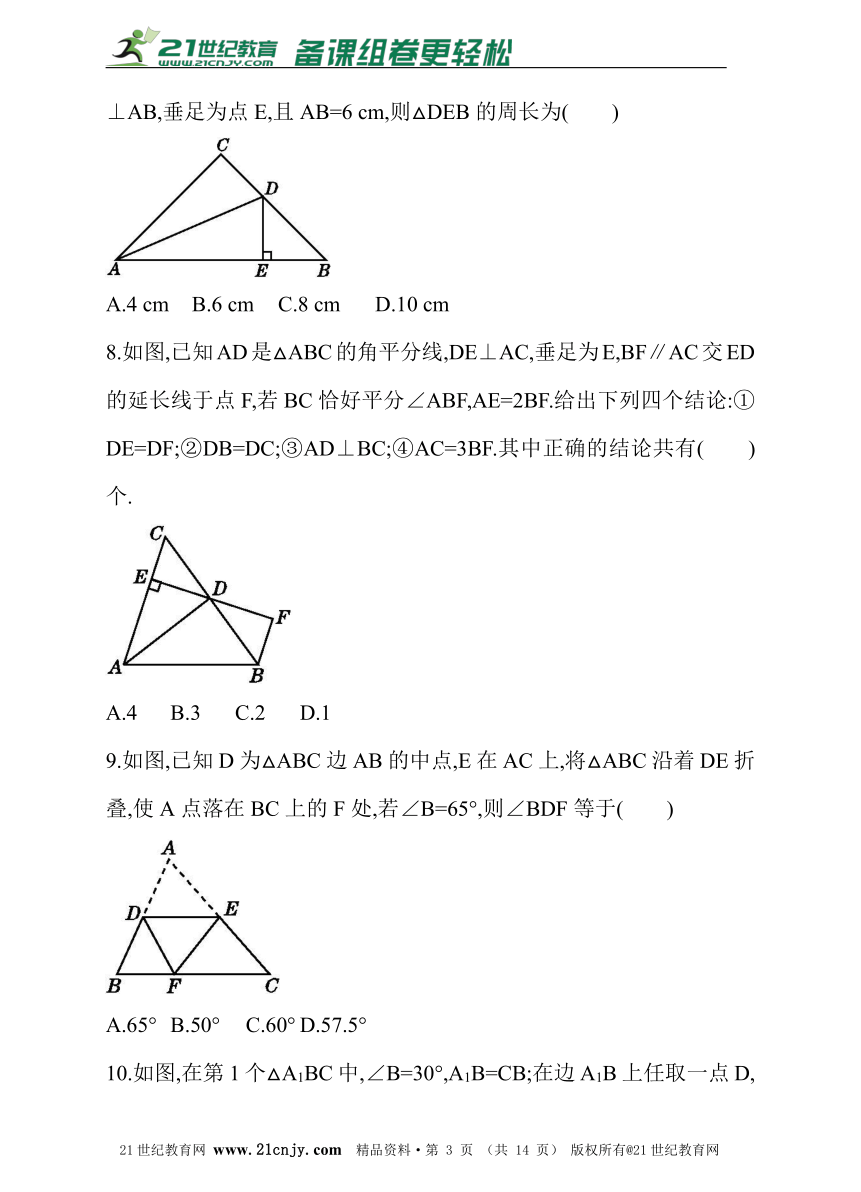
5.如图,在△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为(　　)
A.48° B.36° C.30° D.24°
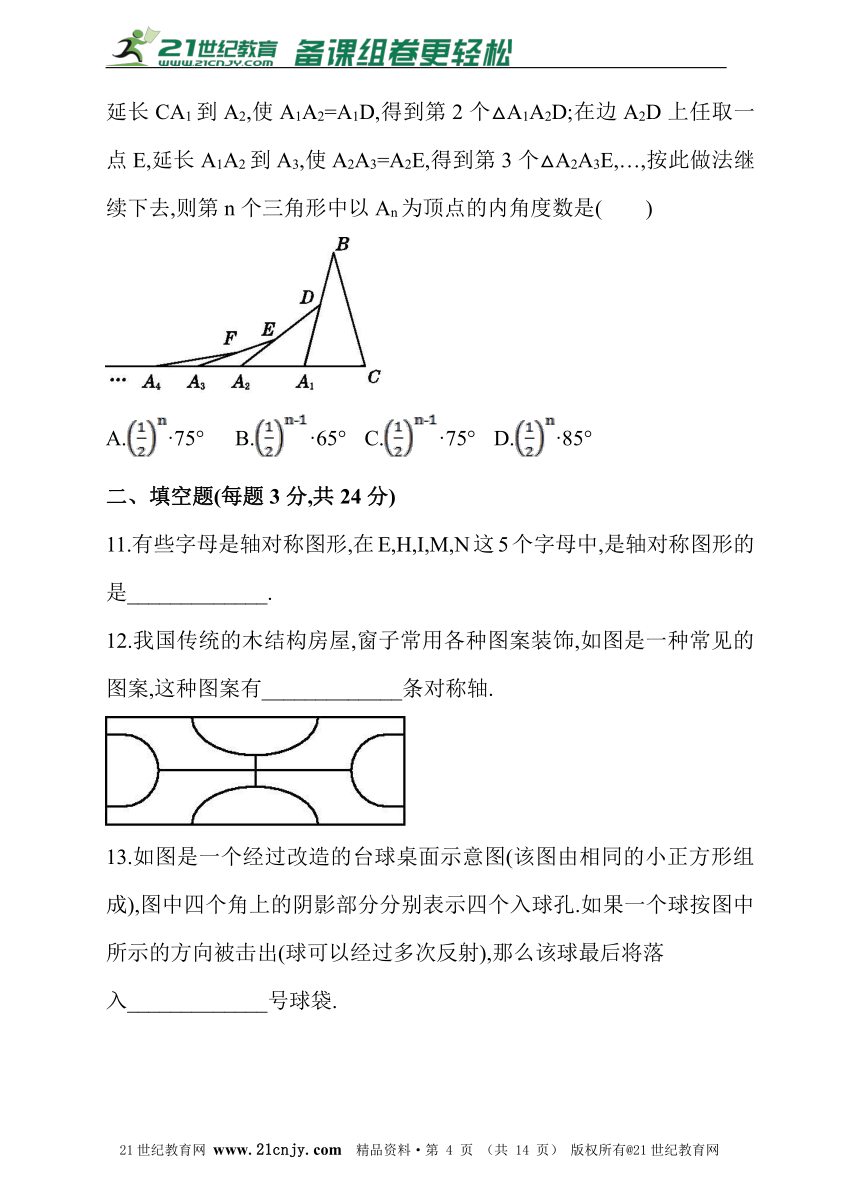
6.如图,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是(　　)
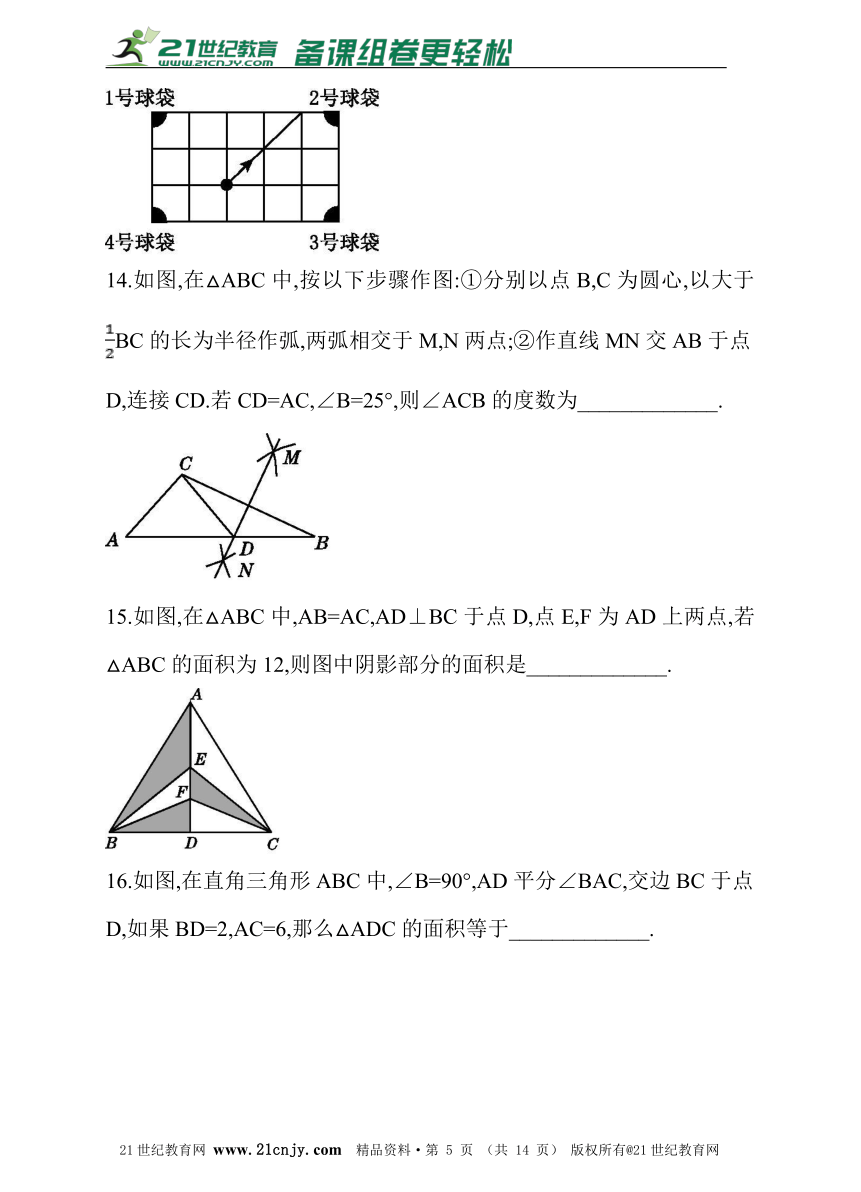
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为点E,且AB=6 cm,则△DEB的周长为(　　)
A.4 cm B.6 cm C.8 cm D.10 cm
8.如图,已知AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论共有(　　)个.21教育网
A.4 B.3 C.2 D.1
9.如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处,若∠B=65°,则∠BDF等于(　　)
A.65° B.50° C.60° D.57.5°
10.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…,按此做法继续下去,则第n个三角形中以An为顶点的内角度数是(　　)
A.·75° B.·65° C.·75° D.·85°
二、填空题(每题3分,共24分)
11.有些字母是轴对称图形,在E,H,I,M,N这5个字母中,是轴对称图形的是_____________. ?21·世纪*教育网
12.我国传统的木结构房屋,窗子常用各种图案装饰,如图是一种常见的图案,这种图案有_____________条对称轴.?www-2-1-cnjy-com
13.如图是一个经过改造的台球桌面示意图(该图由相同的小正方形组成),图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落
入_____________号球袋.?
14.如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为_____________.?
15.如图,在△ABC中,AB=AC,AD⊥BC于点D,点E,F为AD上两点,若△ABC的面积为12,则图中阴影部分的面积是_____________.?
16.如图,在直角三角形ABC中,∠B=90°,AD平分∠BAC,交边BC于点D,如果BD=2,AC=6,那么△ADC的面积等于_____________.?
17.如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC=_____________.　2-1-c-n-j-y
18.小威在计算时发现:11×11=121,111×111=12321,1111×1111=1234 321,…,他从中发现了一个规律.请根据他所发现的规律很快地写出111111111×111111111=_____________.?【出处：21教育名师】
三、解答题(19题8分,20~21题每题10分,24题14分,其余每题12分,共66分)
19.如图是由边长为1的小正方形组成的网格,在网格中画了一个“小猪”的图案.
(1)“小猪”所占的面积为____________;?
(2)在网格中作出“小猪”关于直线DE对称的图案(只画图,不写作法).
20.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)21教育名师原创作品
21.如图,在等边三角形ABC中,∠ABC,∠ACB的平分线相交于点O,作BO,CO的垂直平分线分别交BC于点E和点F.小明说:“E,F是BC的三等分点.”你同意他的说法吗?请说明理由.21·cn·jy·com
22.如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE.
试说明:(1)△AEF≌△CEB;(2)∠ABF=2∠FBD.
23.操作与探究.
(1)分别画出图①中“”和“”关于直线l的对称图形(画出示意图即可).
(2)图②中小冬和小亮上衣上印的字母分别是什么?
(3)把字母“”和“”写在薄纸上,观察纸的背面,写出你看到的字母背影.
(4)小明站在五个学生的身后,这五个学生正向前方某人用手势示意一个五位数,从小明站的地方看(如图③所示),这个五位数是23456.请你判断出他们示意的真实五位数是多少?21*cnjy*com
24.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD=_________°,∠DEC=_________°,点D从B向C运动时,∠BDA逐渐变_________ (填“大”或“小”).?
(2)当DC等于多少时,△ABD≌DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形的情形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.
参考答案
一、1.【答案】A
2.【答案】A　
解：由轴对称的性质知,∠1的对应角为∠4.故选A.
3.【答案】A　4.【答案】C　5.【答案】A　6.【答案】A
7.【答案】B　
解：先利用AAS判定△ACD≌△AED,得出AC=AE,CD=ED,再对构成△DEB的几条边进行变换,可得到其周长等于AB的长.
8.【答案】A　
解：因为BF∥AC,所以∠C=∠CBF.因为BC平分∠ABF,所以∠ABC=∠CBF.所以∠C=∠ABC.所以AB=AC.因为AD是△ABC的角平分线,所以BD=CD,AD⊥BC.故②③正确.21世纪教育网版权所有
在△CDE与△BDF中,
所以△CDE≌△BDF.所以DE=DF,CE=BF.故①正确;
因为AE=2BF,所以AC=3BF.故④正确.故选A.
9.【答案】B　
解：因为△DEF是由△DEA沿直线DE翻折变换而来,所以AD=DF.因为D是AB边的中点,所以AD=BD.所以BD=DF.所以∠B=∠BFD.因为∠B=65°,所以∠BDF=180°-∠B-∠BFD=180°-65°-65°=50°.故选B.
10.【答案】C
二、11.【答案】E,H,I,M　12.【答案】2
13.【答案】1　
解：如图,该球最后将落入1号球袋.
14.【答案】105°
15.【答案】6　
解：因为AB=AC,AD⊥BC,所以△ABC关于直线AD对称.所以S△BEF=S△CEF.因为△ABC的面积为12,所以图中阴影部分的面积=S△ABC=6.21cnjy.com
16.【答案】6　
解：过点D作DE⊥AC于点E,因为AD平分∠BAC,所以DE=BD=2.所以S△ADC=AC·DE=×6×2=6.21*cnjy*com
17.【答案】108°　
解：连接OB,OC.因为∠BAC=54°,AO为∠BAC的平分线,所以∠BAO=∠BAC=27°.【版权所有：21教育】
又因为AB=AC,所以∠ABC=(180°-∠BAC)=×(180°-54°)=63°.因为DO是AB的垂直平分线,
所以OA=OB.所以∠ABO=∠BAO=27°.
所以∠OBC=∠ABC-∠ABO=63°-27°=36°.
因为AB=AC,AO为∠BAC的平分线,
所以AO所在直线是BC的垂直平分线.所以OB=OC.
所以∠OCB=∠OBC=36°.因为将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,所以OE=CE.所以∠COE=∠OCB=36°.在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.【来源：21cnj*y.co*m】
18.【答案】12 345 678 987 654 321
三、19.解:(1)32.5
(2)如图所示:
20.解:如图.点C1,C2即为所求作的点.
21.解:同意.理由如下:
如图,连接OE,OF.由题意,知BE=OE,CF=OF,∠OBC=∠OCB=30°,
所以∠BOE=∠OBC,∠COF=∠OCB,∠BOC=120°.
所以∠EOF=60°,∠OEF=60°,∠OFE=60°.
所以△OEF是等边三角形.
所以OE=OF=EF=BE=CF.
所以E,F是BC的三等分点.
22.解:(1)因为AD⊥BC,CE⊥AB,所以∠AEF=∠CEB=90°,
∠AFE+∠EAF=90°,∠CFD+∠ECB=90°.
又因为∠AFE=∠CFD,所以∠EAF=∠ECB.
在△AEF和△CEB中,
因为∠AEF=∠CEB,AE=CE,∠EAF=∠ECB,
所以△AEF≌△CEB.
(2)由△AEF≌△CEB,得EF=EB,
所以∠EBF=∠EFB.
在△ABC中,AB=AC,AD⊥BC,
所以BD=CD.所以∠FBD=∠FCD.
因为∠EFB=180°-∠BFC=∠FBD+∠FCD=2∠FBD,
所以∠EBF=2∠FBD,
即∠ABF=2∠FBD.
23.解:(1)图略.(2)“”和“”.
(3)“”和“”.
(4)他们示意的真实五位数是42635,如图.
解：从身后看到的手势旋转180°,排尾变排头,实际上是从身后看到的手势关于直线l的对称手势,如图所示,即为从身前看到的手势,所以是42635.2·1·c·n·j·y
24.解:(1)25;115;小
(2)当DC=2时,△ABD≌△DCE.
理由如下:
因为DC=2,AB=2,所以DC=AB.
因为AB=AC,∠B=40°,
所以∠B=∠C=40°.
因为∠ADB=180°-∠ADC=∠DAC+∠C,∠DEC=180°-∠AED=∠DAC+∠ADE,且∠C=40°,∠ADE=40°,【来源：21·世纪·教育·网】
所以∠ADB=∠DEC.
在△ADB与△DEC中,
∠ADB=∠DEC,∠B=∠C,AB=DC,
所以△ABD≌△DCE.
(3)存在,∠BDA=110°或∠BDA=80°.