苏科版八年级下《10.3分式的加减》同步练习含详细答案
文档属性
| 名称 | 苏科版八年级下《10.3分式的加减》同步练习含详细答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-02 00:00:00 | ||
图片预览
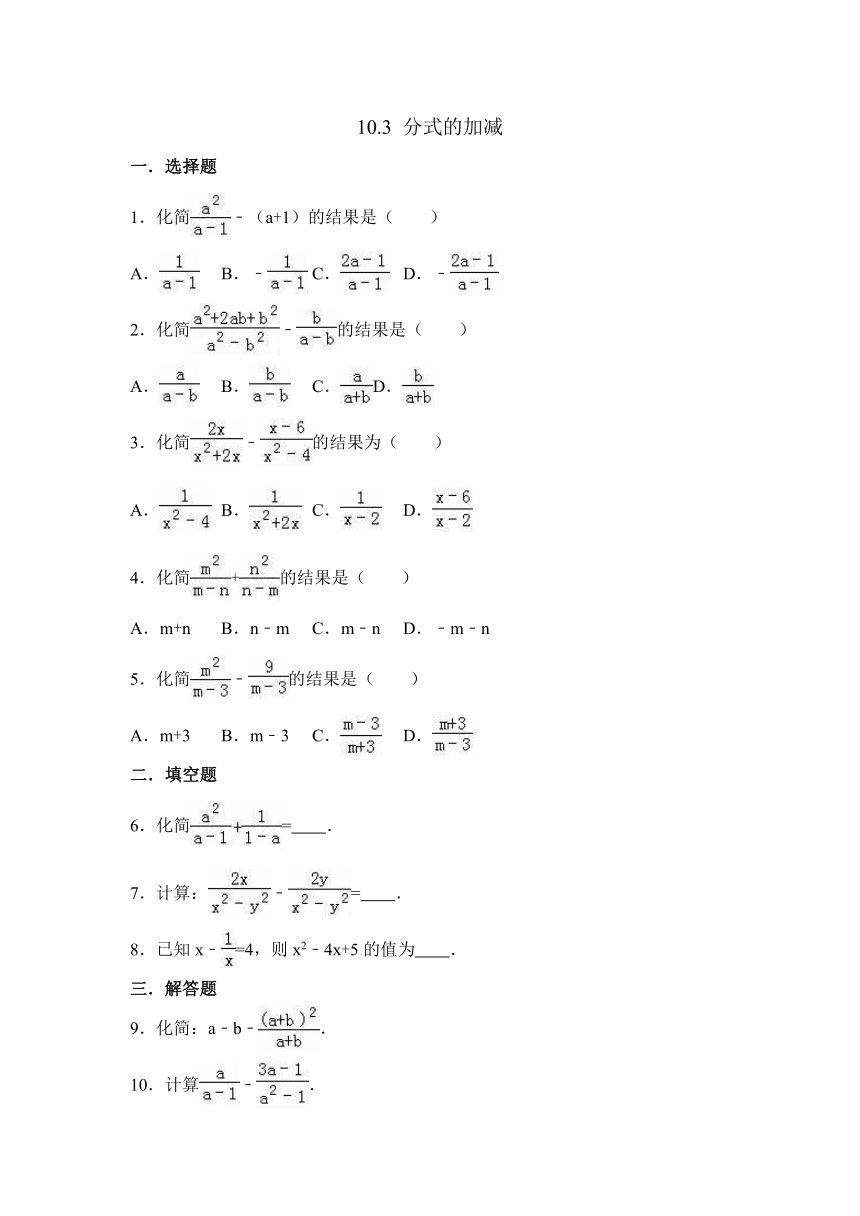


文档简介
10.3
分式的加减
一.选择题
1.化简﹣(a+1)的结果是( )
A.
B.﹣
C.
D.﹣
2.化简﹣的结果是( )
A.
B.
C.
D.
3.化简﹣的结果为( )
A.
B.
C.
D.
4.化简+的结果是( )
A.m+n
B.n﹣m
C.m﹣n
D.﹣m﹣n
5.化简﹣的结果是( )
A.m+3
B.m﹣3
C.
D.
二.填空题
6.化简= .
7.计算:﹣= .
8.已知x﹣=4,则x2﹣4x+5的值为 .
三.解答题
9.化简:a﹣b﹣.
10.计算﹣.
11.化简:.
12.化简:
+.
答案与解析
一.选择题
1.(2016 绥化)化简﹣(a+1)的结果是( )
A.
B.﹣
C.
D.﹣
【分析】先根据通分法则把原式变形,再根据平方差公式、合并同类项法则计算即可.
【解答】解:原式=﹣
=,
故选:A.
【点评】本题考查的是分式的加减法,掌握分式的加减法法则、平方差公式是解题的关键.
2.(2015 山西)化简﹣的结果是( )
A.
B.
C.
D.
【分析】原式第一项约分后,利用同分母分式的减法法则计算,即可得到结果.
【解答】解:原式=﹣
=﹣
=
=,
故选A.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
3.(2015 百色)化简﹣的结果为( )
A.
B.
C.
D.
【分析】先通分,再把分子相加减即可.
【解答】解:原式=﹣
=
=
=
=.
故选C.
【点评】本题考查的是分式的加减法,熟知异分母分式的加减法法则是解答此题的关键.
4.(2016 攀枝花)化简+的结果是( )
A.m+n
B.n﹣m
C.m﹣n
D.﹣m﹣n
【分析】首先进行通分运算,进而分解因式化简求出答案.
【解答】解:
+
=﹣
=
=m+n.
故选:A.
【点评】此题主要考查了分式的加减运算,正确分解因式是解题关键.
5.(2015 济南)化简﹣的结果是( )
A.m+3
B.m﹣3
C.
D.
【分析】原式利用同分母分式的减法法则计算,约分即可得到结果.
【解答】解:原式===m+3.
故选A.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
二.填空题(共9小题)
6.(2016 临沂)化简= a+1 .
【分析】首先把两个分式的分母变为相同再计算.
【解答】解:原式=﹣=a+1.
故答案为:a+1.
【点评】此题考查的知识点是分式的加减法,关键是先把两个分式的分母化为相同再计算.
7.(2016 昆明)计算:﹣= .
【分析】同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减;再分解因式约分计算即可求解.
【解答】解:﹣
=
=
=.
故答案为:.
【点评】考查了分式的加减法,注意通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.
8.(2016 德阳)已知x﹣=4,则x2﹣4x+5的值为 6 .
【分析】首先根据x﹣=4,求出x2﹣4x的值是多少,然后把求出的x2﹣4x的值代入x2﹣4x+5,求出算式的值是多少即可.
【解答】解:∵x﹣=4,
∴x2﹣1=4x,
∴x2﹣4x=1,
∴x2﹣4x+5=1+5=6.
故答案为:6.
【点评】此题主要考查了分式的加减法,要熟练掌握,注意代入法的应用.
三.解答题(共10小题)
9.(2016 福州)化简:a﹣b﹣.
【分析】先约分,再去括号,最后合并同类项即可.
【解答】解:原式=a﹣b﹣(a+b)
=a﹣b﹣a﹣b
=﹣2b.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
10.(2016 南京)计算﹣.
【分析】首先进行通分运算,进而合并分子,进而化简求出答案.
【解答】解:﹣
=﹣
=
=
分式的加减
一.选择题
1.化简﹣(a+1)的结果是( )
A.
B.﹣
C.
D.﹣
2.化简﹣的结果是( )
A.
B.
C.
D.
3.化简﹣的结果为( )
A.
B.
C.
D.
4.化简+的结果是( )
A.m+n
B.n﹣m
C.m﹣n
D.﹣m﹣n
5.化简﹣的结果是( )
A.m+3
B.m﹣3
C.
D.
二.填空题
6.化简= .
7.计算:﹣= .
8.已知x﹣=4,则x2﹣4x+5的值为 .
三.解答题
9.化简:a﹣b﹣.
10.计算﹣.
11.化简:.
12.化简:
+.
答案与解析
一.选择题
1.(2016 绥化)化简﹣(a+1)的结果是( )
A.
B.﹣
C.
D.﹣
【分析】先根据通分法则把原式变形,再根据平方差公式、合并同类项法则计算即可.
【解答】解:原式=﹣
=,
故选:A.
【点评】本题考查的是分式的加减法,掌握分式的加减法法则、平方差公式是解题的关键.
2.(2015 山西)化简﹣的结果是( )
A.
B.
C.
D.
【分析】原式第一项约分后,利用同分母分式的减法法则计算,即可得到结果.
【解答】解:原式=﹣
=﹣
=
=,
故选A.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
3.(2015 百色)化简﹣的结果为( )
A.
B.
C.
D.
【分析】先通分,再把分子相加减即可.
【解答】解:原式=﹣
=
=
=
=.
故选C.
【点评】本题考查的是分式的加减法,熟知异分母分式的加减法法则是解答此题的关键.
4.(2016 攀枝花)化简+的结果是( )
A.m+n
B.n﹣m
C.m﹣n
D.﹣m﹣n
【分析】首先进行通分运算,进而分解因式化简求出答案.
【解答】解:
+
=﹣
=
=m+n.
故选:A.
【点评】此题主要考查了分式的加减运算,正确分解因式是解题关键.
5.(2015 济南)化简﹣的结果是( )
A.m+3
B.m﹣3
C.
D.
【分析】原式利用同分母分式的减法法则计算,约分即可得到结果.
【解答】解:原式===m+3.
故选A.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
二.填空题(共9小题)
6.(2016 临沂)化简= a+1 .
【分析】首先把两个分式的分母变为相同再计算.
【解答】解:原式=﹣=a+1.
故答案为:a+1.
【点评】此题考查的知识点是分式的加减法,关键是先把两个分式的分母化为相同再计算.
7.(2016 昆明)计算:﹣= .
【分析】同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减;再分解因式约分计算即可求解.
【解答】解:﹣
=
=
=.
故答案为:.
【点评】考查了分式的加减法,注意通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.
8.(2016 德阳)已知x﹣=4,则x2﹣4x+5的值为 6 .
【分析】首先根据x﹣=4,求出x2﹣4x的值是多少,然后把求出的x2﹣4x的值代入x2﹣4x+5,求出算式的值是多少即可.
【解答】解:∵x﹣=4,
∴x2﹣1=4x,
∴x2﹣4x=1,
∴x2﹣4x+5=1+5=6.
故答案为:6.
【点评】此题主要考查了分式的加减法,要熟练掌握,注意代入法的应用.
三.解答题(共10小题)
9.(2016 福州)化简:a﹣b﹣.
【分析】先约分,再去括号,最后合并同类项即可.
【解答】解:原式=a﹣b﹣(a+b)
=a﹣b﹣a﹣b
=﹣2b.
【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
10.(2016 南京)计算﹣.
【分析】首先进行通分运算,进而合并分子,进而化简求出答案.
【解答】解:﹣
=﹣
=
=
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
